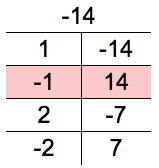3.1 考虑二次曲线表达式-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 计算二次曲线表达式

  Collapse Expand

  计算二次曲线表达式

  播放段落

  Lesson Objectives
  ::经验教训目标

  播放段落
  • Factor quadratics using the area model and  the decomposition method.
    ::使用区域模型和分解法的因子二次方位。
  播放段落
  • Factor difference of squares  and perfect square trinomials.
    ::方形和完美的方形三角形的因数差异。

  ---

  播放段落

  Introduction: What is Factoring?
  ::导言:什么是保理?

  

  播放段落

  What could the respective lengths and widths be of images 1, 2, and 3?
  ::图像1、2和3的长度和宽度如何?

  播放段落

  The process of factoring involves breaking up a number, term , polynomial , or expression into parts which, when multiplied, will produce the original expression . D ivision with was first explored in when one factor of a polynomial was used to rewrite a polynomial as the product of its factors. Factors can take the form of a number, a variable , or an expression. Here are the factorizations of the rectangles above:
  ::保理过程包括将一个数字、术语、多义或表达式拆分成部分,这些部分在乘以后将产生原始表达式。当使用一个多义因子来重写一个多义因子作为其因子的产物时,首次探索了该除法。 系数可以采取数字、变量或表达式的形式。 下面是上述矩形的因数:

  1. $\begin{align*}60 = 2 \cdot 2 \cdot 3 \cdot 5\end{align*}$  
  播放段落
  2. $\begin{align*}3x^2y = 3 \cdot x \cdot x \cdot y\end{align*}$  
     ::3x2y=3xxxx
  播放段落
  3. $\begin{align*}x^2 - 3x - 10 = (x + 2) \cdot (x - 5)\end{align*}$  
     ::x2-3x-10=(x+2)__(x-5)

  播放段落

  T hese simple factors can be arranged in any combination. For example, rectangle 1 could be 4 ft. by 15 ft. or 12 ft. by 5 ft. Rectangle 2 could be 3 ft. by  $\begin{align*}x^2y\end{align*}$  ft. or  $\begin{align*}3x\end{align*}$  ft. by  $\begin{align*}xy\end{align*}$  ft.
  ::这些简单因素可以通过任何组合排列。例如,矩形1可以是4英尺乘15英尺或12英尺乘5英尺。矩形2可以是3英尺乘x2英尺或3英尺乘x3英尺。

   

  播放段落

  The use of factoring in the real world is especially common when working with quadratics, which are often used to model acceleration, curved paths, and area models. Arguably, the most important application of involves the zero property which will be explored in Roots of Quadratic Functions . Let’s begin with a review of some of the factoring techniques learned in Algebra 1.
  ::在现实世界中,使用保理学在与经常用来模拟加速、弯曲路径和区域模型的象形体合作时,在现实世界中特别常见。 可以说,最重要的应用涉及将在“四边函数根”中探索的零属性。 让我们首先审查代数1中学到的一些保理技术。

   

  ---

  播放段落

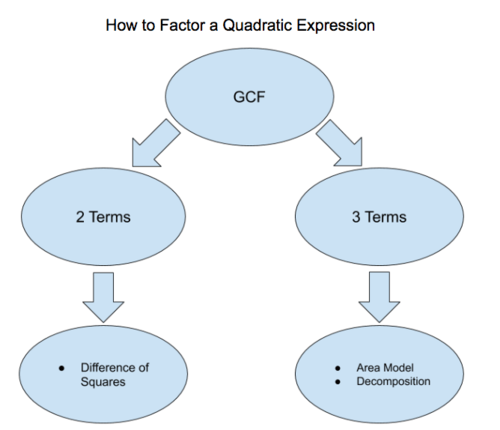
  Activity 1: Greatest Common Factor
  ::活动1:最大共同因素

  播放段落

  In the section Functions, the parent function $\begin{align*}f(x) = x^2.\end{align*}$ was introduced. In this section, quadratic functions and expressions will be explored. A quadratic function is a second- degree polynomial function that can be written in the form  $\begin{align*}ax^2 + bx + c.\end{align*}$   This form is known as the standard form . The coefficients $\begin{align*}a, b,\end{align*}$   and $\begin{align*}c\end{align*}$   are important as each coefficient has a specific effect on the function. The coefficient of the  $\begin{align*}x^2\end{align*}$  term is called the $\begin{align*}a\end{align*}$  -coefficient, the coefficient of the $\begin{align*}x\end{align*}$   term is called the $\begin{align*}b\end{align*}$  -coefficient, and the constant is called the $\begin{align*}c\end{align*}$  -coefficient. Even though the $\begin{align*}c\end{align*}$   term is a constant, it is called a coefficient because it is is often thought of  $\begin{align*}cx^0.\end{align*}$
  ::函数节中引入了父函数 f( x) =x2. 。 在本节中, 将探索二次函数和表达式。 二次函数是第二度多角度函数, 可以以 x2+bx+c 的形式写成。 这个形式被称为标准形式。 系数a、 b 和 c 很重要, 因为每个系数都对函数有特定影响。 x2 术语的系数被称为 - 系数, x 术语的系数被称为 b - 系数, 常数被称为 c - 系数。 尽管 c 术语是一个常数, 但它也被称为系数, 因为常被认为是 cx0 。

  播放段落

  When factoring a quadratic expression, you are attempting to find the expressions that when multiplied together will produce the quadratic. When a quadratic is written as a product of its factors, this is known as the  factored form . The first thing you should attempt is to factor out the greatest common factor . Factoring out the greatest common factor is the reverse of the . Rather than multiplying every term of a polynomial by a factor, every term is being divided by a factor. T he result of the division is then written as the product of the removed factor and left-over expression.
  ::当乘以二次表达式时,您正在试图找到当相乘后将产生二次表达式的表达式。 当二次表达式被写成其因子的产物时, 这被称为因子表达式。 首先, 您应该尝试将最大共同因素考虑在内。 乘以最大共同因素是反向的。 计算最大共同因素时, 而不是将多式表达式的每个术语乘以一个系数, 每个术语都被除以一个系数。 然后, 分割的结果被写成被删除的因子和剩余表达式的产物 。

   

  

  播放段落

  Use the interactive below to review factoring out a greatest common factor.
  ::利用以下互动方式审查考虑一个最大的共同因素。

   

   

   

  ---

  播放段落

  Activity 2: Factoring Quadratics
  ::活动2:保理四方

  播放段落

  After dividing out the greatest common factor, if there is one, the next step is to find the binomials that will multiply to the quadratic. In Multiplying Polynomials, the area model was used to represent the product of two binomials. T his same model can be used to get from a product to the two factors that produced it.
  ::在分离了最大共同因素之后, 如果存在一个, 下一步就是找到会乘以四角的二进制。 在倍增多式多面体中, 区域模型被用来代表两个二进制的产物。 同样的模型可以用来从一个产品到产生它的两个因素。

   

   

   

  播放段落

  Example
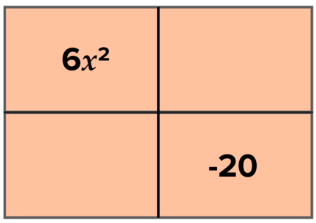
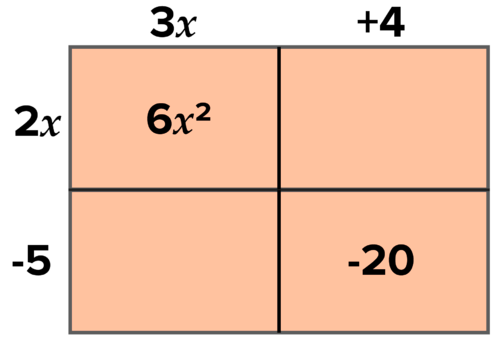
  ::示例示例示例示例

  播放段落

  Use the area model to factor  $\begin{align*}6x^2 − 7x − 20.\end{align*}$
  ::将区域模型用于乘数 6x2-7x-20。

  播放段落

  When using the area model to factor a trinomial to the product two binomials, draw a rectangle divided into 4 boxes. The value of the top left box is the leading term, and the value of the bottom right box is the constant term. 
  ::当使用区域模型对产品两个二进制乘以三进制时,请绘制一个矩形,分为4个框。左上方框的值为前题,右下方框的值为常数。

  

  播放段落

  The options for the dimensions of the top-left box are the factors of  $\begin{align*}6x^2.\end{align*}$   Some experimentation is required, so choose two factors, say,  $\begin{align*}2x\end{align*}$   and  $\begin{align*}3x.\end{align*}$  The options for the dimensions of the bottom right box are the factors of −20. These dimensions are written on the right side of the top and on the bottom of the left side. Some experimentation is required, so choose two factors, say −5 and 4. Write these values as the dimensions of the bottom left box:
  ::左上方框的维度选项是 6x2 的因数。 需要做一些实验, 请选择两个因数, 例如 2x 和 3x。 右下方框的维度选项是 -20 的因数。 这些维度写在上方的右侧和左侧的底部。 需要做一些实验, 请选择两个因数, 比如 -5 和 4. 。 将这些值写为左下方框的维度 :

  

  播放段落

  Now find the areas of the unknown regions by multiplying the dimensions directly above and to the left of each box: 
  ::现在通过将每个框的上方和左侧的维度乘以未知区域的区域 来找到未知区域的区域 :

  

  播放段落

  The sum of the areas of the regions is  $\begin{align*}6x^2 − 7x − 20.\end{align*}$   This  expression is the quadratic that you were seeking to factor. Writing the area above as the product of the dimensions give the answer.
  ::区域面积的总和是 6x2 - 7x - 20。 这个表达式是您想要考虑的二次方块 。 将以上区域写成尺寸的产物给出答案 。

  播放段落

  Answer:  $\begin{align*}6x^2−7x−20 = (2x − 5)(3x + 4)\end{align*}$
  ::答复: 6x2-7x-20=(2x-5)(3x+4)

  播放段落

  Teacher's Note: Using an area model is a visual representation of the commonly used guess and check method.
  ::教师说明:使用区域模型是常见的猜测和检查方法的直观表示。

  播放段落

  Using the area model to factor requires experimentation. The quadratic and linear terms of a quadratic can have many factors, and they can be placed in different locations on the perimeter of the rectangle. The process requires testing and eliminating factors that do not work.
  ::使用区域模型作为因子需要实验。二次方的二次和线性术语可以有许多因素,可以放在矩形周围的不同地点。这一过程需要测试和消除不起作用的因素。

   

   

   

  ---

  播放段落

  Extension: Algebra Tiles
  ::扩展名:代数平铺

  播放段落

  Algebra tiles are a great way to visualize factoring a quadratic. Use the interactive below to explore this idea.
  ::代数瓦是可视化二次方位乘数的好方法。 使用下面的互动来探索这个想法 。

   

   

   

  ---

  播放段落

  Activity 3: Decomposition
  ::活动3:分解

  播放段落

  It is no coincidence that the method above is based on reversing the multiplication that would have produced the quadratic expression. Many of the methods for factoring quadratics are based on reversing multiplication. The next method, known as decomposition, is the reverse of distribution. Distribution  as a method for multiplying polynomials was discussed in the section  Multiplying Polynomials :
  ::上述方法以扭转本可产生二次表达式的乘数为基础,这绝非巧合。许多计算二次表达式的乘数方法以逆向乘数为基础。下一个方法,即分解法,是分布的反向。多面性多面性部分讨论了作为多面性乘数方法的分布:

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Multiply  $\begin{align*}(x-3)(2x-5)\end{align*}$
  ::乘(x-3)(2x-5)

  播放段落

  Step 1: Distribute the first term to each term in the second polynomial.
  ::第1步:将第一个任期分配到第二个多年度的每个任期。

  播放段落

  $$\begin{align*}(x-3)(2x-5) = (x-3) \cdot 2x + (x-3) \cdot -5\end{align*}$$
  :x-3)(2x-5)=(x-3)2x+(x-3)5

  播放段落

  Step 2: Distribute the monomial factor to each respective binomial .
  ::第2步:将单一因数分配到各自的二元因数。

  播放段落

  $$\begin{align*}(x-3) \cdot 2x + (x-3) \cdot -5 &= x \cdot 2x + -3 \cdot 2x + x \cdot -5 + -3 \cdot -5 \\ &= 2x^2 - 6x + -5x + 15\end{align*}$$
  :x3)%2x+(x3) @%5=x2x @%3}%2x+x=5*5*3**5*5=2x2-6x=5x+15

  播放段落

  Step 3: Combine the x terms.
  ::第3步:将x项合并。

  播放段落

  $$\begin{align*}2x^2 - 6x - 5x + 15 = 2x^2 - 11x + 15\end{align*}$$
  ::2x2 - 6x - 5x+15=2x2 - 11x+15

  播放段落

  Answer :  $\begin{align*}2x^2 - 11x + 15\end{align*}$
  ::答复:2x2-11x+15

  播放段落

  To perform decomposition, these steps will need to be performed in reverse:
  ::为了进行分解,这些步骤需要逆向进行:

  播放段落
  1. Separate the x term into the sum of two terms that add to the original x term and multiply to the product of the  $\begin{align*}x^2\end{align*}$  term and the constant.
     ::将 x 术语分隔为两个词的总和,两个词加在原来的 x 术语上,乘在 x2 术语和常数的产物上。
  播放段落
  2. Take the greatest common factor out of the first two terms and last two terms.
     ::在前两个任期和最后两个任期中采用最大的共同因素。
  播放段落
  3. Take the greatest common factor out of the result of step 2.
     ::从第2步的结果中取出最大的共同因素。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Factor  $\begin{align*}2x^2 + 13x - 7\end{align*}$
  ::2x2+13x-7因数

  播放段落

  Step 1: Separate the x term into the sum of two terms that add up to the original x term but multiply to the product of the  $\begin{align*}x^2\end{align*}$  term and the constant.
  ::第1步:将x术语分为两个术语之和,两个术语加起来等于原来的x术语,但乘以 x2 术语和常数的产物。

  播放段落

  The product of the  $\begin{align*}x^2\end{align*}$  term and the constant is  $\begin{align*}2x^2 \cdot -7 = -14x^2.\end{align*}$   T he two terms that add up to  $\begin{align*}13x\end{align*}$  and multiply to  $\begin{align*}-14x^2\end{align*}$  will each have an  $\begin{align*}x\end{align*}$  so the focus will be placed on the coefficients. List the factors of -14 and look for the ones that add to 13.
  ::x2 术语和常数的产物为 2x2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  

  播放段落

  Since  $\begin{align*}-1 \cdot 14 = -14\end{align*}$   and  $\begin{align*}-1 + 14 = 13,\end{align*}$  the x term can be replaced with the sum of these factors: 
  ::由于-11414和--1+14=13,x字可以用这些因素的总和来取代:

  播放段落

  $$\begin{align*}2x^2 \textcolor{red}{+ 13x} -7 = 2x^2 \textcolor{red}{- 1x + 14x} - 7\end{align*}$$
  ::2x2+13x-7=2x2-1x+14x-7

  播放段落

  Step 2: Take the greatest common factor out of the first two terms and last two terms.
  ::第2步:在前两个任期和最后两个任期中采用最大的共同因素。

  播放段落

  The greatest common factor of the first two terms,  $\begin{align*}2x^2\end{align*}$  and  $\begin{align*}-1x,\end{align*}$   is  $\begin{align*}x.\end{align*}$  The greatest common factor of the last two terms is 7.
  ::前两个任期(2x2和-1x)的最大共同系数是x。 前两个任期的最大共同系数是7。

  播放段落

  $$\begin{align*}2x^2 - 1x + 14x - 7 = x(2x - 1) + 7(2x - 1)\end{align*}$$
  ::2x2 - 1x+14x-7=x(2x-1)+7(2x-1)

  播放段落

  A fter taking out the GCF, the value left in each set of the terms should be the same.  A  negative may need to be factored out to accomplish this.
  ::在提出全球合作框架之后,每一套术语所剩价值应当相同,为此可能需要计入负值。

  播放段落

  Step 3: Take the greatest common factor out of the result of step 2.
  ::第3步:从第2步的结果中取出最大的共同因素。

  播放段落

  Both  $\begin{align*}x(2x - 1)\end{align*}$  and  $\begin{align*}7(2x - 1)\end{align*}$  have a  $\begin{align*}(2x-1)\end{align*}$  as a common factor , so this will be factored out.
  ::x( 2x-1) 和 7( 2x-1) 都有一个共同系数( 2x-1) , 以作为共同系数, 因此, 这一点将被考虑在内 。

  播放段落

  $$\begin{align*}x(2x - 1) + 7(2x - 1) = (2x - 1)(x + 7)\end{align*}$$
  :x2x-1)+7(2x-1)=(2x-1)(x+7)

  播放段落

  Answer:  $\begin{align*}(2x - 1)(x + 7)\end{align*}$  
  ::答复2x-1)(x+7)

   

   

   

   

   

  播放段落

  Discussion Question :  Can you think  of  a shortcut for factoring quadratic expressions when $\begin{align*}a = 1?\end{align*}$   Does this work when $\begin{align*}a > 1?\end{align*}$
  ::讨论问题: 当 a=1 时, 您能想到计算二次表达式的快捷键吗? 当 a> 1 时, 这有用吗 ?

   

  ---

  播放段落

  Activity 4: Special Products
  ::活动4:特殊产品

  播放段落

  Some polynomials take on certain forms that make them easier to factor. While both the area model and decomposition will work for factoring these polynomials, knowledge of these shortcuts will come in handy as you progress throughout Algebra 2 . The first form  that  will  be discussed is known as the difference of squares .
  ::有些多面体有某些形式,使得它们更容易被考虑。虽然区域模型和分解都可用于计算这些多面体,但随着你在整个代数2中的进展,对这些捷径的了解将会有所帮助。 讨论的第一种形式被称为方形差异。

  播放段落

   Difference of Squares
  ::平方面积差异

  If a polynomial takes the form  $\begin{align*}a^2-b^2,\end{align*}$  it can be factored to  $\begin{align*}(a+b)(a-b).\end{align*}$  

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Factor  $\begin{align*}16x^2 - 81\end{align*}$
  ::16x2-81因数

  播放段落

  The term  $\begin{align*}16x^2\end{align*}$  is a perfect square where  $\begin{align*}\sqrt{16x^2} = 4x,\end{align*}$    $\begin{align*}81\end{align*}$  is a perfect square where  $\begin{align*}\sqrt{81} = 9,\end{align*}$  and the two numbers are being subtracted. The f orm above can be used to factor the binomial.
  ::16x2 是一个完美的正方形, 16x2=4x, 81是完美的正方形, 81=9, 并且正在减去这两个数字。 上面的表格可以用来计算二进制 。

  播放段落

  Answer :  $\begin{align*}16x^2 - 81 = (4x + 9)(4x - 9)\end{align*}$
  ::答复:16x2-81=(4x+9)(4x-9)

  播放段落

  When checking the answer by multiplying the factors together, it can be seen why this works.
  ::当通过乘以各种因素来检查答案时,人们可以看到为什么这个方法起作用。

  播放段落

  $$\begin{align*}(4x + 9)(4x - 9) &= 16x^2 + 36x - 36x - 81\\ &= 16x^2 - 81\end{align*}$$
  :4x+9)(4x-9)=16x2+36x-36x-81=16x2-81)

  播放段落

  Since the coefficients of the outer terms are the same as the coefficients of the inner terms except for the negative symbol, they will cancel when added. Canceling these terms leaves only the product of the first terms, which is a perfect square, and the product of the last terms, which is a perfect square.
  ::由于外用术语的系数与内用术语的系数相同,除负符号外,这些系数在增加时会取消。 取消这些术语只留下第一个术语的产物,第一个术语是完美的正方形,最后一个术语是完美的正方形。

  播放段落

    Perfect Square Trinomial
  ::完美广场三角广场

  If a polynomial takes the form  $\begin{align*}a^2 + 2ab + b^2,\end{align*}$  it can be factored to  $\begin{align*}(a+b)^2.\end{align*}$  

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Factor  $\begin{align*}9x^2 + 30x + 25\end{align*}$
  ::9x2+30x+25因数

  播放段落

  The term  $\begin{align*}9x^2\end{align*}$  is a perfect square where  $\begin{align*}\sqrt{9x^2} = 3x,\end{align*}$  the term  $\begin{align*}25\end{align*}$  is a perfect square where $\begin{align*}\sqrt{25} = 5, \end{align*}$  and  $\begin{align*}30x\end{align*}$  is double  $\begin{align*}3x \cdot 5.\end{align*}$   T he form above can be used to factor the trinomial.
  ::9x2 是一个完美的正方形, 其中 9x2=3x, 25 =5, 30x =2 3x5。 上面的表格可以用来计算三重。

  播放段落

  Answer :  $\begin{align*}9x^2 + 30 + 25 = (3x + 5)(3x + 5) = (3x + 5)^2\end{align*}$
  ::答复:9x2+30+25=(3x+5)(3x+5)=(3x+5)2

  播放段落

  When checking the answer by multiplying the factors together, it can be seen  why this works.
  ::当通过乘以各种因素来检查答案时,人们可以看到为什么这个方法起作用。

  播放段落

  $$\begin{align*}(3x + 5)(3x + 5) &= 9x^2 + 15x + 15x + 25 \\ &= 9x^2 + 30x + 25\end{align*}$$
  :3x+5)(3x+5)=9x2+15x+15x+25=9x2+30x+25)

  播放段落

  Since the coefficients of the outer terms are the same as the coefficients of the inner terms, they will double when added. Use the interactive below to further explore the concepts of the difference of squares and perfect square trinomials.
  ::由于外用术语的系数与内用术语的系数相同,如果加上的话,外用术语的系数将翻一番。 使用下面的互动来进一步探讨方形和完美的正方形三角差的概念。

   

   

   

   

   

   

  ---

  播放段落

  Extension: The Soccer Field Solution
  ::扩展名: 足球场解决方案

  播放段落

  Use the interactive below to explore .
  ::使用下面的互动来探索 。

   

   

   

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题

  

   

   

   

  播放段落

     Summary
  ::摘要

  播放段落
  • The process of factoring involves breaking up a number, term, polynomial, or expression into parts which, when multiplied, will produce the original expression.
    ::保理过程涉及将数字、术语、多义或表达式分成部分,如果乘以,将产生原始表达式。
  播放段落
  • A way to find the factors of a quadratic is to use decomposition, or reverse FOIL.
    ::找到二次方的因素的方法就是使用分解法或反向FOIL。
  播放段落
  • When a quadratic expression is written in the form  $\begin{align*}ax^2+bx+c,\end{align*}$  this is known as the standard form. When a quadratic expression is written as a product of its factors, this is known as the factored form.
    ::当四方形表达式以x2+bx+c的形式写成时,这被称为标准形式。当四方形表达式是其因子的产物而写成时,这被称为因子形式。
  播放段落
  • A polynomial that takes the form  $\begin{align*}a^2-b^2\end{align*}$  can be factored to  $\begin{align*}(a+b)(a-b).\end{align*}$  
    ::以 a2-b2 形式出现的多元性可乘以 (a+b (a-b) 。)
  播放段落
  • A polynomial that takes the form  $\begin{align*}a^2 + 2ab+b^2\end{align*}$  can be factored to  $\begin{align*}(a+b)^2.\end{align*}$  
    ::以 a2+2ab+b2 形式出现的多元值可乘以 (a+b) 2。