3.3 二次函数的特征-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节二次函数的特征

  折叠 展开

  二次函数的特征

  Lesson Objectives

  播放段落
  • Transform the graph of a quadratic function given the equation in vertex form.
    ::以顶点形式对等方程式的二次函数图形进行转换。
  播放段落
  • Find the vertex and axis of symmetry of a parabola given the equation in vertex form, standard form , and factored form .
    ::查找抛物线对称的顶点和轴, 以顶点形式、 标准形式 和因数形式 给出方程式 。
  播放段落
  • Identify  characteristics of a parabola : concave up or concave down, where it increases and decreases, and the domain and range , given the equation in vertex form, standard form, and factored form.
    ::确定抛物线的特性:向上或向下组合或组合,其增减和递减,以及域和范围,视等式为顶点形式、标准形式和因数形式。
  播放段落
  • Graph a parabola given the equation in vertex form, standard form, and factored form.
    ::以顶点形式、标准形式和系数形式给出方程式的参数图。
  播放段落
  • Compare the properties of two quadratics in the same and different forms.
    ::比较以相同和不同形式表现的两种象牙的特性。

  ---

  播放段落

  Introduction: Recreating Gravity
  ::导言:重力再生

  

  播放段落

  Quadratic functions are used to model many different scenarios  including  gravity. When an object is launched into the air or a person jumps, the path of their height behaves like an arc. This relationship is important to video game designers who want their games to have real-world physics. 
  ::二次曲线函数被用于模拟包括重力在内的许多不同情景。 当物体被射入空气或人跳跃时, 其高度的路径会像弧一样。 这种关系对于想要游戏具有真实世界物理学的视频游戏设计师来说很重要 。

   

   

   

  ---

  播放段落

  Activity 1: Vertex Form
  ::活动1:伏倒表

  播放段落

  The parent function  $\begin{align*}f(x) = x^2\end{align*}$  is the function on which all other quadratic functions are based. Every quadratic function is a transformation of the parent function. Using transformations ,  you can write the formula for any quadratic function. Use the interactive below to explore how transformations affect the vertex form of a quadratic. These transformations also impact the characteristics of the quadratic.
  ::父函数 f( x) =x2 是所有其他二次函数所基于的函数。 每个二次函数都是父函数的转换。 使用变换, 您可以为任何二次函数写入公式。 使用下面的交互功能来探索变换如何影响二次函数的顶部形式。 这些变换也会影响二次函数的特性 。

   

   

   

   

   

  播放段落

  Discussion Question : How does the axis of move in relation to the vertex. If the vertex is at (h, k) what would the equation for the axis of symmetry be?
  ::讨论问题:相对于顶点,移动轴如何。如果顶点在(h, k),对称轴的方程式是什么?

  ---

  播放段落

  Activity 2: Graphing in Vertex Form
  ::活动2:用Vertex格式绘制图表

  播放段落

  As the interactive above illustrates,  there is a relationship between the vertex form and the graph of the quadratic function.  You can use the characteristics of a  quadratic to graph a rough outline of the function and fill in any gaps with input-output pairs.
  ::如以上互动图所示,顶点形式与二次函数的图形之间存在某种关系。您可以使用二次函数的特性来绘制函数的粗略轮廓,并填补投入产出对等之间的任何空白。

  播放段落

  Given a function in vertex form, you can find all of the following before even graphing the function:
  ::给定顶点形式的函数,您可以在图形化函数之前找到所有以下函数:

  播放段落
  • vertex
    ::顶向
  播放段落
  • axis of symmetry
    ::对称轴
  播放段落
  • $\begin{align*}y\text{-}\end{align*}$ intercept
    ::y 界面
  播放段落
  • $\begin{align*}x\text{-}\end{align*}$ intercepts
    ::x 界面
  播放段落
  • intervals of increase/decrease
    ::增加/减少的间隔期
  播放段落
  • domain
    ::域域域域域域
  播放段落
  • range
    ::范围范围
  播放段落
  • concavity
    ::混凝度

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Jason is a product manager for a home security company. Through focus groups and testing he has modeled the following function to represent the profit, in thousands, as a function of the price for a new home security camera:  $\begin{align*}f(x) = -(x - 32)^2 + 529.\end{align*}$   Given this function, state the following and what they mean to the context of the problem.
  ::Jason是一家家用保安公司的产品经理,通过重点小组和测试,他模拟了以下功能,以代表收益,以千计,作为新家用保安摄像头价格的函数:f(x)(x-32)2+529。

  播放段落
  1. Concavity
     ::混凝度
  播放段落
  2. The vertex
     ::顶点
  播放段落
  3. The equation for the axis of symmetry
     ::对称轴的方程
  播放段落
  4. Any intervals of increase or decrease
     ::任何增减间隔
  播放段落
  5. The $\begin{align*}y-\end{align*}$ intercept
     ::y- interacut y- interinter y- intercide y- intercide y- intercide y- intercinter y- intercide y- intercide y- intercide y- intercide y- intercide y- intercide y- inter y- inter y- intercide y- intercide y- inter y- inter inter y- inter inter y- inter inter inter y- inter inter inter y- inter inter inter inter y- inter inter inter inter inter y- inter- inter 界面
  播放段落
  6. Domain and Range
     ::域和范围

  播放段落

  a. Concavity
  ::a. 混凝土

  播放段落

  As  you saw in the previous interactive, if $\begin{align*}a\end{align*}$   is positive, the parabola will be concave up. If $\begin{align*}a\end{align*}$   is negative, the parabola will be concave down. Since $\begin{align*}a\end{align*}$   is -1, the parabola formed by the function  $\begin{align*}f(x) = -1(x - 32)^2 + 529\end{align*}$   will be concave down. Concave down means that the ends of the parabola will point down. In the context of the problem, this means that the profit will rise and fall as the price increases. At first, raising the price will increase the profit, but once the price gets too high, the profit will decrease.
  ::正如您在上一个互动中看到的那样, 如果是正的话, 抛物线会变大。 如果是负的, 抛物线会变小。 因为 : - 1, 函数 f( x) 1 (x- 32) 2+529 所形成的抛物线会变小。 缩小意味着抛物线的终点会下降。 在问题的背景下, 这意味着利润会随着价格的上涨而上升和下降。 首先, 提高价格会增加利润, 但一旦价格太高, 利润就会下降 。

  播放段落

  b. The vertex
  ::b. 顶点

  播放段落

  You  also saw in the interactive above that the vertex of a quadratic function in vertex form will be at  $\begin{align*}(h,k).\end{align*}$  In the function  $\begin{align*}f(x) = -(x - 32)^2 + 529,\end{align*}$   $\begin{align*}h\end{align*}$   is 32, and $\begin{align*}k\end{align*}$  is 529. Thus, the vertex will be at $\begin{align*}(32, 529).\end{align*}$  Additionally, since the parabola is concave down,  you know that the vertex is the maximum value. The maximum profit of $529,000 will occur when the price of the security camera is set to $32.
  ::在上文的互动中,你还看到,顶点形式的二次函数的顶点将位于(h,k)。在 f(x)(x-32(x-32)2+529,h为32,k为529。因此,顶点将位于(32,529),此外,由于抛物线正在下沉,你知道顶点是最大值。当安全相机的价格定在32美元时,最高利润529,000美元将出现。

  播放段落

  c. The equation for the axis of symmetry
  ::c. 对称轴方程式

  播放段落

  The axis of symmetry will always run through the vertex, sharing the same $\begin{align*}x-\end{align*}$ coordinate. Therefore , the equation of the axis of symmetry will always be  $\begin{align*}x = h.\end{align*}$   In this case, the equation of the axis of symmetry will be  $\begin{align*}x = 32.\end{align*}$  In the context of the scenario, the profit is symmetrical about the price of $32.  The home security company will make as much profit by setting the price to $30 as  the company  would by setting the price to $34.
  ::对称轴将总是穿过顶端, 并共用相同的x- 坐标。 因此, 对称轴的方程式将始终是x=h。 在这种情况下, 对称轴的方程式将是x=32。 在这种假设情况下, 利润对称于32美元的价格。 母国保安公司通过将价格定在30美元, 将价格定在34美元, 从而获得同样多的利润。

  播放段落

  d. Identify any intervals of increase or decrease
  ::d. 确定任何增减间隔

  播放段落

  Given that the parabola is concave down,  you know that it will increase from left to right until it reaches the vertex and will decrease afterward. Thus it will increase from the $\begin{align*}x-\end{align*}$  values of  $\begin{align*}(-∞,32)\end{align*}$   and decrease from the $\begin{align*}x-\end{align*}$  values of  $\begin{align*}(32,∞).\end{align*}$   Do not include 32 in either interval because the graph is neither increasing nor decreasing at the vertex. As the price increases toward $32, the profit is increasing. As the price continues to increase beyond $32, the profit will decrease.
  ::鉴于抛物线正在向下变形, 您知道它会从左向右上升, 直到到达顶端, 然后会下降。 因此它会从x- 值( , 32) 和x- 值( 32, ) 中增加, 并且从x- 值( 32, ) 中减少。 因为图形在顶端既不增加, 也不会减少, 间隔中不包括32 。 随着价格上升到32 美元, 利润也在增加 。 随着价格继续上升超过 32 美元, 利润将会下降 。

  播放段落

  e . State the $\begin{align*}y-\end{align*}$ intercept
  ::e. 说明y- 互动情况

  播放段落

       To find the $\begin{align*}y-\end{align*}$ intercept of a function, first locate the output at  $\begin{align*}f(0).\end{align*}$
  ::要找到函数的 y- 界面, 请首先将输出定位在 f( 0) 上 。

  播放段落

  $$\begin{align*}f(0) &= -(0 - 32)^2 + 529\\ &= -(-32)^2 + 529\\ &= -(1,024) + 529\\ &= -1,024 + 529\\ &= -495\end{align*}$$
  ::f( 0) ( 0) ( 32) 2+529 ( 32) 2+529 (1 024)+529 1 024+529 1 024+529+529 1 024+529+529

  播放段落

  The $\begin{align*}y\end{align*}$  -intercept is  $\begin{align*}(0,-495).\end{align*}$  In this context, this means that giving security cameras away for free will result in a profit of $-495,000. It makes sense that this would lead to debt considering the money it would cost to make the cameras that were given away for free.
  ::y - 拦截是( 0,-495 ) 。 在这一点上,这意味着免费提供监控摄像头将带来495,000美元的利润。 考虑到免费拍摄摄像头的成本,这将导致债务。

  播放段落

  f. Domain and Range
  ::f. 域和范围

  播放段落

  The domain of the function  $\begin{align*}f(x) = -(x - 32)^2 + 529\end{align*}$  is all real numbers since any real number can be substituted in for $\begin{align*}x.\end{align*}$   However, in the context of the problem, the domain may vary. A domain that covers any price greater than or equal to 0 may be more appropriate. Therefore  the domain, in this context, would be  $\begin{align*}[0, ∞)\end{align*}$  which can also be written as  $\begin{align*}x ≥ 0.\end{align*}$   The security company  may also want to consider a domain that will only produce a positive profit. This domain would be in an interval defined by the $\begin{align*}x\end{align*}$  -intercepts, which is the focus of the lesson Roots of Quadratic Functions . The range of the function is  $\begin{align*}y≤529\end{align*}$  since the maximum output value is 529. In the context of the problem, this means that  the company cannot make more money than the maximum profit. Keep in mind, setting restrictions on the domain might affect the range. For example, setting the domain to only values that will produce a positive profit will restrict the range to that domain resulting in a range that can only be positive.
  ::函数 f( x) {( x- 322) 2+529 的域可能是真实数字, 因为任何真实数字都可以替换为 x 。 但是, 在问题的背景下, 域可能有所不同。 覆盖任何价格大于或等于 0 的域可能更为合适 。 因此, 在这方面, 域将是 [ , 也可以写成 x+0 。 安全公司还可能想要考虑一个仅产生正利润的域 。 域将位于x - interfits 所定义的间隔内, 这是 Quadratic 函数的课根的焦点 。 函数的范围是 y 529, 因为最大输出值为 529 。 在问题的背景下, 这意味着公司不能赚更多的钱来达到最大利润 。 记住, 对域设限制可能会影响范围 。 例如, 将域设为只产生正利润的值, 将会限制域的范围, 导致范围只能是肯定的域 。

  播放段落

  The graph of  $\begin{align*}f(x) = -(x - 32)^2 + 529\end{align*}$  would appear as follows:
  ::f(x)(x-32)2+529的图表如下:

  

   

   

   

  ---

  播放段落

  Activity 3: Standard Form
  ::活动3:标准表格

  播放段落

  M ultiplying out a quadratic function in vertex form,  results in what is known as the standard form. The standard form of a quadratic function is  $\begin{align*}f(x) = ax^2 + bx + c\end{align*}$   where $\begin{align*}a\end{align*}$   is the coefficient of the $\begin{align*}x^2\end{align*}$   term , $\begin{align*}b\end{align*}$   is the coefficient of the $\begin{align*}x\end{align*}$   term, and $\begin{align*}c\end{align*}$   is the constant . Although the characteristics for this form are slightly less intuitive than when in vertex form, this form is commonly used. U se the same strategy of identifying characteristics and plotting input-output pairs to graph a quadratic equation in standard form.
  ::以顶点形式乘出二次函数, 以标准形式产生。 二次函数的标准形式是 f( x) = ax2+bx+c, 其中一种函数是 x2 术语的系数, b 是 x 术语的系数, c 是恒定的。 虽然这种形式的特性比顶点形式时略微不直观, 但通常使用这种形式。 使用相同的战略来识别特性和绘制输入输出对方以标准形式绘制二次方程 。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  A firework is launched from a platform 29 feet off the ground with an initial velocity of 112 ft/s. The height of the firework can be modeled as a function of time using the function  $\begin{align*}f(x) = -16x^2 + 112x + 29.\end{align*}$   Given this function, state the following and what they mean to the context of the problem.
  ::从离地29英尺的平台上发射烟花,最初速度为112英尺/秒。烟花的高度可以用函数 f(x)\\\\16x2+112x+29作为时间函数模型。鉴于此功能,请说明以下内容及其对问题背景的意义。

  播放段落

  a. Concavity
  ::a. 混凝土

  播放段落

  Much like with vertex form,  you can determine the concavity based on the value of $\begin{align*}a,\end{align*}$   the coefficient of the  $\begin{align*}x^2\end{align*}$   term. If $\begin{align*}a\end{align*}$   is positive, the parabola will be concave up. If $\begin{align*}a\end{align*}$   is negative, the parabola will be concave down. Since $\begin{align*}a\end{align*}$   is -16, which is less than 0, this parabola will be concave down. The height of the object will increase until it reaches its maximum at which point the height will decrease.
  ::与顶点形式相似, 您可以根据一个值确定混凝土, 即 x2 术语的系数。 如果是正值, 抛物线会向上凝聚。 如果是负值, 抛物线会向下凝聚。 由于是 - 16, 它小于 0, 此抛物线会向下凝聚。 对象的高度会升高, 直到它达到最大高度的点 。

  播放段落

  b. The vertex
  ::b. 顶点

  播放段落

  In standard form, the vertex is not immediately obvious. The $\begin{align*}x-\end{align*}$ coordinate of the vertex can be found using the formula  $\begin{align*}x = \frac{-b}{2a}.\end{align*}$
  ::在标准格式中, 顶点并不立即明显。 顶点的 x - 坐标 可以用公式 x b2a 找到 。

  播放段落

  $$\begin{align*}x &= \frac{-112}{2(-16)}\\ \\ &= \frac{-112}{-32} \\\\ &= 3.5\end{align*}$$
  ::x11122(- 16) 112-32=3.5

  播放段落

  Once  you have the $\begin{align*}x-\end{align*}$ coordinate, substitute it into the function to obtain the $\begin{align*}y-\end{align*}$  coordinate.
  ::一旦您有了x- 坐标, 将它替换为函数, 以获得 y- 坐标 。

  播放段落

  $$\begin{align*}y = f(3.5) &= -16(3.5)^2 + 112(3.5) + 29\\ &= -16(12.25) + 112(3.5) + 29\\ &= -196 + 392 + 29 \\&= 225\end{align*}$$
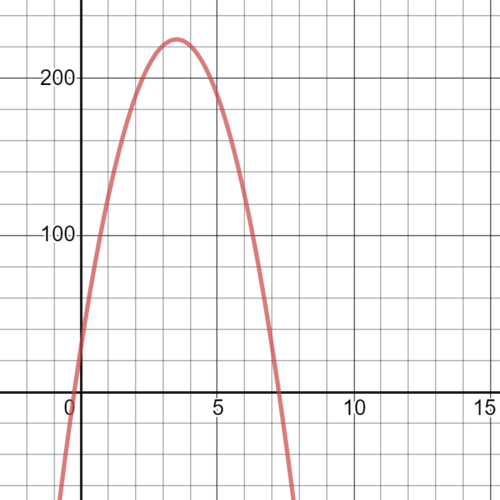
  ::y=f(3.5) =16(3.5) 16(3.5)2+112(3.5)+29(3.5)+16(12.25)+112(3.5)+29*196+392+29=225

  播放段落

  The vertex of the function is  $\begin{align*}f(x) = -16x^2 + 112x + 29\end{align*}$   is  $\begin{align*}(3.5, 225).\end{align*}$   The object will reach its maximum height of 225 feet, 3.5 seconds after being launched.  This formula is  explored further in  the lesson   .
  ::函数的顶点是 f(x)\\\ 16x2+112xx+29 是 (3.5, 225) 。 对象最大高度将达到 225 英尺, 发射后3.5 秒。 此公式将在课程中进一步探讨 。

  播放段落

  c. The equation for the axis of symmetry
  ::c. 对称轴方程式

  播放段落

  As in vertex form, the axis of symmetry  is always equal to the $\begin{align*}x-\end{align*}$ coordinate of the vertex. Therefore, the equation of the axis of symmetry is  $\begin{align*}x = 3.5.\end{align*}$   The height of the object is symmetrical about this line .
  ::与顶点形式一样,对称轴始终等于顶点的 x - 坐标。因此,对称轴的方程式是 x= 3.5。对象的高度与该直线的高度对称。

  播放段落

  d. Any intervals of increase or decrease
  ::d. 任何增减间隔

  播放段落

  Since the parabola is concave down, it will increase until it reaches the vertex at 3.5 seconds and then decrease. Thus, it will increase from the $\begin{align*}x-\end{align*}$ values of  $\begin{align*}(-∞,3.5)\end{align*}$   and decrease from the $\begin{align*}x-\end{align*}$ values of  $\begin{align*}(3.5,∞).\end{align*}$
  ::由于抛物线向下沉,它会增加,直到在3.5秒到达顶部,然后下降。因此,它会从X-值(,3.5)到X-值(3.5,)而减少。

  播放段落

  e. The $\begin{align*}y-\end{align*}$ intercept
  ::e. y- 界面

  播放段落

  To find the $\begin{align*}y-\end{align*}$ intercept of a function, locate the output at  $\begin{align*}f(0).\end{align*}$
  ::要找到函数的 y- 界面, 请将输出定位为 f( 0) 。

  播放段落

  $$\begin{align*}f(0) &= -16(0)^2 + 112(0) + 29\\ &= -16(0) + 112(0) + 29\\ &= 29\end{align*}$$
  ::f( 0) 16( 0) 16( 0) 2+112( 0)+112( 0)+29} 16( 0)+112( 0)+112( 0)+29=29

  播放段落

  Notice that the $\begin{align*}y-\end{align*}$ intercept is the constant in the function. Substituting 0 into the function will eliminate any terms with variables leaving only the constant. In many contexts, including this one, the $\begin{align*}y-\end{align*}$ intercept represents the starting $\begin{align*}y-\end{align*}$ value of the function. The platform is 29 feet above the ground, which is the starting height of the object.
  ::注意 y - 界面是函数中的常数。 在函数中将 0 替换为 0 将删除任何条件, 变量只留下常数。 在很多情况下, 包括此情况下, y - 界面代表函数的起始 y - 值 。 平台位于地面上29 英尺, 即天体的起始高度 。

  播放段落

  f. Domain and Range
  ::f. 域和范围

  播放段落

  The domain of all quadratic functions is all real numbers because  you can substitute any real number in for $\begin{align*}x.\end{align*}$   However, in the context of the problem, the domain would start at 0 seconds and end when the object lands since the relationship between height and time is not true outside of these times. The object hits the ground at 7.25 seconds; thus, the domain will be  $\begin{align*}[0, 7.25].\end{align*}$   The lesson Roots of Quadratic Functions  discusses how to obtain this piece of information. The range of the function  $\begin{align*}f(x) = -16x^2 + 112x + 29\end{align*}$   is  $\begin{align*}(-∞, 225].\end{align*}$   T he vertex, $\begin{align*}(3.5, 225),\end{align*}$  indicates that $\begin{align*}225\end{align*}$  is the maximum value. In this context, a range of  $\begin{align*}[0, 225]\end{align*}$  is appropriate, covering the maximum height to the when the rocket hits the ground. This range also works with the domain of the function.
  ::所有二次函数的域都是真实数字, 因为您可以在 x 中替换任何真实数字。 但是, 在问题的背景下, 域将开始于 0 秒, 当天体着陆时结束, 因为高度和时间之间的关系在这些时间之外是不真实的。 对象撞击地面的时间是7. 25 秒; 因此, 域将是 [ 0. 25 秒 。 二次函数的课根将讨论如何获取此信息 。 函数 f( x) 16x2+112x+29 的范围是 (, 225) 。 顶点 (3.5, 225) 表示 225 是最大值 。 在此情况下, [ 0225 范围是合适的, 覆盖火箭撞击地面时的最大高度 。 此范围也与函数的域有关 。

  播放段落

  The graph of  $\begin{align*}f(x) = -16x^2 + 112x + 29\end{align*}$   would appear as follows:
  ::f(x)16x2+112x+29的图表如下:

  

   

   

   

  ---

  播放段落

  Activity 4: Factored Form
  ::活动4:有因素的形式

  播放段落

  The lesson Graphing Quadratic Functions explores  how to factor a quadratic expression . U se these techniques to write a quadratic function in factored form. The factored form of a quadratic function is  $\begin{align*}f(x) = a(x - p)(x - q).\end{align*}$   The coefficient $\begin{align*}a,\end{align*}$  causes the quadratic to scale in the same way that it does in vertex form and standard form. The variables $\begin{align*}p\end{align*}$   and $\begin{align*}q\end{align*}$   represent the $\begin{align*}x\end{align*}$ -intercepts of the quadratic function.
  ::课程刻度函数绘图 探索如何乘以二次表达式 。 使用这些技术来以分系数形式写入二次函数 。 二次函数的系数形式是 f( x) =a( x- p)( x- q) 。 系数a , 导致二次函数以与顶点形式和标准形式相同的方式缩放。 变量 p 和 q 代表二次函数的 x 界面 。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  The height as a function of distance traveled from a character’s position along the $\begin{align*}x-\end{align*}$ axis can be modeled by the function $\begin{align*}f(x)= -0.05(x+1)(x-39).\end{align*}$  Distances in most video games are in relative units; in this case, the relative units  is called meters. Given this function, state the following characteristics and what they mean to the context of the problem.
  ::函数 f( x) = = = = = = = = 1 ( x- 39) 可以模拟从字符在 x - 轴位置上移动的距离的高度函数。 大多数电子游戏的距离是相对单位; 在这种情况下, 相对单位被称为米。 根据此函数, 说明以下特性及其对问题背景的意义 。

  播放段落

  a. Concavity
  ::a. 混凝土

  播放段落

  Since the $\begin{align*}a\end{align*}$   coefficient in the game is $\begin{align*}-0.05,\end{align*}$   the parabola  is concave down. The character will rise through the air and then fall.
  ::由于游戏中的系数是- 0.0 5, 抛物线会下降。 字符会从空气中上升, 然后下降 。

  播放段落

  b. The vertex
  ::b. 顶点

  播放段落

  The $\begin{align*}x-\end{align*}$ coordinate of the vertex of a parabola will always be in the middle of the $\begin{align*}x-\end{align*}$ intercepts. To find the middle of two values, add them and divide by 2 . T he $\begin{align*}x-\end{align*}$ intercepts are given as $\begin{align*}-1\end{align*}$   and $\begin{align*}39.\end{align*}$    So, the $\begin{align*}x-\end{align*}$ coordinate of the vertex can be found by dividing the sum by 2 :
  ::抛物线顶端的x- 坐标将始终处于 x- 截面中间。 要找到两个值的中间点, 添加它们, 并除以 2 。 x- 截面被标为-1 和 39 。 因此, 通过将总和除以 2 , 可以找到顶端的 x- 坐标 :

  $$\begin{align*}\frac{-1 + 39}{2} = 19\end{align*}$$

  播放段落

  To find the $\begin{align*}y-\end{align*}$ coordinate of the vertex, substitute the $\begin{align*}x-\end{align*}$ coordinate of the vertex into the function.
  ::要找到顶点的 Y - 坐标, 请在函数中替换顶点的 x - 坐标 。

  播放段落

  $$\begin{align*}f(19) &= -0.05((19)+1)((19)-39) \\ &= -0.05(20)(-20) \\ &= -0.05(-400) \\ &= 20\end{align*}$$
  :19) 0.05(19)+1(19)-39) 0.005(20) (20) 0.005(-400)=20

  播放段落

  The vertex of the equation is  $\begin{align*}(19,20),\end{align*}$  which means that when the character has traveled 19 meters, it will reach its maximum height of 20 meters.
  ::方程的顶点是19,20, 这意味着当字符飞行了19米时, 它会达到20米的最高高度。

  播放段落

  c. The equation for the axis of symmetry
  ::c. 对称轴方程式

  播放段落

  The axis of symmetry is  $\begin{align*}x = 19\end{align*}$   because the axis of symmetry runs vertically through the $\begin{align*}x-\end{align*}$ coordinate of the vertex.
  ::对称轴为x=19,因为对称轴垂直穿过顶端的 x- 坐标。

  播放段落

  d. Identify any intervals of increase or decrease
  ::d. 确定任何增减间隔

  播放段落

  Since the parabola is concave down, the character will increase over the interval  $\begin{align*}(-∞,19)\end{align*}$  and decrease over the interval  $\begin{align*}(19,∞).\end{align*}$  The character’s height will increase until it has traveled 19 feet along the $\begin{align*}x-\end{align*}$ axis, at which point the height will decrease.
  ::由于抛物线正在下沉,字符会随着间隔增加(,19)和间隔减少(19,19)。 字符的高度会增加,直到它沿着 x - 轴飞行19英尺,到时高度会下降。

  播放段落

  e. State the $\begin{align*}y-\end{align*}$ intercept
  ::e. 说明y- 互动情况

  播放段落

  To find the $\begin{align*}y-\end{align*}$ intercept of a function, locate the output at  $\begin{align*}f(0).\end{align*}$
  ::要找到函数的 y- 界面, 请将输出定位为 f( 0) 。

  播放段落

  $$\begin{align*}f(0) &= -0.05((0) + 1)((0) - 39) \\ &= -0.05(1)(-39) \\ &= -0.05(-39) \\ &= 1.95\end{align*}$$
  ::f(0) 0.05(0)+1(0)-(39) 0.05(1)-(39) 0.005(39) =1.95

  播放段落

  The $\begin{align*}y-\end{align*}$ intercept is  $\begin{align*}(0,1.95),\end{align*}$  which is the starting position of the character.
  ::y- 界面是 (0, 1.95) , 这是字符的起始位置 。

  播放段落

  f. Domain and Range
  ::f. 域和范围

  播放段落

  The domain of the function  $\begin{align*}f(x)= -0.05(x+1)(x-39)\end{align*}$  is again all real numbers since any real number can be substituted  for $\begin{align*}x.\end{align*}$  In the context of the problem, the domain begins when the character is launched at 0 meters and ends when the character hits the ground at 39 meters. A domain of  $\begin{align*}[0,39]\end{align*}$   would be appropriate. The lowest height of the character is 0 meters, and the maximum height of the character is 20 meters; thus, the range should be  $\begin{align*}[0,20].\end{align*}$
  ::函数 f(x)\\ 0.05(x+1)(x- 39) 的域再次成为所有真实数字,因为任何实际数字都可以替换 x。 在问题的背景下, 域始于字符在0米处启动时, 结束于字符在39米处撞击地面时。 [ 0. 39] 的域是合适的。 字符的最小高度为 0米, 字符的最大高度为 20米; 因此, 范围应该是 [ 020] 。

  播放段落

  The graph of  $\begin{align*}f(x)= -0.05(x+1)(x-39)\end{align*}$   would appear as follows:
  ::f(x)0.05(x+1)(x-39)的图表如下:

  

  播放段落

  Explore a quadratic in  factored form as it applies to bridge construction in the  interactive below.
  ::在下文互动部分探讨适用于桥梁建造的因数式二次曲线。

   

   

   

  ---

  播放段落

  Activity 5: Putting it All Together
  ::活动5:团结共事

  播放段落

  Now that you are familiar with the forms of a quadratic function. Use the interactive below to practice graphing quadratic functions in any form.
  ::现在您已经熟悉了二次函数的形式。 使用下面的互动来练习以任何形式绘制二次函数的图形 。

   

   

   

   

   

  ---

  播放段落

  Extension: Quadratic Functions and Equations
  ::扩展: 二次函数和等量

  播放段落

  Use the interactive below for more practice relating to their equations.
  ::使用下面的交互式文字,以了解与其方程式有关的更多实践。

   

   

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题

  

   

   

   

  ---

  播放段落

  Extension: Characteristics of Quadratic Functions Practice
  ::扩展: 二次函数惯例的特点

  播放段落

  Use the interactive below to practice identifying and interpreting the characteristics of quadratic functions.
  ::利用下面的交互作用,确定和解释二次函数的特性。

   

   

   

  播放段落

     Summary
  ::摘要

  播放段落

  The vertex form of a quadratic is  $\begin{align*}y=a{(x-h)}^{2}+k\end{align*}$
  ::二次方形的顶部形为 y=a(x-h)2+k

  播放段落
  • The vertex is  $\begin{align*}(h,k)\end{align*}$  
    ::顶点是 (h, k)
  播放段落
  • The axis of symmetry is  $\begin{align*}x=h\end{align*}$  
    ::对称轴为 x=h
  播放段落
  • If $\begin{align*}a\end{align*}$   is positive, the parabola  is concave up
    ::如果呈阳性, 抛物线就会凝聚起来
  播放段落
  • If $\begin{align*}a\end{align*}$   is negative, the parabola is concave down
    ::如果一个是负的, 抛物线正在下沉

  播放段落

  The standard form of a quadratic is  $\begin{align*}f(x)=a{x}^{2}+bx+c\end{align*}$
  ::二次方的标准形式是 f( x) = ax2+bx+c

  播放段落
  • Use the formula  $\begin{align*}x=\tfrac{-b}{2a}\end{align*}$  to find the $\begin{align*}x\text{-}\end{align*}$ coordinate of the vertex and the axis of symmetry
    ::使用公式 xb2a 查找顶点和对称轴的x坐标
  播放段落
  • If $\begin{align*}a\end{align*}$   is positive, the parabola is concave up
    ::如果呈阳性, 抛物线就会凝聚起来
  播放段落
  • If $\begin{align*}a\end{align*}$   is negative, the parabola is concave down
    ::如果一个是负的, 抛物线正在下沉

  播放段落

  The factored form of a quadratic is  $\begin{align*}f(x)=a(x-p)(x-q)\end{align*}$
  ::梯度的系数形式为 f(x)=a(x-p)(x-q)

  播放段落
  • Find the $\begin{align*}x\text{-}\end{align*}$ coordinate of the vertex by finding the point in between the two $\begin{align*}x\text{-}\end{align*}$ intercepts
    ::通过在两个 X 界面之间找到点来查找顶点的 x 坐标
  播放段落
  • Use the formula  $\begin{align*}x=\tfrac{-q-p}{2}\end{align*}$  to find the $\begin{align*}x\text{-}\end{align*}$ coordinate of the vertex and the axis of symmetry
    ::使用公式 xq- p2 查找顶点和对称轴的 x坐标
  播放段落
  • If $\begin{align*}a\end{align*}$   is positive, the parabola  is concave up
    ::如果呈阳性, 抛物线就会凝聚起来
  播放段落
  • If $\begin{align*}a\end{align*}$   is negativ,e the parabola is concave down
    ::如果一个是纳加提夫,e 抛物线正在向下凝结