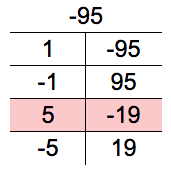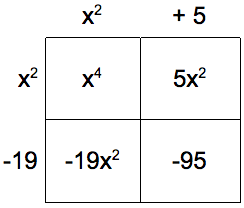4.1 使用量衡法对聚合物进行乘数计算-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 使用二次曲线法计算聚合系数

  Collapse Expand

  使用二次曲线法计算聚合系数

  Lesson Objectives

  播放段落
  • Factor with degree greater than two by finding the greatest common factor .
    ::通过找到最大的共同因素,因子大于2,因子大于2。
  播放段落
  • Factor polynomials with degree greater than two using difference of squares .
    ::使用方形差异的系数多元度大于2倍的系数。
  播放段落
  • Factor polynomials with degree greater than two by grouping.  
    ::按组别计算,系数的多元度大于2。

  ---

  播放段落

  Introduction:  Connecting Polynomials to Numbers
  ::导言:将多面体连接到数字

  播放段落

  There are c onnections between polynomials and integers that you've probably explored previously to  understand polynomial operations .  You can also take advantage of this connection to help understand factoring.
  ::多数值和整数之间有些关联, 您可能已经探索过这些关联来理解多数值操作。 您也可以利用这些关联来帮助理解乘数 。

  播放段落

  Use the interactive below to explore this connection with quadratic expressions.
  ::使用下面的交互方式来探索二次表达式的这种关联。

  播放段落

  A prime polynomial , also known as an irreducible polynomial , is a polynomial that cannot be written as a product of factors with a lower degree.  The goal in this section will not only be determining if a polynomial is prime but to  find the prime factorization. The prime factorization of a polynomial is when the polynomial is written as a product of its prime factors. In this section, you will practice with a degree greater than 3. 
  ::一个称为不可减少的多元性的主要多元性,是一个不能作为较低程度因素的产物来写成的多元性,本节的目标不仅在于确定一个多元性是否为首要因素,而且在于找到主要因素。一个多元性的主要因素是当多元性被写成是其主要因素的产物时。在本节中,你将练习超过3个的等级。

   

  ---

  播放段落

  Activity 1: Greatest Common Factor
  ::活动1:最大共同因素

  播放段落

  In the example below, dividing the greatest common factor  from an expression will be extended to help factor a cubic polynomial. A cubic polynomial is a degree 3 polynomial that can be written in the standard form  $\begin{align*}ax^3 + bx^2 + cx + d.\end{align*}$   On the surface, this example of a third-degree trinomial may look difficult to factor, but it can be factored  using techniques that learned in Factoring Quadratic Functions and Rational and Irrational Roots. Much like when factoring a quadratic, t he first thing to look for when factoring a polynomial is the greatest common factor.
  ::在下面的例子中,将最大共同系数从表达式中除以最大共同系数将扩大,帮助乘以立方体多元值。立方多数值是第3级多数值,可以用标准方形x3+bx2+cx+d写成。在表面,第三度三角值的这个例子可能很难计算出来,但可以用在计算二次函数函数函数函数函数函数函数函数函数函数函数函数函数函数函数法和理性和不光学根法中学习的技术来计算。非常像在计算二次系数时,当计算一个多边系数时,首先需要寻找的就是最大的共同系数。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  The concentration, in parts per million, of a medicine in a patient’s bloodstream after x hours can be modeled using the polynomial  $\begin{align*}0.002x^3 - 0.16x^2 + 3.2x,\end{align*}$   given a specific domain that will be  discussed   shortly . Write this polynomial as a product of its prime factors.
  ::病人在x小时后的血液中的药物浓度,在百万分之一,可以使用多元体 0.002x3-0.16x2+3.2xx来模拟。 具体领域不久将讨论。 将这一多元体写成其主要因素的产物。

  播放段落

  To begin, look for the greatest common factor. Each term has a factor of x, so begin by  dividing  an x from each term.
  ::首先,寻找最大的共同因素。每个术语有一个 x 系数, 所以首先从每个术语中除以 x 开始 。

  播放段落

  $$\begin{align*}0.002x^3 - 0.16x^2 + 3.2x = x \cdot (0.002x^2 + 0.16x + 3.2)\end{align*}$$
  ::0002x3-0.16x2+3.2x=x(0.002x2+0.16x+3.2)

  播放段落

  Since it is difficult to make sense of these numbers, a  decimal factor can be removed to make the coefficients whole numbers. M ove the decimal three places to the right to cancel the decimals. To do this, divide out a  $\begin{align*}\tfrac{1}{1,000}.\end{align*}$   Dividing by $\begin{align*}\tfrac{1}{1,000},\end{align*}$   or .001, will have the same effect as multiplying by 1,000 since division involves multiplying by the reciprocal .
  ::由于难以理解这些数字,因此可以删除一个小数点系数,使系数成为全部数字。将小数点的三位移到取消小数点的权利上。要做到这一点,将11 000除以1 000。除以11 000,或.001,将具有与乘以1 000相同的效果,因为除法涉及乘以对等法。

  播放段落

  $$\begin{align*}x \cdot (0.002x^2 - 0.16x + 3.2) = 0.001 \cdot x \cdot (2x^2 - 160x + 320)\end{align*}$$
  ::x( 0.002x2 - 0. 16x+3.2) = 0.001x}( 2x2 - 160x+320)

  播放段落

  Now that the coefficients are whole numbers, it is easier to see that a factor of 2 can be removed from each term.
  ::由于系数是整数,因此更容易看出从每个术语中可以删除2系数。

  播放段落

  $$\begin{align*}0.001 \cdot x \cdot (2x^2 + 160x + 320) &= 2 \cdot 0.001 \cdot x \cdot (x^2 + 80x + 160) \\ &= 0.002x(x^2 + 80x + 1600)\end{align*}$$
  ::x( 2x2+160x+320) = 20.001x}( x2+80x+160) = 0.002x( x2+80x+1600)

  播放段落

  After dividing  out a GCF ,  attempt to factor the trinomial $\begin{align*}x^2 + 80x + 1600.\end{align*}$    Since the  $\begin{align*}x^2\end{align*}$   coefficient is 1, find factors of the constant that add up to the x coefficient.  You should also be able to see that this is a perfect square trinomial . The square root of 1600 is 40 and  $\begin{align*}40 + 40 = 80.\end{align*}$
  ::将绿色气候基金分离出来后, 尝试乘以三元x2+80x+1600。 由于 x2 系数为 1, 找到与 x 系数相加的常数系数。 您也应该能看到这是一个完美的平方三角。 1600 的平方根为 40 和 40+40=80 。

  播放段落

  $$\begin{align*}0.002x(x^2 + 80x + 1600) = 0.002x(x + 40)(x + 40)\end{align*}$$
  ::002x(x2+80x+1600=0.002x(x+40)(x+40)

  播放段落

  Answer:   $\begin{align*}0.002x(x + 40)(x + 40)\end{align*}$
  ::答复:0.0002x(x+40)(x+40)

  播放段落

  In retrospect, you could have immediately factored out the 0.002 to produce integer coefficients. However, the simplest strategy may not always be immediately evident. This answer represents the prime factorization of  $\begin{align*}0.002x^3 - 0.16x^2 + 3.2x.\end{align*}$   Any product that is a combination of the prime factors will be  a factor to  $\begin{align*}0.002x^3 - 0.16x^2 + 3.2x.\end{align*}$
  ::回过头来看,你本可以立即将0.002乘以生成整数系数。然而,最简单的策略不一定总能立即显现出来。这个答案代表了0.002x3-0.16x2+3.2x。任何产品,如果是主要因素的组合,均是0.002x3-0.16x2+3.2x的一个系数。

   

  ---

  播放段落

  Activity 2: Quadratic Methods
  ::活动2:赤道方法

  播放段落

  Some polynomials take the form of a quadratic equation even though they have a degree higher than 2.
  ::有些多面形的方程是二次方程,即使其学位高于2。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Factor  $\begin{align*}x^4 – 81\end{align*}$
  ::系数 x4-81

  播放段落

  This problem may not look like the difference of squares, but think back to the basic exponent rules. M ultiplying  $\begin{align*}x^2\end{align*}$   by itself will produce the following:
  

  $$\begin{align*}{(x^2)}^{2} = x^2 \cdot x^2 = {x}^{2+2} = x^4.\end{align*}$$
  ::这个问题可能看起来不像方形的差别, 而是回想基本引言规则。 乘以 x2 本身将产生以下结果 (x2) 2=x2x2=x2+2=x4 。

  播放段落

  Based on this, it can be stated that  $\begin{align*}\sqrt{x^4} = x^2\end{align*}$   and likewise that  $\begin{align*}{(x^2)}^{2} = x^4.\end{align*}$   The number  81 can also be rewritten as  $\begin{align*}9^2\end{align*}$   or  $\begin{align*}3^4.\end{align*}$   This exponent property allows you to rewrite the original polynomial as a difference of two squares:
  ::基于这一点,可以说"x4=x2",同样,(x2)2=x4。数字81也可以被改写为92或34。此引号属性允许您重写原多义,作为两个方形的差数:

  播放段落

  $$\begin{align*}x^4 – 81 = {(x^2)}^{2} – {(3^2)}^{2}\end{align*}$$
  ::x4-81=(x2)2-2-(32)2

  播放段落

  Now  factor the expression using the difference of two squares,  resulting in the following:
  ::现在用两个方形的差数乘以表达式,得出以下结果:

  播放段落

  $$\begin{align*}{(x^2)}^{2} – {(3^2)}^{2} &= (x^2 + 3^2)(x^2 - 3^2)\\ &= (x^2 + 9)(x^2 - 9)\end{align*}$$
  :x2)2-(32)2=(x2+32)(x2-32)=(x2+9)9(x2-9)

  播放段落

  L ook at the answer to ensure that it cannot be factored further. The expression  $\begin{align*}(x^2 + 9)\end{align*}$  cannot be factored further. However, the expression  $\begin{align*}(x^2-9)\end{align*}$   which can also be written as  $\begin{align*}(x^2 - 3^2)\end{align*}$  is the difference of two squares and can be factored further.
  ::查看答案以确保它不能被进一步考虑。 表达式( x2+9) 无法进一步考虑。 但是, 也可以写成为( x2 - 32) 的表达式( x2 - 9) 是两个方形的区别, 可以进一步考虑 。

  播放段落

  $$\begin{align*}(x^2 - 3^2) = (x+3)(x-3)\end{align*}$$
  :x2-32)=(x+3)(x-3)

  播放段落

  Answer:   $\begin{align*}(x^2 + 9)(x+3)(x-3)\end{align*}$
  ::答复: (x2+9) (x+3)(x-3)

  播放段落

  A degree 4 polynomial is known as a quartic . Some quartics can be factored using quadratic methods.
  ::4°4 多元度被称作夸度,有些夸度可使用二次方位法进行计算。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Factor  $\begin{align*}x^4 - 14x^2 - 95\end{align*}$
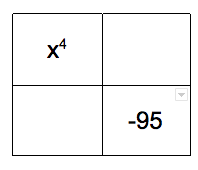
  ::系数 x4 - 14x2 - 95

  播放段落

  The trinomial above is degree 4; however, since the degrees of the trinomial have the ratio 2:1:0,  it can be factored like a regular quadratic  trinomial. U se an area model to confirm this.
  ::以上三个等级为4级; 但是, 由于三等等级的比值为2: 1 : 0, 可以用正常的四等三角等级来计算。 使用区域模型来确认这一点 。

  

  播放段落

  B egin by looking for terms that multiply to  $\begin{align*}x^4.\end{align*}$   The first factors to be  considered  are $\begin{align*}x^2 \cdot x^2.\end{align*}$   More  combinations  would need to be considered if the $\begin{align*}a\end{align*}$  -coefficient is greater than 1.
  ::开始寻找乘以 x4 的术语。 需要考虑的第一个因素是x2xx2。 如果系数大于1, 则需要考虑更多的组合。

  

  播放段落

  Lastly,  look for  factors of -95 that add to -14
  ::最后,寻找增加 -14的-95因素

  

  播放段落

  F ill the factors highlighted above into the table and use them to display the answer.
  ::将上面强调的因素填入表格,并用它们来显示答案。

  

  播放段落

  Answer:   $\begin{align*}x^4 - 14x^2 - 95 = (x^2 + 5)(x^2 - 19).\end{align*}$
  ::答复: x4-14x2-95=(x2+5)(x2-19)。

  播放段落

  This could also have been done using decomposition or other quadratic factoring approaches. A lways look at the remaining binomials and factor them further if possible. In this case, neither binomial can be factored further.
  ::也可以使用分解或其他二次系数法来做到这一点。 总是看剩下的二进制,如果可能的话,再进一步考虑它们。 在这种情况下,两进制都不能被进一步考虑。

   

  ---

  播放段落

  Activity 3: Grouping
  ::活动3:分组

  播放段落

  When a polynomial has 4 terms, one method that could be used to factor it  is a strategy called grouping. This method of factoring is very similar to the decomposition strategy presented in Factoring Quadratic Expressions .
  ::当多面体有 4 个术语时, 一种可以用来计算它的方法就是一个叫成组合的战略。 这种计算法非常相似于计算二次曲线表达式中的分解策略 。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Factor  $\begin{align*}5x^3 + 15x^2 - 7x - 21\end{align*}$
  ::5x3+15x2-7x-21

  播放段落

  The steps for grouping are as follows:
  ::分类步骤如下:

  播放段落

  1. Make two groups of two terms and factor out the greatest common factor from each group.
  ::1. 将两个任期分成两组,并将每一组的最大共同因素考虑在内。

  播放段落

  Usually, the first two terms and the last two terms are grouped, but this does not always need to be the case. You may want to start with the first two and try another grouping if it does not work.
  ::通常,前两个任期和后两个任期被分组,但并不一定需要这样。如果前两个任期不起作用,您可能要从头两个开始尝试另一个分组。

  播放段落

  $\begin{align*}(5x^3 + 15x^2)+ (- 7x - 21) = 5x^2 (x + 3) - 7(x + 3)\end{align*}$
  :5x3+15x2)+(-7x-21)=5x2(x+3)-7(x+3)

  播放段落

  2. If the resulting polynomials are the same after factoring out a GCF, factor out the greatest common factor from the result of step 1.
  ::2. 如果在计入一个全球合作框架之后,所产生的多种族因素相同,则将第1步所产生的最大共同因素考虑在内。

  播放段落

  In this case, the greatest common factor of  $\begin{align*}5x^2 (x + 3)\end{align*}$   and  $\begin{align*}-7(x + 3)\end{align*}$   is  $\begin{align*}(x + 3).\end{align*}$
  ::在这种情况下,5x2(x+3)和-7(x+3)的最大共同系数是(x+3)。

  播放段落

  $\begin{align*}5x^2 (x + 3) - 7(x + 3) = (5x^2 - 7)(x + 3)\end{align*}$
  ::5x2(x+3)-7(x+3)=(5x2-7)(x+3)

  播放段落

  As with the polynomials from the previous activities , always check the answers to make sure that they are fully factored. In this case, the answer cannot be factored further.
  ::与以往活动的多边协议一样,总是要检查答案以确保它们被充分考虑。 在这种情况下,答案无法进一步考虑。

  播放段落

  Answer:  $\begin{align*}(5x^2 - 7)(x + 3)\end{align*}$  
  ::答复5x2-7)(x+3)

   

  ---

  播放段落

  Warm-Up: Review Questions
  ::暖暖:审查问题

   

  播放段落

   Summary  
  ::摘要

  播放段落
  • A polynomial is prime if it cannot be written as a product of polynomials with a lower degree.
    ::如果多面体不能作为低度多面体的产物写成,那么多面体是首要的。
  播放段落
  • A cubic is a third-degree polynomial that can be written in the form of  $\begin{align*}ax^3+bx^2+cx+d.\end{align*}$  
    ::立方体是三度多元度,可以用x3+bx2+cx+d的形式写成。
  播放段落
  • A quartic is a fourth-degree polynomial.
    ::石度是四度多元度。
  播放段落
  • To factor higher-degree polynomials  using the  grouping method:
    ::使用分组方法的较高度多数值系数:

  播放段落
  1. Make two groups of two terms and factor out the greatest common factor from each group.
     ::将两个任期分成两组,并将每一组的最大共同因素考虑在内。
  播放段落
  2. If the resulting polynomials are the same after factoring out a GCF, factor out the greatest common factor from the result of step 1.
     ::如果在计入一个全球合作框架之后,所产生的多种族因素相同,则将第1步的结果中最大的共同因素考虑在内。