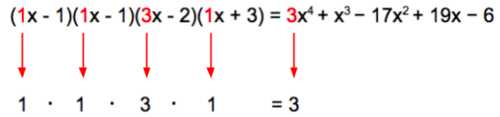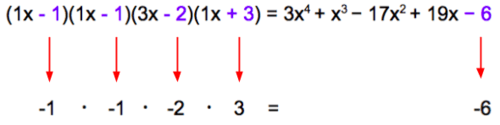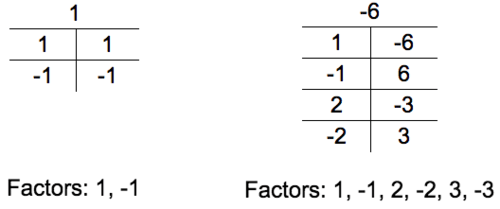Course: 4.2 以乘数为因数的高学位多元体-interactive

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 保理高等学位聚合体

Collapse Expand
保理高等学位聚合体
Lesson Objectives
::经验教训目标

Factor with degree greater than two using long division .
::使用长分离法的度大于2的系数。

Find possible factors of a polynomial with a degree greater than two.
::找到一个大于两个多面体的多面体的可能因素。

Use the rational roots theorem and division to find the factors of a polynomial with a degree greater than two.
::使用理性根理论和分解来找到一个大于2度的多元论因素。

Factor polynomials with degree greater than two using the sum of cubes and the difference of cubes.
::以立方体和立方体之差之和计算,倍数大于2倍的系数倍数。

Introduction: Volume
::导言:数量

You live in a world where you can print almost anything you can dream up. If you have ever used a 3D design program, you are likely familiar with the idea of scale. When a 3D model is created, the sides and edges of the shape are defined relative to the scale. For example, one side may be one unit long, and another side might be two units long. This unit is the scale factor; the unit can be one inch long or 5 feet long depending on the size and capabilities of the printer. The length of the unit may change, but one side will always be double the other.
::您生活在一个几乎可以打印任何你能梦想到的东西的世界中。如果您曾经使用过 3D 设计程序, 您很可能熟悉比例尺的概念。当创建了 3D 模型时, 形状的侧边和边缘会相对于比例尺来定义。例如, 一方可能是一单位长, 另一边可能是两单位长。这个单位是比例尺系数; 单位可以是一英寸长或五英尺长, 取决于打印机的大小和能力。单位的长度可能会改变, 但一方总是加倍。

INTERACTIVE

Volume

Move the orange point in order to change the dimensions of the rectangular prism.
::移动橙色点以改变矩形棱柱的维度。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Find a rectangular prism near you and use the interactive to model that prism. Observe how the relationships between sides affect the volume of the shape. What is the volume of the shape? What are the factors of this polynomial?
::在您附近找到一个矩形棱镜, 并使用交互式模型模拟这种棱镜。观察两边之间的关系如何影响形状的体积。形状的体积是多少? 这个多面性的因素是什么 ?

Activity 1: Factor Using Division
::活动1:要素使用司

As shapes get more complicated, so do the polynomials representing their properties .
::随着形状变得更加复杂,代表其属性的多面体也变得更加复杂。

Use the interactive to explore the dimensions of a cube with a cutout.
::使用互动来探索带有剪切的立方体的维度。

INTERACTIVE

Factor Using Division

This cube container has sides which have length $s.$

::这个立方体容器的侧面长度为s。

Move the red point to change the value of $a,$ the thickness of the walls.
::移动红点以改变 a 的值, 墙壁的厚度。

Observe how changing $a$ would affect the volume of the cutout.
::观察一个变化会如何影响切口量。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

What are the factors of the polynomial in the interactive? What do they represent in context?
::互动中的多元因素是什么?在上下文中它们代表什么?

T he interactive above displays a polynomial that cannot be factored using quadratic methods. However, assuming you know at least one factor, you can factor the polynomial using long division. In , long division was used to rewrite a polynomial as the product of factors.
::上面的交互显示一个无法用二次计算法计算成的多元值。但是, 如果您知道至少一个因素, 您可以用长的分割法来计算多元值。在中, 长的分割法被用来重写一个多元值作为因子的产物。

Example
::示例示例示例示例

Divide $\begin{aligned} 3 x^{4} + x^{3} - 17 x^{2} + 19 x - 6 \end{aligned}$ by $\begin{aligned} x^{2} - 2 x + 1 \end{aligned}$
::除以 3x4+x3 - 17x2+19x- 6 x2 - 2x+1

The long division would play out as follows:
::长期划分如下:

Since $\begin{aligned} x^{2} - 2 x + 1 \end{aligned}$ goes into $\begin{aligned} 3 x^{4} + x^{3} - 17 x^{2} + 19 x - 6 \end{aligned}$ with no remainder $\begin{aligned} 3 x^{2} + 7 x - 6 \end{aligned}$ times, t he quotient can be factored as follows:
::由于 x2 - 2x+1 进入 3x4+x3 - 17x2+19x-6 ,且无余量 3x2+7x-6 倍,该商数可以计算如下:

$\begin{aligned} 3 x^{4} + x^{3} - 17 x^{2} + 19 x - 6 = (x^{2} - 2 x + 1) \cdot (3 x^{2} + 7 x - 6) \end{aligned}$

::3x4+x3-17x2+19x-6=(x2-2x+1)__(3x2+7x-6)

However, to ensure that this is the prime factorization, check to see if each factor can be factored further. In this case, knowledge of factoring quadratic trinomials can be used to factor the factors of the original expression .
::然而,为了确保这是首要因素化,请检查是否每个因素都可进一步因素化,在这种情况下,可以利用对四边三角因素因素因素的认知来计算原表达式因素。

  •   $\begin{aligned} x^{2} - 2 x + 1 \end{aligned}$ will factor to $\begin{aligned} (x - 1) (x - 1) \end{aligned}$
::• x2-2x+1乘以(x-1)(x-1)

  •   $\begin{aligned} 3 x^{2} + 7 x - 6 \end{aligned}$ will factor to $\begin{aligned} (3 x - 2) (x + 3) \end{aligned}$
::• 3x2+7x-6乘以3x-2(x+3)

Since no factors can be factored further, use these factors to write the prime factorization of $\begin{aligned} 3 x^{4} + x^{3} - 17 x^{2} + 19 x - 6. \end{aligned}$
::由于无法进一步考虑因素,利用这些因素来写出3x4+x3-17x2+19x-6的主要因数。

$\begin{aligned} 3 x^{4} + x^{3} - 17 x^{2} + 19 x - 6 = (x - 1) \cdot (x - 1) \cdot (3 x - 2) \cdot (x + 3) \end{aligned}$

::3x4+x3-17x2+19x-6=(x-1)__(x-1)__(x-1)__(3x-2)__(x+3)

Answer: $\begin{aligned} (x - 1)^{2} \cdot (3 x - 2) \cdot (x + 3) \end{aligned}$
::答复: (x-1)2_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Use long division to factor the polynomials in the questions below.
::使用长的分隔法在下面的问题中乘以多面性。

Activity 2: The Rational Factors Theorem
::活动2:理性因素理论

In the example above, you were able to fully factor a fourth-degree polynomial when given one of the factors, but how would you factor a polynomial if you weren’t given any factors?
::在上述例子中,当给出一个因素时,你完全可以考虑四度多位数,但如果你没有给出任何因素,你又如何考虑多位数?

B egin by considering how to write the prime factorization of numbers. Consider the number 786, you aren’t given any factors, but you could use tricks and strategies to help get started. For example, 786 is even, so you know that 2 is a factor. D ividing 786 by 2 will result in a quotient of 393. The factor 2 is prime and cannot be factored further. However, 393 is divisible by 3 because 3 + 9 + 3 = 15 is a multiple of 3. Dividing 393 by 3 will produce 131, which is prime. Now that all the prime factors have been obtained, write the prime factorization:
::开始考虑如何写入数字的质因数。想想数字 786, 您没有给出任何因素, 但是您可以使用技巧和策略来帮助启动。比如, 786 是平的, 所以您知道 2 是一个因数。将786 分解为 2 将得出393 的商数。系数 2 是质数, 无法进一步计算。但是, 393 可除以 3 3 , 因为 3 + 9 3 + 3 = 15 乘以 3 。分解 393 和 3 将产生 131 个, 这才是质数。现在所有主要因数都已获得, 写入主要因数 :

$\begin{aligned} 786 = 2 \cdot 3 \cdot 131 \end{aligned}$

By examining the structure of a polynomial, you can find hints about potential binomial factors. The leading coefficient of the unfactored polynomial is the product of each of the leading coefficients of the binomial factors.
::通过研究多元系数的结构,您可以找到潜在二进制因素的提示。未考虑的多元系数主要系数是二进制因素中每个主要系数的产物。

The constant of the unfactored polynomial is the product of each of the constants of the binomial factors.
::无因数多元值的常数是二进制因素的每个常数的产物。

Rational Factor s
::理性因素

If $\begin{aligned} p x - q \end{aligned}$ is a factor of a polynomial with integer coefficients, $\begin{aligned} p \end{aligned}$ is a factor of the leading coefficient, and $\begin{aligned} q \end{aligned}$ is a factor of the constant.

Example
::示例示例示例示例

Find all potential factors of $\begin{aligned} x^{3} - 9 x^{2} + 5 x - 6 \end{aligned}$
::查找 x3- 9x2+5x- 6 的所有潜在因数

Any potential binomial factors of $\begin{aligned} 1 x^{3} - 9 x^{2} + 5 x - 6 \end{aligned}$ will have a leading coefficient that is a factor of 1, and a constant that is a factor of -6.
::1x3-9x2+5x-6 的任何潜在二进制系数都将有一个主要系数,即1系数,一个常数,即 -6系数。

For this polynomial, any factors of the form $\begin{aligned} p x - q \end{aligned}$ will have a leading coefficient of either 1 or -1 and a constant of 1, -1, 2, -2, 3, or -3. All possible factors will be the combinations of these factors.
::对于这一多元性,形式px-q的任何因素的主要系数为1或-1,常数为1、1、2、2、3或3。所有可能的因素都将是这些因素的结合。

Answer: Possible factors: $\begin{aligned} (1 x + 1), \end{aligned}$    $\begin{aligned} (1 x - 1), \end{aligned}$    $\begin{aligned} (1 x + 2), \end{aligned}$    $\begin{aligned} (1 x - 2), \end{aligned}$    $\begin{aligned} (1 x + 3), \end{aligned}$    $\begin{aligned} (1 x - 3), \end{aligned}$    $\begin{aligned} (- 1 x + 1), \end{aligned}$    $\begin{aligned} (- 1 x - 1), \end{aligned}$    $\begin{aligned} (- 1 x + 2), \end{aligned}$    $\begin{aligned} (- 1 x - 2), \end{aligned}$    $\begin{aligned} (- 1 x + 3), \end{aligned}$    $\begin{aligned} (- 1 x - 3) \end{aligned}$
::答复:可能的因素:1x+1,1x-1,1x-1,1x+2,1x-2,1x-2,1x+3,1x-3),(1x-3),(-1x+1),(-1x-1),(-1x-1),(-1x+2),(-1x-2),(-1x+3),(-1x-3)

Answer the questions below to practice finding potential factors for a higher degree polynomial.
::回答下述问题,以便从实践中找出造成更高学位多元性的潜在因素。

Activity 3: Prime Factorization
::活动3:主要因素化

It is now time to put all the pieces together and find the prime factorization of a polynomial.
::现在是将所有碎片拼凑在一起,找到多元性的主要因素的时候了。

Example
::示例示例示例示例

Find the prime factorization of $\begin{aligned} 2 x^{3} + 5 x^{2} - 4 x - 3. \end{aligned}$
::查找 2x3+5x2-4x-3 的主要乘数。

The polynomial $\begin{aligned} 2 x^{3} + 5 x^{2} - 4 x - 3 \end{aligned}$ has 4 terms so grouping could be attempted. However, you should realize pretty quickly that taking a greatest common factor out of any grouping of two terms will not produce expressions that can be combined. Since quadratic methods are off the table, find the possible rational factors . The factors of 2 are 1, -1, 2, -2 and the factors of -3 are 1, -1, 3, -3. This gives you the following possible factors:
::多角度 2x3+5x2-4x-3 有 4 个术语, 因此可以尝试分组。但是, 您应该非常快地意识到, 从任何组合的两个术语中取出一个最大的共同系数不会产生可以组合的表达方式。由于四边形方法不在桌面上, 请找到可能的合理因素。 2 的系数为 1 - 1, 2, 2 - 2, 3 的系数为 1, 1, 1, 3, 3 。这为您提供了以下可能的因素 :

Possible factors: $\begin{aligned} (1 x + 1), \end{aligned}$    $\begin{aligned} (1 x - 1), \end{aligned}$    $\begin{aligned} (1 x + 3), \end{aligned}$    $\begin{aligned} (1 x - 3), \end{aligned}$ $\begin{aligned} (- 1 x + 1), \end{aligned}$    $\begin{aligned} (- 1 x - 1), \end{aligned}$ $\begin{aligned} (- 1 x - 1), \end{aligned}$ $\begin{aligned} (- 1 x + 3), \end{aligned}$ $\begin{aligned} (- 1 x - 3), \end{aligned}$    $\begin{aligned} (2 x + 1), \end{aligned}$    $\begin{aligned} (2 x - 1), \end{aligned}$    $\begin{aligned} (2 x + 3), \end{aligned}$    $\begin{aligned} (2 x - 3), \end{aligned}$    $\begin{aligned} (- 2 x + 1), \end{aligned}$    $\begin{aligned} (- 2 x - 1), \end{aligned}$    $\begin{aligned} (- 2 x + 3), \end{aligned}$    $\begin{aligned} (- 2 x - 3) \end{aligned}$
::可能的因素:1x+1,1x-1,1x-1,1x+3,1x-3),(-1x+1),(-1x-1),(-1x-1),(-1x-1),(-1x+1),(-1x+3),(-2x+1),(2x+1),(2x+3),(-2x+3),(-2x+1),(-2x-1),(-2x+3),(-2x+3),(-2x+1),(-2x+3),(-2x+3)

From here, guess potential factors and use either synthetic division or long division to determine if the binomial divides the polynomial with no remainder. It is best to start with the easiest factors to divide when working your way through them. B egin by using synthetic division to check the factor $\begin{aligned} (x + 1) . \end{aligned}$
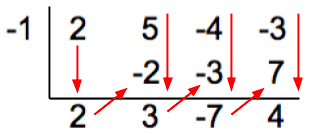
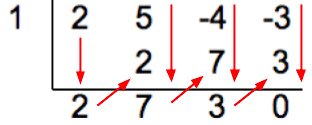
::从这里猜测潜在因素, 并使用合成分裂或长的分裂来确定二元体是否将多元体除以没有剩余部分。最好先从最简单的因素开始, 在您通过这些因素时进行分裂。开始使用合成分裂来检查系数( x+1 ) 。

As you can see above, the factor $\begin{aligned} (x + 1) \end{aligned}$ has a remainder of 4, so it is not a factor of $\begin{aligned} 2 x^{3} + 5 x^{2} - 4 x - 3. \end{aligned}$ Next, check the possible factor $\begin{aligned} (x - 1) . \end{aligned}$
::如上文所示,系数(x+1)的剩余值为4,因此不是2x3+5x2-4x-3的系数。下一步,检查可能的系数(x-1)。

The factor $\begin{aligned} (x + 1) \end{aligned}$ divides $\begin{aligned} 2 x^{3} + 5 x^{2} - 4 x - 3 \end{aligned}$ with a remainder of 0; thus, it is a factor. From the synthetic division, the following can be stated :
::系数(x+1)除以 2x3+5x2-4x-3,其余部分为0;因此,这是一个系数。

$\begin{aligned} 2 x^{3} + 5 x^{2} - 4 x - 3 = (x - 1) (2 x^{2} + 7 x + 3) \end{aligned}$

::2x3+5x2-4x-3=(x-1)(2x2+7x+3)

The next step is to factor the quadratic equation $\begin{aligned} 2 x^{2} + 7 x + 3. \end{aligned}$ You have learned several strategies for factoring quadratics; in this case, use decomposition.
::下一步是乘以二次方程 2x2+7x+3。你学到了几种计算二次方程的策略; 在这种情况下, 使用分解法。

1. Separate the $\begin{aligned} x \end{aligned}$ term into the sum of two terms that add up to the original $\begin{aligned} x - \end{aligned}$ term but multiply to the product of the $\begin{aligned} x^{2} \end{aligned}$ term and the constant.
::1. 将x术语分为两个词的总和,两个词加起来等于原来的x期限,但乘以x2术语和常数的产物。

The product of the $\begin{aligned} x^{2} \end{aligned}$ term and the constant is $\begin{aligned} 2 x^{2} \cdot 3 = 6 x^{2} . \end{aligned}$ You know that the two terms that add up to $\begin{aligned} 7 x \end{aligned}$ but multiply to $\begin{aligned} 6 x^{2} \end{aligned}$ will each have an $\begin{aligned} x \end{aligned}$ so focus on the coefficients. The factors of $\begin{aligned} 6 x^{2} \end{aligned}$ that add up to $\begin{aligned} 7 x \end{aligned}$ are $\begin{aligned} 1 x \end{aligned}$ and $\begin{aligned} 6 x, \end{aligned}$ so replace the $\begin{aligned} x \end{aligned}$ term with the sum of these factors:
::x2 术语和常数的产物为 2x2222}3=6x2 。你知道,两个共7x但乘以 6x2 的术语中,每个术语都会有一个x如此以系数为重点。 6x2 共7x的系数是 1x 和 6x, 所以用这些因素的总和替换 x :

$\begin{aligned} 2 x^{2} + 7 x + 3 = 2 x^{2} + 1 x + 6 x + 3 \end{aligned}$

::2x2+7x+3=2x2+1x+6x+3

2. Take the greatest common factor out of the first two terms and last two terms.
::2. 在前两个任期和最后两个任期中采用最大的共同因素。

The greatest common factor of the first two terms, $\begin{aligned} 2 x^{2} \end{aligned}$ and $\begin{aligned} - 1 x, \end{aligned}$ is $\begin{aligned} x . \end{aligned}$ The greatest common factor of the last two terms is 3.
::前两个任期(2x2和-1x)的最大共同系数是x。前两个任期的最大共同系数是3。

$\begin{aligned} 2 x^{2} + 1 x + 6 x + 3 = x (2 x + 1) + 3 (2 x + 1) \end{aligned}$

::2x2+1x+6x+3=x( 2x+1)+3( 2x+1)

You want the value left in each set of terms to be the same after taking out the GCF. You may have to take out a negative to accomplish this.
::您希望每套条款中的剩余值在取出绿色气候基金后保持相同。您可能需要拿出负值来完成此目的。

3. Take the greatest common factor out of the result of step 2.
::3. 从第2步的结果中取出最大的共同因素。

Both $\begin{aligned} x (2 x + 1) \end{aligned}$ and $\begin{aligned} 3 (2 x + 1) \end{aligned}$ have $\begin{aligned} (2 x + 1) \end{aligned}$ as a common factor , so this can be factored out.
::x( 2x+1) 和 3( 2x+1) 都有一个共同系数(2x+1) , 因而可以将这个系数算出来。

$\begin{aligned} x (2 x + 1) + 3 (2 x + 1) = (2 x + 1) (x + 3) \end{aligned}$

::x(2x+1)+3(2x+1)=(2x+1)(x+3)

Now write the prime factorization of $\begin{aligned} 2 x^{3} + 5 x^{2} - 4 x - 3. \end{aligned}$
::现在写入 2x3+5x2- 4x- 3 的主因数化。

Answer: $\begin{aligned} 2 x^{3} + 5 x^{2} - 4 x - 3 = (x - 1) (2 x + 1) (x + 3) \end{aligned}$
::答复: 2x3+5x2-4x-3=(x-1)(2x+1)(x+3)

Answer the questions below to practice factoring higher degree polynomials.
::回答以下问题,以实践考虑更高学位多民族学。

Discussion Question : Was it easier or more difficult to factor a binary polynomial? Explain.
::讨论问题:将二进制多元性因素考虑在内是否更容易或更困难?解释一下。

Extension: Sum and Difference of Cubes
::扩展号:立方体的总和和差异

Much like you can use the difference of two squares shortcut to factor polynomials of the form $\begin{aligned} a^{2} - b^{2}, \end{aligned}$ there is also a shortcut for of the form $\begin{aligned} a^{3} + b^{3} and a^{3} - b^{3} . \end{aligned}$ To factor a polynomial of the form $\begin{aligned} a^{3} + b^{3}, \end{aligned}$ use the sum of cubes shortcut.
::类似地,您可以使用两个方形快捷键的差数来计算窗体 a2 - b2 的多数值, 窗体 a3+b3 和 a3 - b3 的快捷键也有一个快捷键来计算窗体 a3+b3 的多数值, 使用立方体快捷键的总和。

Sum of Cubes
::立方体总和

A polynomial of the form $\begin{aligned} a^{3} + b^{3} \end{aligned}$ can be factored to $\begin{aligned} (a + b) (a^{2} - a b + b^{2}) . \end{aligned}$

To factor a polynomial of the form $\begin{aligned} a^{3} - b^{3}, \end{aligned}$ use the difference of cubes shortcut.
::要乘以窗体 a3-b3 的多数值,请使用立方体快捷键的差数。

Difference of Cubes
::立方体差异

A polynomial of the form $\begin{aligned} a^{3} - b^{3} \end{aligned}$ can be factored to $\begin{aligned} (a - b) (a^{2} + a b + b^{2}) . \end{aligned}$

Example
::示例示例示例示例

Factor $\begin{aligned} 8 x^{3} + 27 \end{aligned}$
::8x3+27因数

Once you identify that this is a case of the sum of cubes, determine the cubed roots that represent $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b . \end{aligned}$ The roots in the a and b positions are interchangeable because of the commutative property . However, t he terms in the a and b position for the difference of cubes are not as easily interchangeable.
::一旦确定这是立方体和立方体之和, 确定代表 a 和 b 的立方根。 a 和 b 位置的根可以互换, 因为有通量属性。但是, 立方体差异的a 和 b 位置的词句不那么容易互换。

• a: The cubed root of $\begin{aligned} 8 x^{3} is 2 x . \end{aligned}$
::• a:8x3的立方根为2x。

•   b: The cubed root of 27 is 3.
::• b:27的立方根为3。

You will need to use the sum of cubes formula above because the cubes are being added. Using this formula , the following is obtained:
::您需要使用以上立方体公式的总和, 因为立方体正在被添加。使用此公式, 可以获得以下公式 :

$\begin{aligned} a^{3} - b^{3} & = (a - b) (a^{2} + a b + b^{2}) \\ = ((2 x) - (3)) ((2 x)^{2} + (2 x) (3) + (3)^{2}) \\ = (2 x - 3) (4 x^{2} + 6 x + 9) \end{aligned}$

::a3-b3=(a-b)(a2+ab+b2)=(2x)-(3)(2x)-2+(2x)(3)+(2x)(3)+(3)2)=(2x-3)(4x2+6x+9)

Since neither factor can be factored further, you have the answer.
::因为两个因素都不能进一步考虑,所以你可以回答。

Answer: $\begin{aligned} (2 x - 3) (4 x^{2} + 6 x + 9) \end{aligned}$
::答复2x-3)(4x2+6x+9)

Discussion Questions :
::讨论问题:

How many different ways could you factor $\begin{aligned} x^{6} - y^{6} ? \end{aligned}$
::您可以用多少种不同的方法来乘以 x6 -y6 ?

What other polynomials of the form $\begin{aligned} x^{n} + y^{n} or x^{n} - y^{n} \end{aligned}$ could you extend these formulas to help factor?
::您可以将这些公式扩展至帮助因子的 xn+yn 或 xn-yn 等窗体的其他多数值吗 ?

Use the interactive below to derive the formulas.
::使用下面的交互数据得出公式。

Wrap-Up: Review Questions
::总结:审查问题

Remember This!
::记住这个!

To factor a higher degree polynomial, remove factors using synthetic or long division until you have a quadratic which can be factored or there are no more factors that can be taken out.
::对于更高程度的多元系数,使用合成或长分离法去除各种系数,直到有一个可被系数乘以的二次方位数或没有其他因素可以排除为止。

I f $\begin{aligned} p x - q \end{aligned}$ is a factor of a polynomial with integer coefficient , p is a factor of the leading coefficient, and q is a factor of the constant.
::如果px-q是具有整数系数的多元系数,p是主要系数的一个系数,q是常数的一个系数。

Use the R ational F actors T heorem to find factors of a polynomial that can be divided out.
::使用“理性因素”理论来找出可以分割的多元因素。

S um of cubes states that a polynomial of the form $\begin{aligned} a^{3} + b^{3} \end{aligned}$ can be factored to $\begin{aligned} (a + b) (a^{2} - a b + b^{2}) . \end{aligned}$
::立方体总和表示窗体 a3+b3 的多元值可以乘以(a+b(a2-ab+b2)。

D ifference of c ubes states that a polynomial of the form $\begin{aligned} a^{3} - b^{3} \end{aligned}$ can be factored to $\begin{aligned} (a - b) (a^{2} + a b + b^{2}) . \end{aligned}$
::立方体的差别表明,窗体a3-b3的多元值可以乘以(a-b)(a2+ab+b2)。

Section outline

General

保理高等学位聚合体

Introduction: Volume ::导言:数量

Activity 1: Factor Using Division ::活动1:要素使用司

Activity 2: The Rational Factors Theorem ::活动2:理性因素理论

Rational Factor s ::理性因素

Activity 3: Prime Factorization ::活动3:主要因素化

Extension: Sum and Difference of Cubes ::扩展号:立方体的总和和差异

Sum of Cubes ::立方体总和

Difference of Cubes ::立方体差异

Wrap-Up: Review Questions ::总结:审查问题

Remember This! ::记住这个!

Introduction: Volume
::导言:数量

Activity 1: Factor Using Division
::活动1:要素使用司

Activity 2: The Rational Factors Theorem
::活动2:理性因素理论

Rational Factor s
::理性因素

Activity 3: Prime Factorization
::活动3:主要因素化

Extension: Sum and Difference of Cubes
::扩展号:立方体的总和和差异

Sum of Cubes
::立方体总和

Difference of Cubes
::立方体差异

Wrap-Up: Review Questions
::总结:审查问题

Remember This!
::记住这个!