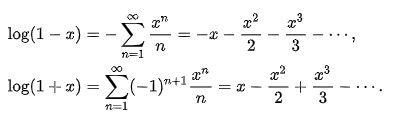5.4 对数-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 对数对数

  Collapse Expand

  对数对数

  Lesson Objectives

  播放段落
  • Understand the characteristics and structure of a logarithm.
    ::理解对数的特性和结构 。
  播放段落
  • Solve equations by converting between exponential form and logarithmic form.
    ::通过指数形式和对数形式之间的转换来解析方程式。
  播放段落
  • Understand the characteristics and structure of a common logarithm.
    ::理解普通对数的特性和结构 。
  播放段落
  • Solve equations using the formula.
    ::使用公式解决方程式。
  播放段落
  • Convert between logarithmic form and natural logarithmic form.
    ::在对数窗体和自然对数窗体之间转换。
  播放段落
  • Solve equations by converting between exponential form and natural logs.  
    ::通过指数形式和自然原木之间的转换来解决方程式问题。

  ---

  播放段落

  Introduction: Going Viral Again
  ::一. 导言:再次恢复活力

  

  播放段落

  Consider  the function   $\begin{align*}f(x)=5^x\end{align*}$   as   a model of the views of a music video $\begin{align*}x\end{align*}$  weeks after being posted.
  ::将函数 f( x) =5x 视为张贴后的音乐视频 x 周视图的模型 。

  播放段落

  The  graph of the function is shown below :
  ::函数图示如下:

  播放段落

  Given the model,  when would the video would get a million views? You can see from the graph that the vi deo  can be expected  to   reach a million views between 8 and 9 days. However, what if you wanted a more accurate estimate? Can you develop a formula or algorithm to produce the $\begin{align*}x\end{align*}$ -value associated with any $\begin{align*}y\end{align*}$ -value?
  ::根据这个模型, 视频什么时候会得到百万次浏览? 您可以从图表中看到, 视频在8天到9天之间将达到百万次浏览。 但是, 如果您想要更准确的估算值, 您可以开发一个公式或算法来生成与任何 Y 值相关的 x 值吗 ?

   

  ---

  播放段落

  Activity 1: Logarithms
  ::活动1:对数

  播放段落

  If you could develop this algorithm, it would be extremely powerful as it could be used to solve any exponential equation.
  ::如果你能开发出这个算法, 它会非常强大,因为它可以用来解答任何指数方程式。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  $\begin{align*}1. \:\:\:&2{}^{3}=a\\ 2. \:\:\:&{b}^{2}=16\\ 3. \:\:\:&7^{c}=49\end{align*}$
  ::1.23=a2.b2=163.7c=49

  播放段落

  All of these problems involve . The  third   in particular  requires you to perform an operation that is the inverse of  an exponent number to an exponent .  This concept exists and is known as a logarithm. By definition, a logarithm is the inverse of an exponent. Logarithms use a specific notation; the  expression   $\begin{align*}{log}_{5}1,000,000\end{align*}$  represents the exponent, $\begin{align*}x,\end{align*}$  in the equation  $\begin{align*}5^x = 1,000,000.\end{align*}$
  ::所有这些问题都涉及.第三个问题特别要求你执行一个操作,即将一个引言号反转成一个引言号。这个概念存在,并被称为对数。根据定义,对数是一个引言的反义。对数使用一个特定的符号;表达式为 5x= 100 000,000 代表方程式中的前言, x 代表 5x= 100,000 。

  播放段落

  In the interactive above,  $\begin{align*}b\end{align*}$  represents the base, $\begin{align*}x\end{align*}$  represents the exponent, and $\begin{align*}a\end{align*}$   represents the resulting product.  The equation $\begin{align*}b^x = a\end{align*}$  is in what is known as exponential form. When  the  equation is written as  $\begin{align*}x={log}_{b}a,\end{align*}$ this is known as logarithmic form. The logarithmic form can be useful in solving for missing parts of an exponential equation and rewriting exponential expressions. S imple logarithms can be solved by converting them to exponential form.
  ::在互动的上面, b 表示基数, x 表示指数, x 表示结果。 方程式 bx=a 以指数形式出现。 当方程式被写成 x=logba 时, 则称为对数形式。 对数形式可用于解决指数方程式缺失的部分, 并重写指数表达式。 简单的对数可以通过将其转换成指数形式来解析 。

   

  播放段落

  Discussion Questions :
  ::讨论问题:

  播放段落
  1. Find the value of  $\begin{align*}x\end{align*}$  in  $\begin{align*}10^x = 1.\end{align*}$  How does this equation help you solve $\begin{align*}{log}_{b}1?\end{align*}$  How can this be useful?
     ::在 10x=1 中查找 x 的值。 此方程式如何帮助您解析 logb1 ? 这如何有用 ?
  播放段落
  2. Find the value of  $\begin{align*}x\end{align*}$  in  $\begin{align*}25^x = 25.\end{align*}$  How does this equation help you solve $\begin{align*}{log}_{b}b?\end{align*}$  How can this be useful?
     ::查找 x 在 25 x = 25 中的值。 此方程式如何帮助您解析logb ? 这如何有用 ?

   

  ---

  播放段落

  Activity 2:  Using Technology to Solve Logarithms
  ::活动2:使用技术解决对数

  播放段落

  A useful application of logarithms is for problems involving half-life, explored in . The ratio of parent isotopes to daughter isotopes very rarely comes out to a whole number half-life. 
  ::对数的有效应用是针对涉及半衰期的问题,这个问题在......中进行了探讨。母同位素与女同位素的比例很少出现在整个半衰期中。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Scientists are trying to date a sample that has a ratio of parent isotope carbon-14 to daughter isotope N14 of 2:3. C arbon-14 has an approximate half-life of 5,700 years.
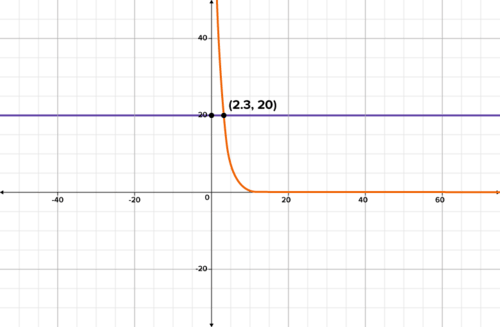
  ::科学家们正在试图找到一个样本,样本中母同位素碳-14与女同位素N14的比例为2:3.碳-14的半衰期约为5,700年。

  播放段落

  Given that the ratio of carbon-14 to nitrogen-14 is 1:4, this means that the ratio of carbon-14 to total is 1:5, and there is 20% carbon-14 in the sample. T here would be 25% carbon-14 after 2 half-lives and 12.5% carbon-14 after 3 half-lives, so the answer is between 2 and 3. The function  $\begin{align*}f(x) = 100\left(\frac{1}{2}\right)^x\end{align*}$  represents the percentage of carbon-14 for any half-life. The function  $\begin{align*}g(x) = 20\end{align*}$  represents the constant 20. The answer will be at the intersection of these two functions.
  ::鉴于碳-14与氮-14之比为1:4,这意味着碳-14与总量之比为1:5,在样本中碳-14的比例为20%。在2半衰期后碳-14为25%,在3半衰期后碳-14为12.5%,因此答案为2至3之间。函数f(x)=100(12)x代表任何半衰期碳-14的百分比。函数g(x)=20代表常数20。答案将在这两个函数的交叉处。

  

  播放段落

  The intersection is approximately at  $\begin{align*}(2.32, 20).\end{align*}$  The $\begin{align*}x\end{align*}$ -value represents the number of half-lives, 2.32, and the $\begin{align*}y\end{align*}$ -value represents the expected percentage of carbon-14 left in the sample at 2.32 half-lives, 20%. Since each half-life is approximately 5,700 years, the answer will be the product of the half-lives and 5,700.
  ::X值表示半衰期数,2.32,20。x值表示样本中的半衰期数,2.32,20。Y值表示样本中的碳-14的预期百分比为2.32半衰期,20%。由于每个半衰期约为5,700年,答案将是半衰期的产物和5,700年。

  播放段落

  Answer:   The sample is approximately 13,224 years old.
  ::答复:抽样大约为13 224岁。

  播放段落

  Use the interactive below to solve  logarithms by graphing.
  ::使用下面的交互方式通过图形化解决对数。

   

  播放段落

  Discussion Question : E valuate   $\begin{align*}\log_{10} 0\end{align*}$  and $\begin{align*}\log_1 10.\end{align*}$  Explain what the solutions mean.
  ::讨论问题:评估log100和log110。解释解决方案的含义。

   

  ---

  播放段落

  Activity 3: Properties of Logarithms
  ::活动3:对数属性

  播放段落

  When typing  $\begin{align*}\log_{5}{16}\end{align*}$  into a calculator, you are asking the question, "5 raised to what power will give you 16?" The approach used by the calculator to answer this question calls upon infinite series like the ones below:
  ::当将log516输入计算器时, 您正在问一个问题, “ 5 将赋予您16 个电源? ” 计算器用来回答这个问题的方法需要无限序列, 如下面的序列 :

  

  播放段落

  The two infinite series get closer to the value from above and below. A similar approach is used to calculate $\begin{align*}π.\end{align*}$  If the series produces an upper-estimate of 5.3417 and a lower-estimate of 5.3415, the answer must contain the digits 5.341. The series is performed until a specific value with an appropriate number of significant digits is produced.
  ::两个无限序列从上到下接近值。在计算 __。如果该序列产生5.3417的上估计值和5.3415的下估计值,答案必须包含数字5.341。该序列在产生适当数目的位数特定值之前进行。

  播放段落

  In the series above, the logarithms don't have a base. When a logarithm does not have a base displayed, the base is assumed to be 10. A base of 10 is  seen often when dealing with the metric system, sound, the Richter Scale, etc. This logarithm is known as the common logarithm .
  ::在以上系列中,对数没有基数。 当对数没有显示基数时, 基数假定为 10 。 当处理公制、 音响、 里氏比例等时, 常看到基数为 10 。 此对数被称为普通对数 。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Evaluate  $\begin{align*}\log{0.01}\end{align*}$  
  ::估量對數=0.01

  播放段落

  The expression  $\begin{align*}\log{0.01}\end{align*}$  means  $\begin{align*}\log_{10}{0.01}.\end{align*}$  This expression can be written in exponential form as  $\begin{align*}10^x = 0.01.\end{align*}$  You may not immediately see it, but when you write the decimal 0.01 as the fraction  $\begin{align*}\frac{1}{100},\end{align*}$  you will need a negative exponent to move the power of 10 to the denominator and  $\begin{align*}100 = 10^2.\end{align*}$   Thus, it can be stated that  $\begin{align*}{10}^{-2}=\frac{1}{100}.\end{align*}$  
  ::表达式 log\\ 0.01 表示为 log10\\ 0.01 。 此表达式可以以指数形式以 10x= 0.01 表示, 您可能无法立即看到它, 但是当您将小数 0.01 写为 1100 分数时, 您需要负引号才能将 10 的功率移动到分母和 100= 102. 。 因此, 可以说是 10- 2= 1100 。

  播放段落

  Answer:  $\begin{align*}\log{0.01} = -2 \end{align*}$   
  ::答复:log@0.01%2

  播放段落

  Some calculators have a function for  $\begin{align*}\log_{b}{a};\end{align*}$  however, many simple calculators only have a  $\begin{align*}\log{a}\end{align*}$  button. To find  $\begin{align*}\log_{b}{a}, \end{align*}$  you will need to use the change of base formula.
  ::有些计算器对logba有一个函数; 然而, 许多简单的计算器只有一个logça按钮。 要找到logba, 您需要使用基公式的更改 。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Solve for  $\begin{align*}x:\end{align*}$   $\begin{align*}4{}^{x}=256\end{align*}$
  ::解决 x: 4x=256

  播放段落

  Once an exponential equation is written in logarithm form, separate the base and product according to the formula below.
  ::一旦指数方程式以对数形式写成,则根据以下公式将基数和产品分开。

  播放段落

  Change of Base Formula
  ::基基公式变动

  $\begin{align*}\log_{b}{(x)}=\frac{\log{(x)}}{\log{(b)}}\end{align*}$  

  播放段落

  This formula will allow you to solve a logarithm with only a $\begin{align*}\log{a}\end{align*}$  button.  This formula will be derived once you are more familiar with .
  ::此公式将允许您只用对数按钮来解析对数。 一旦您更熟悉此公式, 此公式将会被导出 。

  播放段落

  $$\begin{array}{rl}{4}^x& =256\\ \\ x& ={\log }_{4}256\\ \\ x& =\frac{\log 256}{\log 4}\\ \\ x& =\frac{2.408}{0.602}\\ \\ x& =4\end{array}$$

  $$\begin{align*}4^x&=256\\\\ x&=\log_{4}{256}\\\\ x&=\frac{\log{256}}{\log{4}}\\\\ x&=\frac{2.408}{0.602}\\\\ x&=4\end{align*}$$
  ::4x=256x=log4}256x=log*256log*4x=2.4080.602x=4

  播放段落

  Answer: 4
  ::答复:4

    

  ---

  播放段落

  Activity 4: Natural Log
  ::活动4:自然日志

  播放段落

  In the previous section, Functions  introduced the  exponential constant $\begin{align*}e.\end{align*}$   You were asked the following question:
  ::在上一节中,函数引入指数常数 e。 您被问到以下问题:

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Population growth can be modeled using the formula  $\begin{align*}P={P}_{0}\cdot{e}^{rt}\end{align*}$  where  $\begin{align*}{P}_{0}\end{align*}$  is the initial population , $\begin{align*}r\end{align*}$  is the rate of growth, and $\begin{align*}t\end{align*}$  is the time in years. The rate of growth of the human population is approximately 1.1%. Approximately how long will it take for the population to double? 
  ::可以用P=P0的公式来模拟人口增长。 P=P0是最初的人口,r是增长率, t是年中的时间。 人口增长率约为1.1 % 。 人口翻一番需要多长时间?

  播放段落

  You  were able to get an answer by guessing and checking, but now that you know about logarithms, it is possible to get a more exact answer. You also saw that regardless of the starting population, the amount of time would be the same. M ake  $\begin{align*}P_{0} = p \end{align*}$  and  $\begin{align*}P = 2p.\end{align*}$  Substitute 1.1% for $\begin{align*}r\end{align*}$  as a decimal.
  ::您通过猜测和检查获得了答案, 但既然您知道对数, 有可能得到更准确的答案。 您也看到, 无论初始人口多少, 时间数量都是一样的 。 make P0=p 和 P=2p。 以小数表示 r 的替代值 1. 1% 。

  播放段落

  $$\begin{align*}2p=p\cdot{e}^{0.011t}\end{align*}$$
  ::2p=pe0.011t

  播放段落

  M ove $\begin{align*}p\end{align*}$  to the left side using division  to isolate the exponent.
  ::p 移动到左侧, 使用“ 分区” 分隔出处 。

  播放段落

  $$\begin{align*}2p&=\:p\cdot{e}^{0.011t}\\ \div p & \:\:\div p\\ \hline \frac{2p}{p} &= {e}^{0.011t}\\\\ 2 &= {e}^{0.011t}\\\end{align*}$$
  ::2p=pe0.011tpp2pp=e0.011t2=e0.011t

  播放段落

  W rite this as a logarithm to solve for $\begin{align*}t.\end{align*}$  However, there is one issue, what's the base? In this case, the base is  $\begin{align*}e.\end{align*}$
  ::将此写为 t 的对数 。 但是, 有一个问题, 基数是什么 ? 在这种情况下, 基数是 e 。

  播放段落

  $$\begin{align*}log_{e}{2}=0.011t\end{align*}$$
  ::loge2=0.011t loge2=0.011t

  播放段落

  You likely do not know the power of $\begin{align*}e\end{align*}$   that equals 2 off the top of your head. Use  a calculator to help figure it out. Exponential functions with  $\begin{align*}e\end{align*}$  are so common in the real world that  $\begin{align*}\log_{e}\end{align*}$  has  a special button on most calculators. This button is called the natural logarithm and is abbreviated as  $\begin{align*}ln.\end{align*}$
  ::您可能不知道 e 的功率等于您头顶上的 2 。 使用计算器来帮助解析它。 在现实世界中, e 的指数函数非常常见, loge 在大多数计算器上都有一个特殊的按钮。 这个按钮被称为自然对数, 缩写为 In 。

  播放段落

     The Natural Logarithm
  ::自然对数

  $\begin{align*}\log_{e}{x}=\ln{x}\end{align*}$  

  播放段落

  Since  $\begin{align*}\ln{2} \approx 0.693,\end{align*}$   s ubstitute this into  the equation.
  ::从In20.693开始 把这个换成方程式

  播放段落

  $$\begin{align*}0.693&=\:0.011t\\ \div 0.011& \:\:\div 0.011\\ \hline 63 &= t\end{align*}$$
  ::0.693=0.011t 0.011 0.01163=t

  播放段落

  Answer:   The human population doubles approximately every  63 years at the current growth rate.
  ::答复:按照目前的增长率,人口大约每63年翻一番。

   

  播放段落

  Discussion Question : How could you solve a natural log equation using a graph instead of the $\begin{align*}\ln x\end{align*}$  button. Use the interactive below to check your answer.
  ::讨论问题:您如何用图形而不是 Inx 按钮来解析自然日志方程式。 请使用下面的交互键来检查您的答案 。

   

   

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题

   

  播放段落

     Summary
  ::摘要

  播放段落
  • $\begin{align*}b^x=a\end{align*}$  can be written as  $\begin{align*}\log_b a=x.\end{align*}$
    ::bx=a 可以用logba=x 写入 。
  播放段落
  • The  common logarithm has a base of ten and can be written as  $\begin{align*}\log_{10}x \:\text{ or } \log x.\end{align*}$  
    ::普通对数以 10 为基数, 可以写成对数 10 或对数 。
  播放段落
  • The change of base formula is  $\begin{align*}\log_b(x)=\frac{log(x)}{log(b)}.\end{align*}$  
    ::基公式的更改为对数b(x)=log(x)log(b)。
  播放段落
  • The natural logarithm is in the form  $\begin{align*}\ln x.\end{align*}$  
    ::自然对数以In_x的形式出现。