Course: 7.2 弧度-interactive

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

弧度

Lesson Objectives
::经验教训目标

Understand of an angle as the length of the arc on the unit circle subtended by the angle.
::将角度理解为单位圆的弧长度。

Convert between degree and radians.
::在度与弧度之间转换。

Relate angles between 0 and 2 π to their co-terminal angles.
::将0和2之间的角与其共同终点角相对应。

Introduction: Discovering Radians
::导言:发现雷达

In the previous section, Revisiting Right Angle Trigonometry, you used degrees to represent an angle. One example involved expressing the angle at which a train moves relative to flat ground. In addition to degrees, another commonly used unit of angle measure is gradient. Gradient works similarly to the idea of slope where it represents a ratio of the rise to the run. A gradient is commonly written using a percentage. A grade of 1% means a ratio of 1:100, which could mean a rise of 1 foot for a run of 100 feet. Another way to express the measure of an angle is using radians.
::在上一节,即右角重现三角度数中,您使用度数代表角度。一个例子是显示列车相对于平地移动的角度。除了度数外,另一个常用角度单位是梯度。渐变工作与斜度概念相似,斜度代表升幅与运行量之比。斜度通常使用百分比写成。1%的等级为1:100,这意味着100英尺的运行量上升1英尺。另一种表示角度的方法是使用弧度。

Use the interactive below for an introduction to this concept.
::使用下文互动部分来介绍这一概念。

Discussion Question: How does writing the angle in terms of the radius make it easier to find the ? Provide evidence to support your answer. Does the same logic apply when finding the area of an arc sector?
::讨论问题:以半径表示的角度写字如何更容易找到 ?提供证据支持您的答复。在寻找弧扇区区域时,是否适用同样的逻辑?

Activity 1: Introduction to Radians
::活动1:瑞迪亚人介绍

T he term radian is used to describe the measure of that central angle (also called 1 rad ) in terms of the length of the radius. An angle with a measure of 1 rad would correspond to an arc with a measure equal to the radius. An angle with a measure of 2 rad would correspond to an arc measure twice as long as the radius. As you saw in the interactive above, f or any circle, it takes approximately 6.3 radius lengths to wrap around the circumference, which is approximately $\begin{align*}2\pi \end{align*}$ . Therefore, 360° around a circle is equivalent to $\begin{align*}2\pi\end{align*}$ radians, and $\begin{align*}\pi \end{align*}$ radians = 180°.
::弧度一词用于用半径长度来描述该中央角(也称为1 rad)的测量值。度量为1 rad 的角与量等于半径的弧相对应。度量为2 rad 的角相当于半径的两倍于弧度的弧度。正如您在上文互动部分所看到的, 对于任何圆圈,环绕大约需要约6.3 半径的长度。因此, 圆环周围的360°相当于 2 × 弧度, 弧度= 180 °。

Example
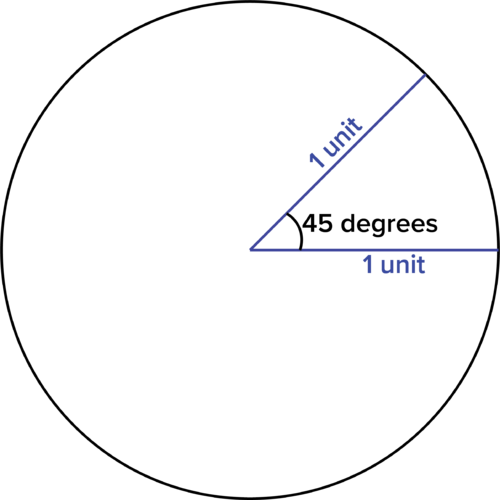
::示例示例示例示例

How would you express 45° in radians?
::你如何用弧度表示45度?

To begin, s ketch a central angle of 45° set inside a circle with a radius of one unit.
::首先,绘制一个45度的中心角, 在一个圆内设置一个圆, 一个单位半径。

T he 45° angle subtends the arc formed on the circle . A 45° angle represents a $\begin{align*}\frac{45}{360} \text{ or } \frac{1}{8} \end{align*}$ fraction of the circle. Since the entire circle can be expressed as a rotation of $\begin{align*}2 \pi,\end{align*}$ a 45° angle will be one-eighth of this.
::45 度角小于45 度角为圆上形成的弧值。 A 45 度角代表圆的45360 或 18 度。由于整个圆圈可以以 2 ° 的旋转表示,因此,45 度角将是这个圆圈的八分之一。

\begin{aligned} \frac{1}{8} \cdot 2 π = \frac{2 π}{8} = \frac{π}{4} \end{aligned}

$\begin{align*}\frac{1}{8}\cdot 2 \pi = \frac{2 \pi}{8} = \frac{\pi}{4}\end{align*}$

Answer: $\begin{align*}45° = \frac{\pi}{4} rad\end{align*}$
::答复:454rad

Given that 360° is $\begin{align*}2 \pi\end{align*}$ radians, you can use this to convert any degree measure.
::鉴于360°为2弧度,您可以用此转换任何度量。

Use the quiz below to practice converting degrees to radians.
::使用下面的测验练习将度转换为弧度。

Discussion Question: Write a formula to convert an angle from degrees to radians.
::讨论问题:写一个公式,将角度从度转换为弧度。

Activity 2: Converting Between Radians and Degrees
::活动2:辐射和度之间的转换

Formulas can be used to convert between degrees and radians, however, a quick reference point is to remember that $\begin{align*}\pi = 180°.\end{align*}$ F inding a fraction of 180°, will result in the same fraction of pi.
::公式可用于在度和弧度之间转换,然而,快速参照点是 180 °。找到180 °的分数,就会产生相同的pi分数。

Radians	Degrees
$\begin{align}\pi\end{align}$	180°
$\begin{align}\frac{\pi}{2}\end{align}$	90°
$\begin{align}\frac{\pi}{3}\end{align}$	60°
$\begin{align}\frac{\pi}{4}\end{align}$	45°
$\begin{align}\frac{\pi}{5}\end{align}$	36°
$\begin{align}\frac{\pi}{6}\end{align}$	30°
$\begin{align}\frac{\pi}{10}\end{align}$	18°
$\begin{align}\frac{\pi}{36}\end{align}$	5°
$\begin{align}\frac{\pi}{180}\end{align}$	1°

T hese base fractions can be used to build radian values. For example, since you know that $\begin{align*}\frac{\pi}{6}=30°,\end{align*}$ you know $\begin{align*}\frac{5\pi}{6} = 30° \times 5 = 150° \text{ and } \frac{11\pi}{6} = 30° \times 11 = 330°.\end{align*}$
::这些基数分数可用于构建弧度值。例如, 由于您知道 = 6= 30 °, 您知道 5 = 6= 30 = 150 °, 11 = 30 = 11= 330 ° 。

While this is helpful for whole number values, real-world numbers don't always work out as nicely. To devise a formula for conversion between degrees and radians , remember that degrees and radians are proportional and that $\begin{align*}2\pi = 360°.\end{align*}$ U se this to create a proportion that can be used to solve for a degree value or a radian value:
::虽然这对整个数字值很有帮助, 但真实世界数字并不总是能很好地发挥作用。要为度和弧度之间的转换设计一个公式, 请记住度和弧度是比例的, 并且是 2360 °。使用这个公式来创建一个比例, 可以用来解析一个度值或弧度值 :

\begin{aligned} \frac{d e g r e e s}{360} = \frac{r a d i a n s}{2 π} \end{aligned}

$\begin{align*}\frac{degrees}{360} = \frac{radians}{2\pi}\end{align*}$
::度360=弧度2

Use the interactive below to practice converting between radians and degrees.
::使用下面的交互效果来练习弧度和度之间的转换。

Discussion Question: - How many different methods can you think of to convert $\begin{align*}\frac{\pi}{3}\end{align*}$ to degrees?
::讨论问题:你能考虑用多少种不同的方法来转换 3 度到 3 度?

Activity 3: Coterminal Angles
::活动3:共同终点角

In addition to angle measures, radians can also be used to describe rotations.
::除角度量外,弧度还可以用来描述旋转。

A counter-clockwise rotation of 30° can also be referred to as a rotation of $\begin{align*}\frac{\pi}{6}\:rads.\end{align*}$ A rotation that runs clockwise is expressed using a negative. A counter-clockwise rotation of 250° can also be referred to as a rotation of $\begin{align*}\frac{25\pi}{18} \: rads.\end{align*}$ It is also possible for a rotation to extend beyond 360°. For example, a rotation of 540 ° would be one and a half full rotations.
::逆时针旋转为 30 °,也可以称为 + 6rads 的旋转。顺时针旋转为负数。反时针旋转为 250 °,也可以称为 25 + 18rads 的旋转为 25 + 18rads。旋转也可延长到 360 °以上。例如,540 °的旋转为 150 个全速旋转。

Example
::示例示例示例示例

Convert -630° to radians
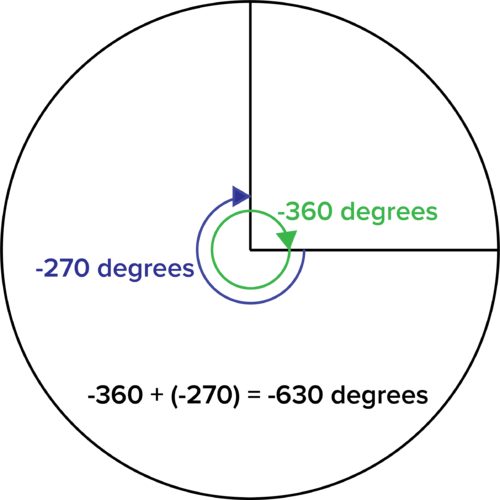
::转换 -630 度为弧度

B egin by visualizing what a -630° rotation would look like.
::开始时可以想象630°的旋转会是什么样子。

You can use all of the same methods presented above to convert any degree measure to radians. In this case, use the proportion stated above.
::您可以使用上述所有相同的方法将任何度量转换为弧度。在此情况下,请使用上述比例。

\begin{aligned} \frac{- 630}{360} = \frac{r}{2 π} \end{aligned}

$\begin{align*}\frac{-630}{360} = \frac{r}{2\pi}\end{align*}$
::- 630360=r2_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

B egin by simplifying the fraction.
::开始简化分数。

\begin{aligned} \frac{- 630}{360} = \frac{- 63 \div 9}{36 \div 9} = \frac{- 7}{4} \end{aligned}

$\begin{align*}\frac{-63 \cancel{0}}{36 \cancel{0}} = \frac{-63\div 9}{36\div9} =\frac{-7}{4}\end{align*}$

This equivalent fraction presents a reduced proportion to work with.
::这一等值分数与相关工作的比例较低。

\begin{aligned} \frac{- 7}{4} = \frac{r}{2 π} \end{aligned}

$\begin{align*}\frac{-7}{4} = \frac{r}{2\pi}\end{align*}$
::- 74=r2_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

C ross multiply and solve the resulting equation to get the answer.
::交叉乘法并解析结果方程式以获得答案。

\begin{aligned} - 7 \cdot 2 π & = 4 \cdot r \\ - 14 π & = 4 r \\ \div 4 & \div 4 \\ \frac{- 14 π}{4} & = r \\ \frac{- 7 π}{2} & = r \end{aligned}

$\begin{align*}-7\cdot 2 \pi &= 4\cdot r\\ -14\pi &=4r\\ \div4\:\:\:\: & \:\div4\\ \frac{-14\pi}{4} &= r\\ \frac{-7\pi}{2} &= r\end{align*}$
::- 7244444 – 144=r-72=r

Answer: -630° converts to $\begin{align*}\frac{-7\pi}{2} \:rads.\end{align*}$
::答复: -630°转换为-72rads。

Different rotations may end up in the same position, known as the terminal side . A ngles that cause two different rotations to land in the same spot are called . Coterminal angles are angles that have the same initial and terminal sides. You can obtain coterminal angles by adding or subtracting 360°, or $\begin{align*}2\pi \end{align*}$ radians.
::不同的旋转最终可能处于同一位置, 称为终端边。导致在同一地点着陆的两种不同旋转的角被称为。 COterminal 角度是初始和终端边的角。您可以通过加或减360°或2+弧度获得共同终点角。

Use the interactive below to extend your knowledge of radians of negative rotations and rotations greater than 360°.
::使用下面的交互效果来扩展您对负旋转和旋转超过360°的弧度的了解。

Extension : Radian Clock
::扩展名: 弧时

Use the interactive below for more practice with radians.
::使用下面的交互效果来用弧度做更多的练习。

Summary

Radians are another way to measure an angle. 360 degrees is equal to 2\pi radians. Convert between degrees and radians using:

$\begin{aligned} \frac{degrees}{360} = \frac{radians}{2 π} \end{aligned}$
$\begin{align*}\frac{\text{degrees}}{360} = \frac{\text{radians}}{2\pi}\end{align*}$
::弧度是测量角度的另一种方式。 360度等于 2\ pi 弧度。以: 度360=radians2} 转换度与弧度之间。

Radians can also be used to describe rotations.
::Radian 也可以用来描述旋转。

Coterminal angles are angles that cause two different rotations to land in the same spot.
::煤矿角是导致在同一地点降落的两种不同旋转角。

Section outline

General

弧度

Introduction: Discovering Radians ::导言:发现雷达

Activity 1: Introduction to Radians ::活动1:瑞迪亚人介绍

Activity 2: Converting Between Radians and Degrees ::活动2:辐射和度之间的转换

Activity 3: Coterminal Angles ::活动3:共同终点角

Extension : Radian Clock ::扩展名: 弧时

Wrap-Up: Questions ::总结:问题

Introduction: Discovering Radians
::导言:发现雷达

Activity 1: Introduction to Radians
::活动1:瑞迪亚人介绍

Activity 2: Converting Between Radians and Degrees
::活动2:辐射和度之间的转换

Activity 3: Coterminal Angles
::活动3:共同终点角

Extension : Radian Clock
::扩展名: 弧时

Wrap-Up: Questions
::总结:问题