7.5 三角函数-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节三角三角函数

  折叠 展开

  三角三角函数

  播放段落

  Lesson Objectives
  ::经验教训目标

  播放段落
  • Graph  functions, showing period, midline, and .
    ::图表函数,显示期间、中线和.。
  播放段落
  • For a function that models a sine or cosine relationship between two quantities, interpret key features of graphs and tables in terms of the quantities .
    ::用于模拟两个数量之间正弦或正弦关系的函数,根据数量解释图表和表格的关键特征。

  ---

  播放段落

  Introduction: Modeling the  Universe
  ::导言:宇宙建模

  播放段落

  Throughout history, many mathematical breakthroughs have come from attempting to describe the way the universe works. M ath is used to describe gravity, planetary motion, sound, light, and so much more. Begin with an astronomical example where the need for a trigonometric function arises.
  ::在整个历史中,许多数学突破都来自试图描述宇宙运作方式。数学用来描述引力、行星运动、声音、光等。首先从一个需要三角函数的天文学例子开始。

  播放段落

  As Earth orbits around the Sun, its distance to the Sun fluctuates due to the Earth's elliptical orbit. The closest point to the Sun is called the perihelion and occurs around January 4th when the Earth is approximately 91,000,000 miles from the sun. The farthest point to the Sun is called the aphelion and occurs around July 5th when the Earth is approximately 95,000,000 miles from the sun. On average, the Earth is approximately 93,000,000 miles from the Sun. T he interactive below displays the  function of Earth's distance from the Sun as its angle of orbit changes.
  ::由于地球环绕太阳的轨道,它与太阳的距离会因地球的椭圆轨道而波动,与太阳的距离最接近的点称为近地点,在地球距太阳约91,000,000英里的1月4日左右发生。太阳的最远点称为远地点,在7月5日左右发生,地球距太阳约95,000,000英里。平均而言,地球距太阳约93,000,000英里。以下互动点显示地球距离太阳的功能是轨道变化的角。

  播放段落

  Discussion Question: What other real-world scenarios can you think of that take on  a similar shape when graphed?
  ::讨论问题:在图表绘制时,你还能想到其他什么现实世界情景?

  ---

  播放段落

  Activity 1: Sine Functions
  ::活动1: Sine 函数

  播放段落

  To model the scenario above, you will need a better understanding of the sine (or sinusoidal) function.
  ::要模拟上述情景,您需要更好地了解正弦(或正弦(或正弦))功能。

  播放段落

  You could use a graph like the unit circle above to  describe this relationship , but  a circle isn't a function. Sine cannot be expressed as a function of cosine. However, sine can be expressed as a function of the angle of rotation . Recall that the y-coordinate of the points along the circle represents the sine of the angle.  Use the interactive below to create the graph of a sine function. 
  ::您可以使用像上面的单位圆圆这样的图形来描述此关系, 但圆不是函数。 Sine 不能以正弦函数表示。 但是, 正弦可以以旋转角度的函数表示。 回顾圆周围点的Y坐标代表角度的正弦值。 使用下面的交互作用来创建正弦函数的图形 。

  播放段落

  Discussion Question: What are the maximum and the minimum values of the function $\begin{array}{r}y=\sin x?\end{array}$   When do they occur?
  ::讨论问题:函数y=sinx的最高值和最低值是多少?这些是何时发生的?

  ---

  播放段落

  Activity 2: Properties of Sine Functions
  ::活动2: Sine 函数的属性

  播放段落

  To map out sine as a function of the angle, observe how the height of the circle changes as the angle increases.
  ::绘制正弦作为角的函数,观察角增加时圆高度的变化。

  播放段落

  Recall that for the unit circle, the coordinates are $\begin{array}{r}(\cos \theta ,\sin \theta ),\end{array}$ where $\begin{array}{r}\theta \end{array}$ is the central angle. The g raph   $\begin{array}{r}y=\sin x\end{array}$  is determined  by re writing the coordinates as $\begin{array}{r}(x,\sin x),\end{array}$ where $\begin{array}{r}x\end{array}$ is the central angle, shown below in radians. 
  ::回想单位圆时,坐标是(cos,sin),坐标是为中心角。图y=sinx通过将坐标重写为(x,sinx)而确定,x是中心角,以下以弧度显示。

  

  播放段落

  Notice that the curve ranges from 1 to -1. The maximum value is 1 at $\begin{array}{r}x=\frac{\pi }{2}\end{array}$ . The minimum value is -1 at $\begin{array}{r}x=\frac{3\pi }{2}\end{array}$ . 
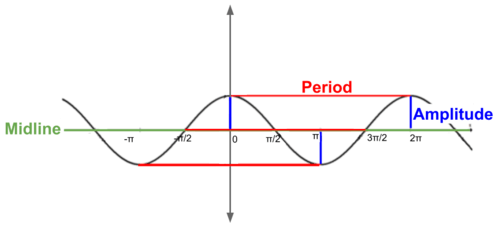
  ::注意曲线介于 1 到 - 1 之间。 最大值为 1 在 x\\ 2 。 最小值为 - 1 在 x= 3 2 。

  播放段落

  The image below identifies the features of a sine function.
  ::以下图像确定了正弦函数的特征 。

  

  播放段落
  • Midline is is the horizontal line that represents the center of a periodic function .
    ::中线是代表周期函数中心的水平线。
  播放段落
  • 播放段落

    is distance between the maximum (or minimum) and the midline.
    ::是最大(或最小)和中线之间的距离。

    
    ::是最大(或最小)和中线之间的距离。
  播放段落
  • 播放段落

    Period is the length of one complete cycle of a periodic function, typically measured as the distance between two maximums (or minimums).
    ::周期是周期函数的一个完整周期的长度,通常以两个最大(或最小)之间的距离衡量。

    
    ::周期是周期函数的一个完整周期的长度,通常以两个最大(或最小)之间的距离衡量。

  播放段落

  Use this information to answer the following questions:
  ::使用此信息回答下列问题:

  播放段落

  Discussion Questions:
  ::讨论问题:

  播放段落
  1. Given the function  $\begin{array}{r}f(x)=\sin (x),\end{array}$ state the y-intercept.
     ::根据函数 f( x) =sin {( x) , 请说明 y 接口 。
  播放段落
  2. Given the function  $\begin{array}{r}f(x)=\sin (x),\end{array}$  state the x-intercept(s).
     ::给定函数 f( x) =sin( x) , 请说明 x 界面 。

  播放段落

  Now that we have a better understanding of sine functions let's return to the example from the introduction.
  ::现在我们对不可缺的功能有了更好的理解,让我们回到引言中的例子。

  ---

  播放段落

  Activity 3: Cosine Functions
  ::活动3: " 附带职能 "

  播放段落

  To find the graph of a cosine function, take the same approach as the sine function with the exception that cosine is the x-value of each point along the unit circle. 
  ::要查找余弦函数的图形,请与正弦函数采取相同的做法,但余弦是单位圆周围每个点的X值。

  播放段落

  The wave of a cosine function begins at 1 because $\begin{array}{r}\cos (0)=1.\end{array}$ The x-value of the unit circle is 1 when the angle is 0. From there, the cosine will decrease until -1 before returning to 1. Use the interactive below to graph the cosine function.
  ::余弦函数的波从 1 开始, 因为 cos( 0) =1. 单位圆的 x 值为 1 , 角度为 0 。 从此, 余弦将下降到 - 1 , 然后再返回到 1 。 使用下面的交互作用来图形余弦函数 。

  播放段落

  Since the sine and cosine functions both represent points on a circle centered about the origin, they both take on the same shape when graphed. The only difference in the graphs of the functions is that they start in different places. Based on these similarities, It should come as no surprise that the cosine function has the same midline, amplitude, and period as the sine function.
  ::由于正弦函数和余弦函数都代表以原为中心圆圈上的点, 两者在图形绘制时都以相同形状出现。 函数图形中唯一的不同之处是它们从不同的地方开始。 基于这些相似之处, 余弦函数具有与正弦函数相同的中线、 振幅和时段并不奇怪 。

  

  播放段落

  You can explore the cosine function further below.
  ::您可以在下面进一步探索余弦函数。

  Summary

  播放段落 The graphs of sine and cosine both take on the same shape. They have the same midline, amplitude and period. The only difference is where they begin. ::正弦和余弦的图形都以相同的形状出现。 它们具有相同的中线、 振幅和时段。 唯一的区别是它们的起点 。 播放段落 The wave of a sine graph starts at (0,0). ::正弦图的波开始于 0,0 。 播放段落 The wave of a cosine graph starts at (0,1). ::余弦图的波起于 0,1 。

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题

  播放段落

  This video further demonstrates the relationship between the graph of a sine function and the unit circle. 
  ::此视频进一步展示正弦函数图与单位圆之间的关系。