章节大纲

  • 常规

    全部折叠 展开全部

  • 通过图表绘制的平方解决系统

    Changing the Game
    ::更改游戏

    Over the past 20 to 30 years, all sports have been undergoing major changes based on analytics. Analytics is the science looking for meaningful patterns in data and statistics. Sports teams have been hiring analysts to help them determine how to build the best team. When making this decision, analysts consider every performance statistic, including salary. The goal is to find the players who will have the best impact on the game within the salary constraints. One of the most famous examples of this comes from the Oakland Athletics, a baseball team that used the “Moneyball” approach to construct their team. The Athletics had very little money so they relied on analytics to find the best players that they could afford. Their strategy worked, and the won three division titles in four years.
    ::在过去20至30年中,所有体育都经历了基于分析的重大变化。分析是科学寻求有意义的数据和统计模式。体育团队一直在聘请分析师,帮助他们决定如何建立最佳团队。在做出这一决定时,分析师会考虑包括工资在内的每一项业绩统计。目标是找到在工资限制范围内对游戏产生最大影响的球员。其中最有名的例子之一是奥克兰Athletics,这是一个棒球队,使用“货币球”方法构建自己的团队。Athletics几乎没有钱,因此他们依靠分析师找到他们能买得起的最佳球员。他们的策略奏效了,四年后赢得了三个分队的称号。

    Another sport which has been heavily impacted by analytics is basketball. In 1979, the NBA introduced the 3-point shot which dramatically affected the strategies teams would take to win games. The teams which were able quickly to test and develop strategies on how to use the 3-point shot had an advantage over their other teams. In the modern NBA,  teams are taking more threes and fewer twos. In this section you  will perform an analysis to answer the question, “Is it better to take 2-pointers or 3-pointers in a basketball game?”
    ::另一个受到分析学严重影响的体育运动是篮球。1979年,NBA引入了三点射击,这极大地影响了战略队赢得比赛的机会。能够快速测试和制定如何使用三点射击战略的球队比其他球队有优势。在现代NBA中,三点和二点的球队比其他球队多。在本节中,你将进行分析回答问题:“在篮球比赛中选二点还是三点的球队更好?”

     

    Changing the Game Continued
    ::更改游戏继续游戏

    To perform  the analysis, you will  follow the same steps that you  did in the previous section.
    ::为了进行分析,你将采取与上一节相同的步骤。

    Identify the Problem or Question
    ::查明问题或问题

    The question is “Is it better to take 2-pointers or 3-pointers in a basketball game?”
    ::问题是“在篮球比赛中选二分还是三分更好吗?”

    Gather Data and Research
    ::收集数据和研究

    Since the introduction of the 3-point shot in 1979, accuracy has increased dramatically from as low as 23.8% to as high as 36.7%. In 2014, NBA teams averaged approximately 1.05 points per 2 point shot and 1.08 points per 3 point shot. A player shooting from 2 point range is more likely to be fouled: in 2014 the NBA teams averaged 12.6 points per game from 2 point shots and 1.07 points per game from 3 point shots. From this data,  you can write the following equations using  x  to represent the number of shots taken and y to represent the number of points scored:
    ::自1979年引入三点射击以来,精确度从23.8%的低点提高到36.7%的峰值。2014年,NBA小组平均每2点射击1.05点,每3点射击1.08点。从2点射程射击的球员更可能犯规:2014年,NBA小组平均每场比赛12.6点,从2点射击,从3点射击每场比赛1.07点。根据这些数据,您可以用x表示射击次数,y表示得分数。

    Points from 2-point shots can be represented by the equation y = 1.05 x + 12.6 . Points from 3-point shots can be represented by the equation y = 1.08 x + 1.07.
    ::2点射击的点可以用公式y=1.05x+12.6表示。3点射击的点可以用公式y=1.08x+1.07表示。

    Analyze the Data
    ::分析数据

    Use the interactive below to graph the system of equations and find the solution.
    ::使用下面的交互效果来绘制方程式系统图,并找到解决办法。

     

     

    Discussion Questions
    ::讨论问题 讨论问题

    1. With a classmate discuss if this data conclusively answer whether a player should take a 2-point shot or a 3-point shot? Should be considered in determining which whether it is better? Do you agree with your classmate? Why or why not?
      ::和同学讨论这些数据是否决定性地回答了玩家是否应该用两点射击还是三点射击的问题?在确定哪个更好时应该考虑吗?你同意你的同学吗?为什么或为什么不行?
    2. Now, discuss if this data this accurate for every individual NBA team? Do you agree with your classmate? Why or why not?
      ::现在,讨论这个数据是否准确 每一个NBA团队?你同意你的同学吗?为什么或为什么不行?
    3. When should a team encourage players to shoot 3-point shots over 2-point shots or vice versa?
      ::球队何时应该鼓励球员在两点射击中三点射击? 还是反之亦然?

       

    Take Action
    ::采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动 采取行动采取行动 采取行动采取行动 采取行动采取行动采取行动 采取行动采取行动采取行动采取行动采取行动采取行动 采取行动采取行动采取行动采取行动采取行动采取行动 采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动采取行动

    If an NBA team takes approximately 384 2-pointers and 384 3-pointers, they will generate the same number of points. The inclusion of free throws adds to the value of a 2-pointer. Because of this, analytics say that the best shots are either close to the basket or 3-point shots. These shot locations have the highest points per shot average.
    ::如果NBA小组选用了大约384个2点和384个3点,它们将产生相同数目的点数。 包括免费投球会增加2点的价值。 因此,分析认为最好的投球要么接近篮子,要么3点。 这些射击地点是每个射击平均最高点。

     

    Supply and Demand
    ::供应和需求

    Another type of analyst who uses systems of equations is an economic analyst. An economic analyst is hired by governments and businesses to help understand how policy changes and consumer trends will affect how people spend money. One way in which they do this using systems of equations is with the supply and demand chart. This chart shows how quantity and price affect supply and demand.
    ::另一种使用方程式系统的分析师是一位经济分析师。 政府和企业聘请了一位经济分析师帮助理解政策变化和消费者趋势将如何影响人们的消费。 他们使用方程式系统的方法之一是用供求图表。 该图表显示了数量和价格如何影响供需。

    lesson content
    Supply and Demand

    Imagine that you own a phone store where you sell the famous phone, the piPhone. If there are only a small number of piPhones made they will need to be sold at a high price to make maximum profit.  However, if you make too many, you will have to lower the price to sell them all. As a business, you must find the equilibrium point where supply meets demand. The equilibrium point represents the maximum price at which you can sell all of the goods that you have/make. You  want to find the equilibrium point for your piPhone.
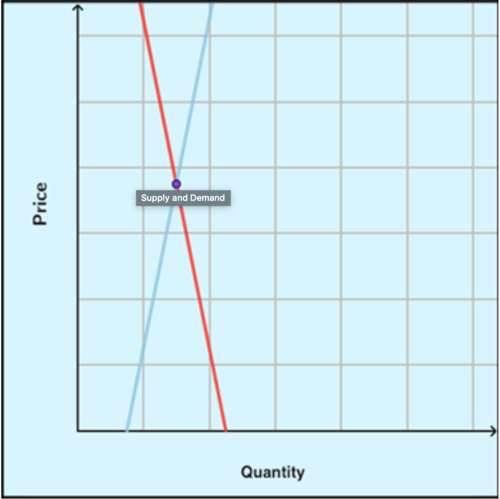
    ::想象一下你拥有一家电话商店,在那里你出售著名的电话,即piPhone。如果只有少量的piPhone制作的,它们需要以高价出售才能获得最大利润。然而,如果数量过大,你必须降低价格才能将其全部出售。作为一个企业,你必须找到供货满足需求的平衡点。平衡点代表你能够出售所有货物的最高价格。你想找到PiPhone的平衡点。

    The interactive below shows the supply and demand for the piPhone, approximated using a linear equation .
    ::下文以线性方程粗略显示PiPhone的供求情况。

    Examine the interactive to analyze how the market can affect the equilibrium point.
    ::检查互动关系,分析市场如何影响平衡点。

     

     

    To check whether or not a point is a solution to a system of equations  you can substitute the x − coordinate  and y − coordinate  into the equation just as  you did in the previous chapter. If it makes both equations true, then it is the solution to the system of equations. The system of equations in the interactive appears to intersect at the point (12.5, 500). C heck this point by substituting it into both equations.
    ::要检查一个点是否是一个方程式系统的解决办法, 您可以和前一章一样, 将 x- 坐标和 y- 坐标替换为方程式。 如果它使两个方程式都是真实的, 那么它就是方程式系统的解决方案。 互动中的方程式系统在点( 12. 5, 500) 似乎是交叉的。 选中此点, 将其替换为两个方程式 。

    y = 40 x ( 500 ) = 40 ( 12.5 ) 500 = 500 ✓


    ::y=40x( 500)=40( 12.5)500=500__

    y = − 40 x + 1000 ( 500 ) = − 40 ( 12.5 ) + 1000 500 = − 500 + 1000 500 = 500 ✓


    ::y40x+100000(500) 40(12.5)+100500_500+100500=500__

    Since both equations are true,  you know that the point (12.5, 500) is the solution to the system of equations.
    ::由于这两个方程式都是真实的,你知道点(12.5,500)是方程式系统的解决办法。

     

     

     

    Number of Solutions
    ::解决方案数目

    I s it possible that two lines cross more than once or do not cross at all?
    ::两条线可能不止跨越一次还是根本不跨越?

    Use the interactive below to determine if this is possible.
    ::使用下面的交互式文字来确定是否可能这样做。

     

     

     

     

    Discussion Questions
    ::讨论问题 讨论问题

    1. What kind of lines do not intersect?
      ::什么样的线条不交叉 ?
    2. What do you know about the slopes and y-intercepts of parallel lines?
      ::你对平行线的斜坡和 Y 探测了解多少?
    3. Discuss with a classmate what kind of lines intersect more than once?
      ::和同学讨论 什么样的直线交错不止一次?
    4. Now, discuss what you know about the slopes and y-intercepts of overlapping lines.
      ::现在,讨论你所了解的 有关斜坡和Y的交叉点 重叠线。
      Summary
    • The solution on the graph of a system of equations is the point where the two lines intersect.
      ::方程系统图上的解决方案是两条线相交的点。
    • Check that a point is the solution to a system of equations by substituting it into both equations.
      ::检查一个点是方程系统的解决办法, 将其替换成两个方程 。