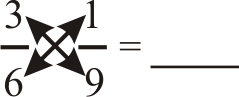7.3两个分数的乘积

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节两个分数的乘积

  折叠 展开

  两个分数的乘积

  

  [Figure 1]

  播放段落

  Simon has  $\begin{array}{r}\frac{3}{4}\end{array}$  of a pie left over from last night's dinner. He wants to take half of the remaining pie to his friend's house. How much pie is Simon taking with him? 
  ::西蒙想把剩下的一半派带去他朋友家 西蒙要和他一起吃多少馅饼?

  播放段落

  In this concept, you will learn how to multiply two fractions.
  ::在这个概念中,你会学会如何乘以两个分数。

  播放段落

  Multiplying Two Fractions
  ::乘法两个分数

  播放段落

  Multiplying fractions can be a little tricky to understand. When adding fractions, you are finding the  sum . When you subtracted fractions, you are finding the  difference . When  multiplying  a fraction by a whole number, you are finding the sum of a repeated fraction or a repeated group.
  ::乘法分数可能有点难以理解。在添加分数时,您正在找到总和。在减去分数时,您正在找到差数。在将一个分数乘以整数时,您正在找到一个重复分数或重复组数的和。

  播放段落

  When you multiply two fractions, it means that you are looking for a part of a part. Here is a multiplication problem with two fractions. 
  ::当乘以两个分数时,这意味着您正在寻找一个部分的一部分。这里有一个乘法问题,有两个分数。

  $$\begin{array}{r}\frac{1}{2}\times \frac{3}{4}=\underset{\_}{}\end{array}$$

  播放段落

  The product is one-half of three-fourths. Here is a diagram.
  ::产品是四分之三的一半。这是一张图表。

  $$\begin{array}{r}\frac{3}{4}\end{array}$$

  

  [Figure 2]

  播放段落

  Three-fourths of the whole is shaded. To find one-half of the three-fourths,  divide  the entire diagram in half.
  ::整体的四分之三是阴影。要找到四分之三的一半,将整张图一分为二。

  

  [Figure 3]

  播放段落

  The diagram is evenly divided into 8 parts. The shaded parts is divided into 6 parts. The gray shaded part represents half of the three-fourths. Therefore,  $\begin{array}{r}\frac{1}{2}\end{array}$  of  $\begin{array}{r}\frac{3}{4}=\frac{3}{8}\end{array}$ .
  ::图表平均分为8个部分,阴影部分分为6个部分,灰色部分占四分之三的一半,因此,3 4 = 3 8中的12个部分。

  播放段落

  You can’t always draw pictures to figure out a problem, so you can multiply fractions using a few simple steps.
  ::您不能总是绘制图片来找出问题, 这样您就可以使用几个简单的步骤来乘以分数 。

  播放段落

  To multiply two fractions, multiply the  numerator  by the numerator and the  denominator  by the denominator. 
  ::要乘以两个分数,将分子乘以分子,分母乘以分母。

   

  $$\begin{array}{r}\frac{a}{b}\times \frac{c}{d}=\frac{a\times c}{b\times d}\end{array}$$

  播放段落

  Here is an example.
  ::举一个例子。

  $$\begin{array}{r}\frac{1}{2}\times \frac{3}{4}=\underset{\_}{}\end{array}$$

  播放段落

  Multiply the first  numerator by the second numerator and multiply the first denominator by the second denominator.
  ::乘以第一个分子,乘以第二个分子,乘以第一个分母,乘以第二个分母。

    

  $$\begin{array}{r}\frac{1}{2}\times \frac{3}{4}=\frac{1\times 3}{2\times 4}=\frac{3}{8}\end{array}$$

  播放段落

  The product is  $\begin{array}{r}\frac{3}{8}\end{array}$ . The answer is the same as the one found earlier.
  ::产品为3,8。答案与先前的相同。

  播放段落

  Let's look at another example.
  ::让我们再举一个例子。

  $$\begin{array}{r}\frac{3}{6}\times \frac{1}{9}=\underset{\_}{}\end{array}$$

  播放段落

  First, multiply the numerator by the numerator and the denominator by the denominator.
  ::首先,将分子乘以分子,分母乘以分母。

  $$\begin{array}{r}\frac{3\times 1}{6\times 9}=\frac{3}{54}\end{array}$$

  播放段落

  Next,  simplify  the fraction  $\begin{array}{r}\frac{3}{54}\end{array}$  by dividing by the   (GCF). The GCF of 3 and 54 is 3. 
  ::其次,简化第354项,除以(GCF),3和54的绿色气候基金为3。

  $$\begin{array}{r}\frac{3÷3}{54÷3}=\frac{1}{18}\end{array}$$

  播放段落

  The product is  $\begin{array}{r}\frac{1}{18}\end{array}$ .
  ::产品是1 18。

  播放段落

  To solve this problem, you multiplied and then simplified. Sometimes, you can simplify before multiplying. Let's look at the problem again.
  ::要解决这个问题, 您需要乘数, 然后简化 。 有时, 您可以在乘数之前简化 。 让我们再看一下问题 。

  $$\begin{array}{r}\frac{3}{6}\times \frac{1}{9}=\underset{\_}{}\end{array}$$

  播放段落

  There are two ways you can simplify this problem before multiplying.
  ::在乘法之前,有两种方法可以简化这个问题。

  播放段落
  1. Simplify any fractions that can be simplified.
     ::简化可以简化的任何分数 。

  播放段落

   Here three-sixths can be simplified to one-half. The new problem would be  $\begin{array}{r}\frac{1}{2}\times \frac{1}{9}=\frac{1}{18}\end{array}$ .
  ::这里的六分之三可以简化为一半。 新的问题将是 1 2 × 1 9 = 1 18 。

  播放段落
  2. Cross simplify the fractions.  
     ::交叉简化分数。

  播放段落

  To  cross-simplify , simplify on the diagonals by using greatest common  factors  to simplify a numerator and an opposite denominator. 
  ::交叉简化,利用最共同的因素简化分子和对立分母,从而简化对角体。

  

  [Figure 4]

  播放段落

  Look at the numbers on the diagonals and simplify any that you can. Now, 1 and 6 can not be simplified, but 3 and 9 have the GCF of 3.
  ::看看对角线上的数字, 并简化任何您可以简化的数字。 现在, 1 和 6 无法简化, 但3 和 9 全球合作框架为 3 。

  $$\begin{array}{rl}3÷3& =1\\ 9÷3& =3\end{array}$$

  播放段落

  Next, substitute the new numbers for the old ones and multiply. 
  ::接下来,用新数字代替旧数字,再乘法。

  $$\begin{array}{r}\frac{1}{6}\times \frac{1}{3}=\frac{1}{18}\end{array}$$

  播放段落

  Notice that you can simplify three different ways, but will always end up with the same answer.
  ::请注意,您可以简化三种不同的方式,但最终总是得到相同的答案。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about Simon and his pie.
  ::早些时候,你得到一个问题 关于西蒙和他的派。

  播放段落

  Simon is taking half of  $\begin{array}{r}\frac{3}{4}\end{array}$  of a pie to his friends house. Multiply one-half times  $\begin{array}{r}\frac{3}{4}\end{array}$  to find the  amount  of pie Simon is taking with him.
  ::西蒙拿了三块四分半的馅饼去朋友家 乘以五乘以三块四

  $$\begin{array}{r}\frac{1}{2}\times \frac{3}{4}=\underset{\_}{}\end{array}$$

  播放段落

  First, multiply the fraction. Find the product of the numerators over the product of the denominators. 
  ::首先,乘以分数。在分母的产物上找到分子的产物。

  $$\begin{array}{r}\frac{1\times 3}{2\times 4}=\frac{3}{8}\end{array}$$

  播放段落

  The fraction is in  simplest form .
  ::分数以最简单的形式出现。

  播放段落

  Simon is taking  $\begin{array}{r}\frac{3}{8}\end{array}$  of a pie with him to his friend's house. 
  ::西蒙带着三十八块馅饼去他朋友家

  播放段落

  Example 2
  ::例2

  播放段落

  Find the product. Answer in simplest form.
  ::找到产品,回答最简单

  $$\begin{array}{r}\frac{3}{7}\times \frac{2}{3}=\underset{\_}{}\end{array}$$

  播放段落

  First, multiply the numerator by the numerator and the denominator by the denominator. 
  ::首先,将分子乘以分子,分母乘以分母。

  $$\begin{array}{r}\frac{3\times 2}{7\times 3}\underset{\to }{\stackrel{\to }{=}}\frac{6}{21}\end{array}$$

  播放段落

  Then, simplify the fraction. Divide 6 and 21 by the GCF of 3.
  ::然后,简化分数。除以6和21,由全球合作框架的3除以6和21。

  $$\begin{array}{r}\frac{6÷3}{21÷3}\underset{\to }{\stackrel{\to }{=}}\frac{2}{7}\end{array}$$

  播放段落

  The product is  $\begin{array}{r}\frac{2}{7}\end{array}$ .
  ::产品为2 7。

  播放段落

  Example 3
  ::例3

  播放段落

  Find the product:  $\begin{array}{r}\frac{4}{5}\times \frac{1}{2}=\underset{\_}{}\end{array}$ . Answer in simplest form.
  ::查找产品: 4 5 × 1 2 = _. 回答最简单。

  播放段落

  First, multiply the numerator by the numerator and the denominator by the denominator.
  ::首先,将分子乘以分子,分母乘以分母。

  $$\begin{array}{r}\frac{4\times 1}{5\times 2}=\frac{4}{10}\end{array}$$

  播放段落

  Then, simplify the fraction. The GCF of 4 and 10 is 2.
  ::然后简化分数,全球合作框架4和10是2。

  $$\begin{array}{r}\frac{4}{10}=\frac{2}{5}\end{array}$$

  播放段落

  The product is  $\begin{array}{r}\frac{2}{5}\end{array}$ .
  ::产品为2 5。

  播放段落

  Example 4
  ::例4

  播放段落

  Find the product:  $\begin{array}{r}\frac{6}{9}\times \frac{1}{3}=\underset{\_}{}\end{array}$ . Answer in simplest form.
  ::查找产品: 6 9x1 3 = _. 回答最简单。

  播放段落

  First, simplify the fraction  $\begin{array}{r}\frac{6}{9}\end{array}$  and rewrite the problem. The GCF of 6 and 9 is 3.
  ::首先,简化第6部分9,重写问题,全球合作框架6和9是3。

  $$\begin{array}{r}\frac{6}{9}=\frac{2}{3}\end{array}$$

   

  $$\begin{array}{r}\frac{2}{3}\times \frac{1}{3}\end{array}$$

  播放段落

  Then, multiply the numerator by the numerator and the denominator by the denominator.
  ::然后,将分子乘以分子,分母乘以分母。

   

  $$\begin{array}{r}\frac{2\times 1}{3\times 3}=\frac{2}{9}\end{array}$$

  播放段落

  The product is  $\begin{array}{r}\frac{2}{9}\end{array}$ .
  ::产品为2 9。

  播放段落

  Example 5
  ::例5

  播放段落

  Find the product:  $\begin{array}{r}\frac{5}{6}\times \frac{2}{3}=\underset{\_}{}\end{array}$ . Answer in simplest form.
  ::查找产品: 5 6 × 2 3 = _. 回答最简单。

  播放段落

  First, cross simplify the fractions. The GCF of 2 and 6 is 2. 
  ::首先,交叉简化分数,全球合作框架2和6是2。

  $$\begin{array}{r}\frac{5}{\cancel{6}}\times \frac{\cancel{2}}{3}=\frac{5}{3}\times \frac{1}{3}\end{array}$$

  播放段落

  Then, multiply the numerator by the numerator and the denominator by the denominator.
  ::然后,将分子乘以分子,分母乘以分母。

   

  $$\begin{array}{r}\frac{5\times 1}{3\times 3}=\frac{5}{9}\end{array}$$

  播放段落

  The product is  $\begin{array}{r}\frac{5}{9}\end{array}$ .
  
  ::产品为5 9。

  播放段落

  Review
  ::回顾

  播放段落

  Find the product. Answer in simplest form.
  ::找到产品,回答最简单

  1. $\begin{array}{r}\frac{1}{6}\times \frac{1}{3}=\underset{\_}{}\end{array}$
  2. $\begin{array}{r}\frac{1}{4}\times \frac{1}{2}=\underset{\_}{}\end{array}$
  3. $\begin{array}{r}\frac{4}{5}\times \frac{1}{3}=\underset{\_}{}\end{array}$
  4. $\begin{array}{r}\frac{6}{7}\times \frac{1}{2}=\underset{\_}{}\end{array}$
  5. $\begin{array}{r}\frac{1}{8}\times \frac{1}{4}=\underset{\_}{}\end{array}$
  6. $\begin{array}{r}\frac{2}{3}\times \frac{1}{4}=\underset{\_}{}\end{array}$
  7. $\begin{array}{r}\frac{1}{5}\times \frac{1}{2}=\underset{\_}{}\end{array}$
  8. $\begin{array}{r}\frac{2}{5}\times \frac{3}{6}=\underset{\_}{}\end{array}$
  9. $\begin{array}{r}\frac{7}{9}\times \frac{2}{3}=\underset{\_}{}\end{array}$
  10. $\begin{array}{r}\frac{8}{9}\times \frac{3}{4}=\underset{\_}{}\end{array}$
  11. $\begin{array}{r}\frac{2}{3}\times \frac{1}{2}=\underset{\_}{}\end{array}$
  12. $\begin{array}{r}\frac{4}{7}\times \frac{2}{14}=\underset{\_}{}\end{array}$
  13. $\begin{array}{r}\frac{6}{7}\times \frac{2}{5}=\underset{\_}{}\end{array}$
  14. $\begin{array}{r}\frac{4}{9}\times \frac{1}{2}=\underset{\_}{}\end{array}$
  15. $\begin{array}{r}\frac{8}{9}\times \frac{2}{5}=\underset{\_}{}\end{array}$
  16. $\begin{array}{r}\frac{3}{8}\times \frac{2}{3}=\underset{\_}{}\end{array}$

  播放段落

  Review (Answers) 
  ::回顾(答复)

  播放段落

  Click   to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源