10.5π
章节大纲
-
Carla has to go to the store and get a tablecloth for the round table in the dining room. In order to get the right size tablecloth, she needs to know the distance from one side of the table to the other side. The 3-foot long yardstick she has can only measure up to the center of the table, or halfway across. How can Carla figure out the distance across the circular table with only the yardstick and then use that information to find out the of the table?
::Carla必须到商店去买一张桌布,用于在餐厅里举行圆桌会。为了得到合适的桌布,她需要知道从桌子一边到另一边的距离。她只有三英尺长的标尺才能测量到桌子中间或中间。Carla怎么能够用仅仅的标尺找到圆桌的距离,然后用这些信息找出桌子的距离?In this concept, you will learn the relationship between diameter and radius and identify pi as the ratio of diameter to circumference in a circle .
::在此概念中,您将学习直径和半径之间的关系,并将 pi 确定为圆形中直径与环绕之比。Circle Relationships
::圆圈关系To work with circles, you need to know the different parts of a circle and how these key parts are measured.
::要与圆圈合作, 您需要知道圆圈的不同部分, 以及如何测量这些关键部分 。You can measure the distance across the center of the circle. This distance is called the diameter of the circle.
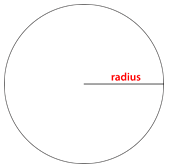
::您可以测量圆圆中心之间的距离。 这个距离被称为圆的直径 。You can measure the distance from the center of the circle to the outer edge . This distance is called the radius .
::您可以测量圆的中心到外缘的距离。 这个距离被称为半径 。Notice that the radius is one-half of the measure of the diameter.
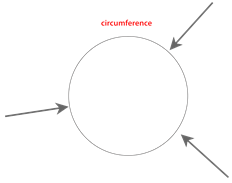
::注意半径是直径的半径半径。You can measure the perimeter of the circle too. This distance is called the circumference of the circle.
::您也可以测量圆圈的周界。 这个距离被称为圆圈的环绕 。Archimedes , a mathematician in ancient Greece, is credited with figuring out the relationship between the diameter and circumference of a circle. Archimedes discovered that if you take the distance across the circle (diameter) and stretch it around the circumference, it would take a little over 3 lengths of the diameter to go around the circumference of the circle.
::古希腊的一个数学家Archimedes在了解圆的直径和环绕之间的关系方面功不可没。 Archimedes发现,如果你在圆圈(直径)的距离上走过圆圈(直径)并绕环绕环绕圈,绕圆圈绕圈需要略高于直径三长的距离。Let’s say that the diameter of this circle is 5 cm, in that case the circumference of the circle is three and a little more times the 5 cm, or a little less than 16 cm.
::假设这个圆的直径是 5 厘米, 圆的环绕是 3 比5 厘米多一点, 或小于 16 厘米。The ratio of the diameter to the circumference is called pi, . The numerical value of pi is a non-terminating decimal, which means it cannot be written precisely as a numeral since the decimal places never end or form a pattern. So, the number 3.14 is used to represent pi and is used for estimating the circumference of a circle.
::直径与环绕的比对称为 pi, 。 pi 的数值值是非终止的小数, 这意味着它不能精确地写成数字, 因为小数点从不结束或形成一个图案。 因此, 数字3. 14 用于代表 pi , 用于估计圆圈的环绕 。Examples
::实例Example 1
::例1Earlier, you were given a problem about Carla and her trouble measuring the diameter of the round table.
::早些时候,你遇到了一个问题 关于卡拉和她的问题 测量圆桌的直径。Carla was still debating how to find the diameter of the round table when her mother walked in the dining room. When Carla explained the problem to her mom, her mom told her if the 3-foot long yardstick measured the distance from the edge of the table to the center point , then that was the radius of the table. Knowing the radius of the table was 3 feet, Carla knew she could use the relationship formula for radius and diameter to figure out the distance from one side of the table to the other.
::Carla还在争论如何找到圆桌的直径,当时她的母亲走进餐厅。当Carla向她的母亲解释这个问题时,她的母亲告诉她,如果用三英尺长的尺度测量从桌子边缘到中间点的距离,那么这就是桌子的半径。知道桌子的半径是3英尺,Carla知道她可以用半径和直径的关系公式来算出从桌子一边到另一边的距离。First, Carla substituted the given measurement in the formula for diameter and radius.
::首先,卡拉替换了直径和半径公式中给定的测量。Next, she multiplied 2 times 3.
::接下来,她乘以2乘以3乘以2乘以3The table’s diameter is 6 feet.
::桌子的直径为6英尺。Carla could use this information to figure out the circumferences of the table by multiplying the diameter and pi (3.14).
::卡拉可以利用这一信息通过直径和pi(3.14)乘以直径和pi(3.14)来查明表格的周长。Example 2
::例2Use the given value for the radius to find the diameter.
::使用半径的给定值查找直径 。If the radius of a circle is 3, what is the diameter?
::如果圆的半径是3,直径是多少?First, note the definition of radius and diameter. The radius is one-half the diameter or the diameter is twice the length of the radius.
::首先,请注意半径和直径的定义。半径为直径的一半,直径是半径的两倍。Next, multiply the radius by 2 to get 6.
::接下来,将半径乘以 2 乘以 6 。The answer is 6.
::答案是6个Example 3
::例3If a circle has a diameter of 14 inches, what is its radius?
::如果圆的直径为14英寸,其半径是多少?First, substitute the given measurement in the formula for diameter and radius.
::首先,替换直径和半径公式中的给定测量。Next, divide both sides by 2.
::其次,将双方除以2。The answer is 7.
::答案是7个Example 4
::例4If a circle has a radius of 11 inches, what is its diameter?
::如果圆的半径为11英寸,其直径是多少?First, substitute the given measurement in the formula for diameter and radius.
::首先,替换直径和半径公式中的给定测量。Next, multiply 2 and 11.
::下一个乘以2和11The answer is 22.
::答案是22。Example 5
::例5If a circle has a diameter of 18 inches, what is its radius?
::如果圆的直径为18英寸,其半径是多少?First, substitute the known values in the equation.
::首先,用方程式中已知的值替代。Next, do the math and divide both sides by 2.
::接下来,进行计算,把两边除以2。The answer is 9.
::答案是9。Review
::回顾Given each radius, determine the diameter.
::给每个半径定位, 确定直径 。-
::r = 4 i n 。 -
::r = 6 i n 。 -
::r = 5 i n 。 -
::r = 12 i n 。 -
::r = 16 f t. -
::r = 28米。 -
::r = 12.5英尺 -
::r=1.25米。
Given each diameter, determine the radius.
::视每个直径,确定半径。-
::d = 12米。 -
::d = 18米。 -
::d = 12.5 i n 。 -
::d = 18.5 f t. -
::d = 9.8 i n 。 -
::d = 1.45米。 -
::d = 1.75 f t. -
::d = 2.5 f t. -
::d = 221.25米。
-