10.18圆柱体积

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节圆柱体积

  折叠 展开

  圆柱体积

  

  [Figure 1]

   

  播放段落

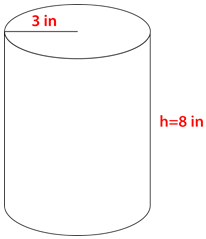
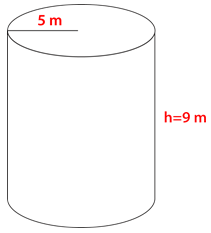
  Ramona prepared a large pot of fruit preserves, but she ran out of canning jars before she had canned all of the preserves. She took two food storage containers out of the cupboard. The cylindrical containers have the  dimensions  below. There isn’t enough of the extra preserve for both containers, so she only needs one of the containers and it needs to be the one with the greatest  .
  ::Ramona准备了一大锅水果储藏,但在她把罐头罐子都罐了之前,她就用完了。 她从橱柜里拿走了两个食品储藏箱。 圆柱体容器的尺寸如下。 两个容器都没有足够的额外储藏箱,所以她只需要一个容器,它需要的是最大的容器。

  

  [Figure 2]

  播放段落

  How can Ramona use these dimensions to figure out which container will hold the most?
  ::蕾蒙娜如何利用这些维度来决定哪个集装箱能容纳最多?

  播放段落

  In this concept, you will learn to use formulas to find the volume of cylinders.
  ::在这个概念中,你会学会使用公式来找到气瓶的体积。

  播放段落

  Finding Volume of Cylinders
  ::查找气瓶数量

  播放段落

  Volume  is the amount of  space  contained within a  . In the case of cylinders, you can think of volume as the capacity, or the amount of a liquid or substance, it can hold.
  ::体积是指一个气瓶内所含空间的数量。在气瓶的情况下,你可以将体积视为容量,或液体或物质的数量,它可以保持。

  播放段落

  Unlike prisms, unit cubes do not fit nicely into a  cylinder .
  ::与棱晶不同,单体立方体不适合装在圆柱体中。

  

  [Figure 3]

  播放段落

  So, to calculate the volume of a cylinder accurately, you need to use a formula instead of unit cubes.
  ::所以,要精确计算圆柱体的体积, 您需要使用公式而不是单位立方体。

  播放段落

  To calculate the volume of a cylinder, start by calculating the  area  of the circular base. That will give you a  measure  for the number of unit cubes that can fit across the bottom of the cylinder. The  height  of the cylinder will show how high cubes can be stacked inside the cylinder.
  ::要计算圆柱体的体积, 请首先计算圆柱体的面积。 这将为您提供一个测量可划过圆柱体底部的单位立方体数的尺度。 圆柱体的高度将显示圆柱体内如何堆叠高立方体 。

  播放段落

  Here is the formula for finding the volume of a cylinder.
  ::这是找到圆柱体体积的公式。

  $$\begin{array}{r}V=\pi r^{2}h\end{array}$$

  播放段落

  Let’s apply this formula.
  ::让我们应用这个公式。

  

  [Figure 4]

  播放段落

  
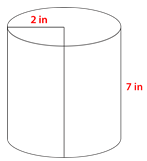
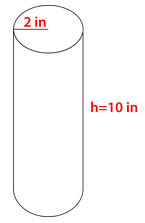
  The  radius  of the circular base is 2 inches. The height of the cylinder is 7 inches. If you take both of these given measures and substitute them into the formula, you can solve for the volume of the cylinder.
  ::圆形基点的半径为 2 英寸。圆形基点的高度为 7 英寸。如果您采取上述两种措施并将其替换为公式,您可以解析圆形柱体的体积。

  $$\begin{array}{r}\begin{array}{rcl}V& =& \pi r^{2}h\\ V& =& (3.14)(2^2)(7)\\ V& =& (3.14)(4)(7)\\ V& =& (3.14)(28)\\ V& =& 87.92i{n}^3\end{array}\end{array}$$

  播放段落

  The volume of the cylinder is  $\begin{array}{r}87.92i{n}^3\end{array}$ .
  ::气瓶的体积为87.92 i n 3。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1 
  ::例1

  播放段落

  Earlier, you were given a problem about Ramona and her extra fruit preserve.
  ::早些时候,你得到一个问题 关于蕾蒙娜 和她额外的水果保护。

  播放段落

  Ramona has two food storage containers, but isn’t sure which will hold the most. How can Raymond use these dimensions to figure out which will hold the most?
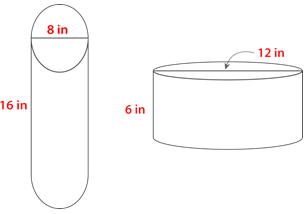
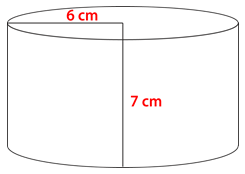
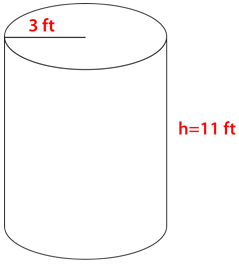
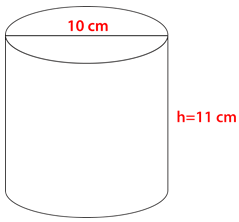
  ::雷蒙娜有两个食品储藏箱,但不确定哪个容器能控制得最多。 雷蒙德如何利用这些维度来决定哪个容器能控制得最多?

  

  [Figure 5]

  播放段落

  Start with the container on the left.
  ::从左边的集装箱开始

  播放段落

  First, note that the  diameter  is twice the radius, so divide the diameter by 2 to get the radius.
  ::首先,请注意直径是半径的两倍, 所以直径除以 2 以获得半径 。

  $\begin{array}{r}8÷2=4\end{array}$

  播放段落

  Radius is 4.
  ::半径是4。

  播放段落

  Next, substitute the given information into the formula then solve.
  ::下一步,将给定信息替换到公式中,然后解析 。

  $$\begin{array}{r}\begin{array}{rcl}V& =& \pi r^{2}h\\ V& =& \pi (4{)}^2(16)\\ V& =& \pi (16)(16)\\ V& =& 256\pi \\ V& =& 803.84in{.}^3\end{array}\end{array}$$

  播放段落

  The first container holds 803.84 cubic inches.
  ::第一个集装箱有803.84立方英寸。

  播放段落

  Next, consider the other container.
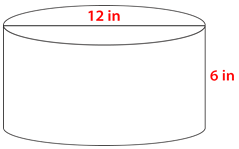
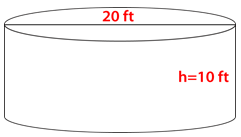
  ::接下来,考虑另一个容器。

  播放段落

  First, note that the diameter is twice the radius, so divide the diameter by 2 to get the radius.
  ::首先,请注意直径是半径的两倍, 所以直径除以 2 以获得半径 。

  $\begin{array}{r}12÷2=6\end{array}$

  播放段落

  Radius is 6.
  ::半径是6

  播放段落

  Next, substitute the given information into the formula then solve.
  ::下一步,将给定信息替换到公式中,然后解析 。

  $$\begin{array}{r}\begin{array}{rcl}V& =& \pi r^{2}h\\ V& =& \pi (6{)}^2(6)\\ V& =& \pi (36)(6)\\ V& =& 216\pi \\ V& =& 678.24in{.}^3\end{array}\end{array}$$

  播放段落

  The second container holds 678.24 cubic inches.
  ::第二个集装箱内有678.24立方英寸。

  播放段落

  The container on the left has the greatest volume.
  ::左边的集装箱体积最大。

  播放段落

  Example 2
  ::例2

  播放段落

  Use the formula for finding the volume of a cylinder to answer the following question.
  ::使用找到圆柱体体积的公式回答下列问题。

  播放段落

  A water tank has a radius of 50 feet and a height of 400 feet. How many cubic feet of water will the tank hold when it is full?
  ::水箱半径为50英尺,高度为400英尺。 水箱满载时将保持多少立方英尺的水?

  播放段落

  First, substitute the given information into the formula and solve. 
  ::首先,将给定信息替换为公式和解析。

  $$\begin{array}{r}\begin{array}{rcl}V& =& \pi r^{2}h\\ V& =& \pi ({50}^2)(400)\\ V& =& \pi (2,500)(400)\\ V& =& 1,000,000\pi \\ V& =& 3,140,000in{.}^3\end{array}\end{array}$$

  播放段落

  The water tank will hold more than 3  million  cubic feet of water!
  ::水箱将容纳300多万立方英尺的水!

  播放段落

  Example 3
  ::例3

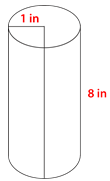
  播放段落

  Find the volume of the cylinder.
  ::找到气瓶的体积。

  

  [Figure 6]

  播放段落

  First, substitute the given information into the formula then solve. 
  ::首先, 将给定信息替换为公式, 然后解析 。

  $$\begin{array}{r}\begin{array}{rcl}V& =& \pi r^{2}h\\ V& =& \pi (1^2)(8)\\ V& =& \pi (1)(8)\\ V& =& 8\pi \\ V& =& 25.12in{.}^3\end{array}\end{array}$$

  The answer is 25.12 cubic inches.

  播放段落

  Example 4
  ::例4

  播放段落

  Find the volume of the cylinder.
  ::找到气瓶的体积。

  播放段落

  $\begin{array}{r}d=10ft,h=12ft\end{array}$
  ::d = 10 f t, h = 12 f t = 10 f t, h = 12 f t

  播放段落

  First, note that the diameter is twice the radius, so divide the diameter by 2 to get the radius.
  ::首先,请注意直径是半径的两倍, 所以直径除以 2 以获得半径 。

  $\begin{array}{r}10÷2=5\end{array}$

  播放段落

  Radius is 5.
  ::半径是5

  播放段落

  Next, substitute the given information into the formula then solve.
  ::下一步,将给定信息替换到公式中,然后解析 。

  $$\begin{array}{r}\begin{array}{rcl}V& =& \pi r^{2}h\\ V& =& \pi (5{)}^2(12)\\ V& =& \pi (25)(12)\\ V& =& 300\pi \\ V& =& 942ft{.}^3\end{array}\end{array}$$

  播放段落

  The answer is 942 cubic feet.
  ::答案是942立方英尺

  播放段落

  Example 5
  ::例5

  播放段落

  Find the volume of the cylinder.
  ::找到气瓶的体积。

  播放段落

  $\begin{array}{r}r=6in,h=10in\end{array}$
  ::r = 6 i n, h = 10 i n

  播放段落

  First, substitute the given information into the formula then solve.
  ::首先, 将给定信息替换为公式, 然后解析 。

  $$\begin{array}{r}\begin{array}{rcl}V& =& \pi r^{2}h\\ V& =& \pi (6{)}^2(10)\\ V& =& \pi (36)(10)\\ V& =& 360\pi \\ V& =& 1130.4in{.}^3\end{array}\end{array}$$

  播放段落

  The answer is 1130.4 cubic inches.
  ::答案是1130.4立方英寸

  播放段落

  Review
  ::回顾

  播放段落

  Find the volume of each of the following cylinders. Use the value approximated value 3.14 for the number  $\begin{array}{r}\pi .\end{array}$
  ::查找以下每个气瓶的体积。使用数字 的大约值3.14。

  播放段落
  1. $\begin{array}{r}r=5in,h=8in\end{array}$  
     ::r = 5 i n, h = 8 i n
  播放段落
  2. $\begin{array}{r}r=4in,h=7in\end{array}$  
     ::r = 4 i n, h = 7 i n
  播放段落
  3. $\begin{array}{r}r=3ft,h=5ft\end{array}$  
     ::r = 3 f t, h = 5 f t
  播放段落
  4. $\begin{array}{r}r=3ft,h=8ft\end{array}$  
     ::r = 3 f t, h = 8 f t
  播放段落
  5. $\begin{array}{r}r=4cm,h=9cm\end{array}$  
     ::r = 4厘米,h = 9厘米

  播放段落
  6. 

     [Figure 7]
     
     ::[图7]
  播放段落
  7. 

     [Figure 8]
     
     ::[表8]
  播放段落
  8. 

     [Figure 9]
     
     ::[图9]
  播放段落
  9. 

     [Figure 10]
     
     ::[图10]
  播放段落
  10. 

      [Figure 11]
      
      ::[表11]
  播放段落
  11. 

      [Figure 12]
      
      ::[图12]
  播放段落
  12. 

      [Figure 13]
      
      ::[图13]
  播放段落
  13. 

      [Figure 14]
      
      ::[表14]
  播放段落
  14. 

      [Figure 15]
      
      ::[图15]
  播放段落
  15. 

      [Figure 16]
      
      ::[图16]