计算机科学基础
计算的定义
在本课程中,我们试图聚焦于计算原理(大思想),而不是计算机技术,后者只是这些原理的工具和应用。计算是由一组原理或思想定义的,这些原理支撑着基于它们创建的各种技术。技术可能复杂且不断发展,但原理保持不变。在课程的后半部分,我们将学习各种技术,以展示计算的力量以及原理是如何应用的。
除了计算原理和技术,还有计算实践——即专业人员为推动计算发展所做的工作。
右侧的图表说明了计算原理与计算实践之间的区别。原理支撑着技术和实践。消费者通过为他们构建的应用程序,在各种任务中利用计算的力量。我们认为每个人都需要了解计算原理,因为这些原理具有广泛的适用性。作为计算领域的专业人士,我们需要了解计算的两个端点以及中间的一切——实践(使计算有用且有效的活动和技能)。
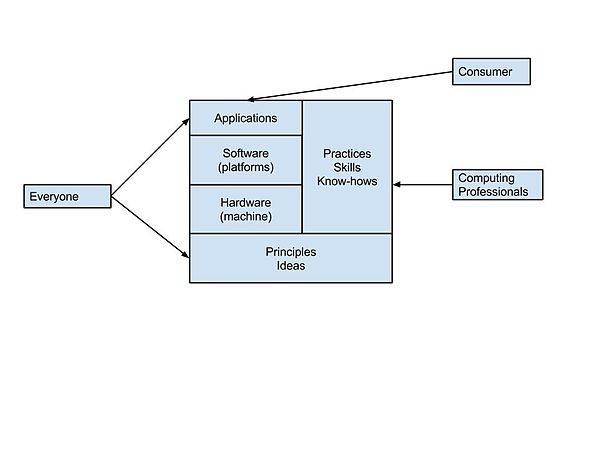
此图表展示了计算原理与计算实践之间的区别。
我们将在全书中交替使用“计算”和“计算过程”这两个术语。
计算原理
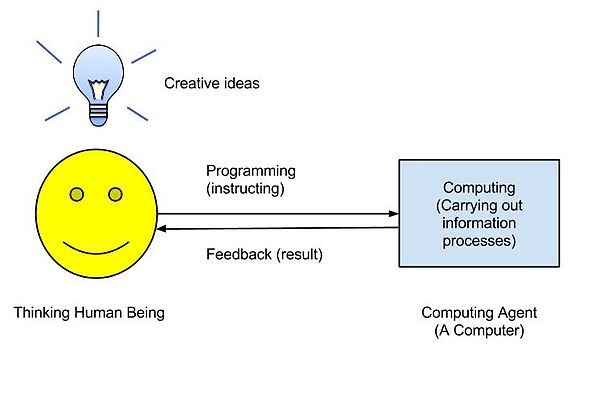
计算本质上是关于信息处理的。计算的一个重要理念是,信息处理可以通过符号操作纯粹机械地完成。进行计算的主体,无论是思考的人类还是机器(计算机),都不重要。在本书的后部分,我们将看到这一点对于所有现代计算机都是成立的——数字计算机根据指令盲目地操作两种符号(零和一)。
类比
以下来自《作为计算的思维》一书的类比[1]阐述了这个理念。假设我们有如下符号表:
| a | b | c | d | e | f | g | h | i | j | |
|---|---|---|---|---|---|---|---|---|---|---|
| a | aa | ab | ac | ad | ae | af | ag | ah | ai | aj |
| b | ab | ac | ad | ae | af | ag | ah | ai | aj | ba |
| c | ac | ad | ae | af | ag | ah | ai | aj | ba | bb |
| d | ad | ae | af | ag | ah | ai | aj | ba | bb | bc |
| e | ae | af | ag | ah | ai | aj | ba | bb | bc | bd |
| f | af | ag | ah | ai | aj | ba | bb | bc | bd | be |
| g | ag | ah | ai | aj | ba | bb | bc | bd | be | bf |
| h | ah | ai | aj | ba | bb | bc | bd | be | bf | bg |
| i | ai | aj | ba | bb | bc | bd | be | bf | bg | bh |
| j | aj | ba | bb | bc | bd | be | bf | bg | bh | bi |
这些符号可以是任何一组符号,我们为了简化选择了英文字母。我们可以定义一个过程P,该过程接受两个符号('a'到'j')作为输入,并输出同一组符号中的两个符号。内部,过程使用第一个输入符号找到以相同符号开头的行,然后使用第二个输入符号找到顶部有相同符号的列,最后报告/返回交点处的符号。可以想象,这样的表格查找过程可以由一个简单的代理(例如一个设备或机器)纯粹机械地(盲目地)完成。当然,人类也可以做到这一点,但这种符号操作不需要人类的智慧。从这个思维实验中可以得出两个结论:
- 符号操作可以通过机械方式完成。
- 执行操作的机器不需要知道符号的意义,也不需要知道操作的目的。
这个过程在我们知道如何解释符号时是有意义的。例如,如果符号“a”到“j”分别表示数量0到9,那么这个过程就执行了单个位数的十进制加法。例如,p(d, f) = p(3, 5) = ai = 08,这是3+5的正确结果。下面的表格本质上与前一个表格相同,只是它使用了对人类有意义的符号。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 |
| 1 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 |
| 2 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 |
| 3 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 |
| 4 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 |
| 5 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 |
| 6 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
现在我们有了一个简单的过程 P,可以指导一个简单的代理实现两个个位十进制数的加法。我们可以设计一个新的过程 P1 来实现三个个位十进制数的加法,如下图所示。
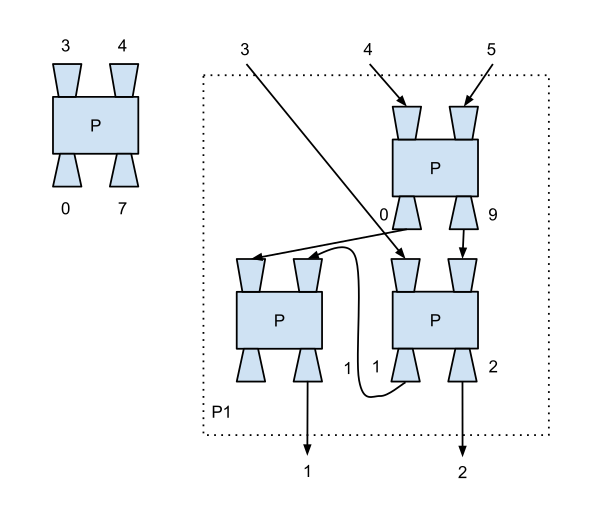
该图展示了如何通过过程 P 构建过程 P1。
新的过程 P1 使用了三个 P 的实例来完成三个十进制数的加法,并返回两个数字作为结果。我们可以将这些过程视为具有输入和输出的机器,而线条是允许符号从一个地方传递到另一个地方的“管道”。可以想象,能够执行 P 的代理也可以执行 P1,因为 P1 完全由 P 构成。图中虚线矩形表示由 P 的实例构成的新过程 P1,其对示例输入给出的答案是正确的。同样,在这个过程中使用的符号可以是任意一组符号,因为内部只执行了简单的表格查找。
现在想象一下,我们可以用 P1 构建更复杂的过程,例如下面图表中的 P2。
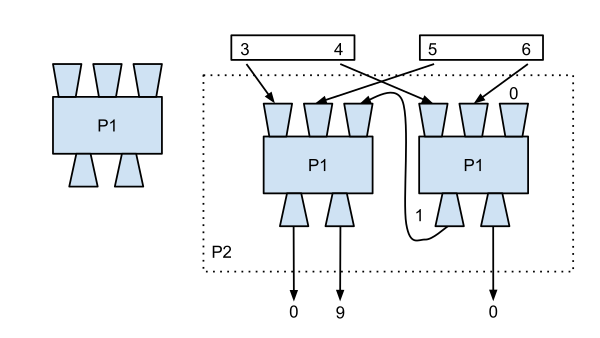
该图展示了如何通过 P1 构建 P2。
P2 使用 P1 实现了两个两位十进制数的加法。实际上,我们可以通过增加更多的 P1 来处理任意位数的数字。
到目前为止,我们可以得出以下结论:
- 能够执行 P 的机器同样可以执行 P1、P2 等过程。
- 我们通过构建更复杂的过程来完成看似智能的活动,同时保持这些过程能够由简单的机器完成。
- 如果沿着这一思路继续发展,我们可以创建越来越复杂的过程,指导简单的机器完成逐步更智能的任务,例如:
- 整数减法
- 比较两个整数(减法并检查结果符号)
- 整数乘法(重复加法)
- 使用一对整数表示分数并对其进行算术运算
- 使用整数矩阵表示方程组并通过矩阵运算求解
- 使用方程组建模复杂物理系统并对其进行数值模拟
总之,从这个例子中我们可以看到,通过计算过程,简单的符号操作可以组装成更大的过程来完成令人惊叹的活动。这些活动并不限于数值计算。如果我们能够将抽象思想表示为符号(就像将抽象数量表示为具体数字一样),并设计过程来根据思想之间的关系操作这些符号,我们就可以将推理建模为计算过程。这正是计算机科学的核心——信息处理包括两个基本组成部分:表示形式以及操作表示形式的一系列规则。请注意,这与电子学或物理学无关。执行这些过程的机器无需知道符号的含义或为什么过程会产生正确的结果。机器只需要盲目地遵循这些过程(规则集)即可。
示例
您可以了解由查尔斯·巴贝奇设计的一种机械计算机(差分机),它能够计算多项式函数的值:
差分机:计算多项式函数的解

另一个类比
理查德·费曼在他的《计算机启发式讲座》(时长1小时15分钟)中,使用了另一个类似的类比(文件管理员)来解释计算机是如何从内部工作到外部工作的:
历史
现在我们知道,计算本质上是对符号的一种特定操作。计算机能够完成令人惊叹的任务,其核心在于它按照明确规则操作符号的能力。实际上,数字计算机仅操作两种符号——0 和 1。计算的智能体现在规则/程序的设计与实现中。
未来,当我们谈论计算机硬件时,我们将看到计算机是基于这些原理构建的。
您可能会好奇这些想法的起源。在历史上,许多人对计算和计算机的理念做出了重要贡献。德国哲学家戈特弗里德·莱布尼茨(1646–1716)被认为是第一个梦想将推理转化为计算并构建能够执行此类计算的机器的人。他观察到,在算术中,我们用符号表示抽象数量,并根据规则操作符号以获得有用的结果。他设想,我们可以用符号表示抽象的思想,并通过类似于算术中具体符号操作的方式,根据思想之间的逻辑关系进行推理。这种操作得出正确结果的原因,不是操作者的聪明,而是因为操作规则反映了数量之间的关系和思想之间的逻辑。
由于莱布尼茨的梦想,我们今天有了计算机科学和被称为计算机的通用机器。计算机本质上是一种能够根据非常简单的逻辑规则操作符号的物理设备。几乎所有的计算机都是电子的,因为以这种方式构建成本更低、效率更高。计算机科学的核心是通过符号操作遵循某种规则(即算法)来进行信息处理(处理抽象思想)。难怪许多计算机编程书籍都被称为“食谱”!在计算机科学中,我们研究如何表示信息以及如何设计和应用算法以获得有意义的结果。同一任务通常有多种执行方式,对算法进行比较以评估其效果被称为算法(复杂性)分析。将算法(规则)传达给计算机的过程称为编程或软件开发。用于这种沟通的语言称为计算机编程语言。编程的成果是计算机程序或软件。为了在软件开发过程中生产高质量的软件,我们尝试应用的工程学科被称为软件工程。因此,计算机科学更多的是关于解决问题,而非仅仅研究计算机本身。事实上,“计算科学”可能是更贴切的学科名称。
计算实践
原理是贯穿计算各个方面的基本思想。实践虽然不是原理,但识别这些实践非常有用,因为它们定义了计算专业人士的核心技能。实践有时被称为“技能”,并定义了某人的能力水平:初学者、熟练者和专家。在“大计算原理”项目中,识别出了计算的四大核心实践:
- 编程(包括多语言编程实践)
- 系统与系统思维
- 建模、验证、测试和测量
- 创新
编程是计算机科学的重要组成部分,因为它让我们能够以具体的方式探索计算机科学中的抽象思想。它也是一项令人兴奋的创造性活动,当我们能够让计算机完成有用的任务时,会带来极大的满足感。在本课程中,我们将在一个非常高级的图形化编程环境中进行编程,以探索计算机科学中的各种思想。
唐纳德·克努斯(Donald Knuth)将编程比作创作:编写良好的程序对自己或他人来说都是一种享受。他认为编程有三重回报:
- 美观的代码(审美)
- 完成有用的工作(人道主义)
- 获得报酬(经济)
编程本质上是在教计算机如何执行任务。正如我们之前提到的,计算机是严格遵循指令的简单机器。为了让计算机执行正确的任务,我们程序中的指令必须是正确且逻辑的。可以在计算机上执行的程序被称为软件——它是计算机的大脑。存在错误的软件被称为“有漏洞(buggy)”的软件。通过在实际计算机上测试软件,可以捕捉到大多数软件中的漏洞。测试提供了对程序质量的几乎即时反馈,以便我们修复漏洞并改进程序。正因如此,我们认为编程使我们成为更优秀的思考者和学习者。我们将看到为什么证明程序的正确性是一件困难的事情。
参考资料
- Levesque, Hector,《作为计算的思维》,Hector J. Levesque,ISBN 9780262016995
- Denning, Peter,《大计算原理》,项目网址