计算机科学基础
抽象与递归
编程很简单,前提是程序规模较小。然而,当我们编写程序以解决越来越复杂的问题时,程序的规模会不可避免地增长。为了保持算法和程序的简单性,我们使用了一种强大的技术——抽象。抽象是一种广泛应用于艺术、数学和工程等领域的理念。本章将研究如何在算法设计和编程中应用这一技术。
什么是抽象?
抽象通过移除细节,帮助我们专注于关键内容。例如,一辆汽车向驾驶员提供了一组简单的控制界面。只要我们知道如何使用这些界面,就可以驾驶汽车,而无需了解其内部运作的细节。对于大多数司机来说,汽车的内部工作原理并不重要,但对于赛车手来说,这些知识可能是必要的。
这种界面自第一辆汽车制造以来几乎没有变化。抽象还通过提取共同特性从具体实例中进行概括。例如,汽车的驾驶界面抽取了所有汽车的共同特征(驾驶所需的知识),从而实现了对汽车的普遍适用性。学习驾驶一辆汽车后,驾驶相同类型的其他汽车就变得轻松。这一理念赋予汽车制造商在不影响用户的情况下更改汽车内部设计的自由。
计算中的抽象
算法设计是计算问题解决和编程的一个重要部分。编程的难点不在于代码编写本身,而在于如何在大型程序中跟踪和管理细节。
有两种主要方法可以让我们的程序保持“简洁”:
- 模块化(Chunking): 将功能分解为更小的单元(模块),并通过定义良好的接口让这些单元彼此交互。例如,在 Snap! 中,可以将算法实现为一个模块化的代码块,只需通过正确的参数调用接口即可随时在脚本中使用这个代码块。
- 分层(Layering): 将功能单元(代码块)分层以分离关注点,简化交互模式,从而更好地管理复杂性。下图说明了分层的概念:
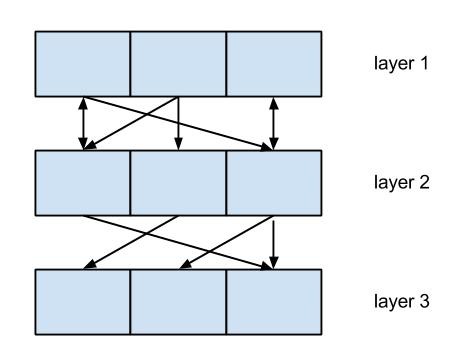
图例:分层示意图
在分层结构中,每一层依赖其下方的层实现功能,并为上方的层提供服务。例如,位于第一层的单元只能调用第二层的单元。所有交互仅限于相邻层之间。我们可以完全替换某一层的实现而不影响整个系统,这实现了模块化。
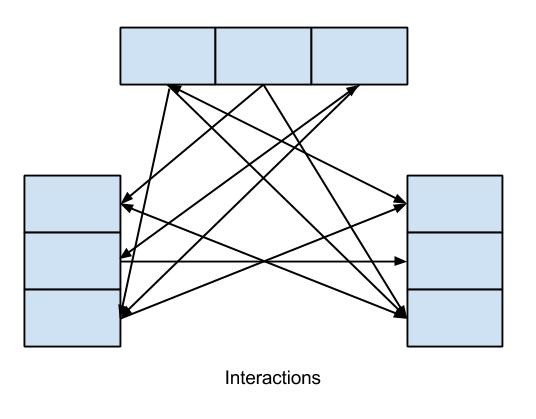
如果没有分层限制,系统可能变成如下图所示的紧耦合系统:
图例:无分层的紧耦合示意图
在紧耦合系统中,任意单元可以随意调用其他单元,导致系统复杂难以维护。
抽象实例
通过抽象实现简化和概括是一个强大的组织理念。回想第一章中的思想实验,我们构建了一台能够解方程组的机器。该机器正是通过抽象构建的——我们使用更基础的单元构造了更大的构建块,并将每个块视为一个独立单元,忽略其内部细节。
在 Snap! 环境中,我们可以以类似的方式构造程序。当定义一个代码块时,它就变成了一个新的构建模块(用户自定义模块)。无论这个代码块有多复杂,使用时我们只需知道它的接口——包括名称和参数列表。隐藏不必要的细节极大地简化了编程中的思维过程。
示例:绘制等边图形的模块
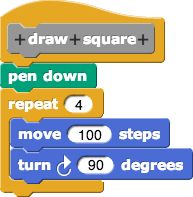
为了让一个角色绘制不同的等边图形,我们可以为每种形状(如三角形、正方形、五边形等)创建一个代码块。在 Snap! 中,一个代码块是一个抽象体,隐藏了具体的实现细节,代表特定的行为或意图。以下代码块用于绘制一个指定大小的正方形:
图例:Snap! 中绘制正方形的代码块
这个代码块接受一个大小参数并绘制一个正方形。通过抽象,我们可以将复杂的行为封装成单一的代码块,从而简化程序设计。
计算机科学基础:抽象与递归
编程的抽象与递归
当程序规模较小时,编程相对简单。然而,随着我们为解决更复杂的问题而创建程序,其规模会不可避免地扩大。为了让我们的算法和程序保持简单,我们采用了一种强大的技术——抽象。抽象是一种广泛应用于艺术、数学和工程等领域的理念。本章将研究如何在算法设计和编程中应用抽象这一技术。
什么是抽象?
抽象通过移除细节帮助我们专注于关键内容。例如,一辆汽车为驾驶员提供了一套简单的控制界面。只要我们了解如何操作这些界面,就可以驾驶汽车,而不需要了解其内部的运作原理。对于大多数驾驶员来说,汽车内部的运作原理并不重要,除非是赛车手需要通过这些知识更高效地驾驶汽车。
这种界面从第一辆汽车问世以来几乎没有发生过变化。抽象还通过提取共同特性将具体实例进行概括。例如,汽车的驾驶界面提取了所有汽车的共同特性(驾驶所需的知识),从而对不同类型的汽车具有普遍适用性。一旦学会驾驶一种汽车,就基本能够驾驶同类型的所有汽车。这种抽象不仅为用户提供便利,也为汽车制造商在不影响用户体验的前提下更改汽车内部设计提供了自由。
计算中的抽象
在解决计算问题时,算法设计是一个不可或缺的部分,也是编程的第一步。编程的难点并不在于代码的编写,而在于如何在大型程序中管理细节。
有两种主要方法可以让程序保持“简洁”:
- 模块化(Chunking): 将功能分解为更小的单元,并通过定义良好的接口让这些单元彼此交互。例如,在 Snap! 中,可以将算法实现为一个代码块,只需通过正确的参数调用接口即可在脚本中随时使用该代码块。
- 分层(Layering): 将功能单元(代码块)分层以分离关注点,简化交互模式,从而更好地管理复杂性。下图展示了分层的概念:
分层示意图
每一层依赖其下方的层来实现功能,同时为上方的层提供服务。例如,位于第一层的单元只能调用第二层的单元。所有交互仅限于相邻层之间。分层使我们能够替换某一层的实现而不影响整个系统,从而实现模块化。
如果没有分层的限制,系统可能变得如以下所示,成为紧耦合系统:
紧耦合示意图
在紧耦合系统中,任意单元可以随意调用其他单元,导致系统复杂且难以维护。
抽象实例
通过抽象实现简化和概括是一种强大的组织理念。回想第一章中的思想实验:我们构建了一台能够解方程组的机器。该机器正是通过抽象构建的——使用更基础的单元构造更大的构建块,并将每个块视为一个独立单元,忽略其内部细节。
在 Snap! 环境中,我们可以以类似的方式构造程序。当定义一个代码块时,它就成为一个新的构建模块(用户自定义模块)。无论这个代码块有多复杂,使用时我们只需知道它的接口——包括名称和参数列表。隐藏不必要的细节极大地简化了编程中的思维过程。
示例:绘制等边图形的模块
为了让角色绘制不同的等边图形,我们可以为每种形状(如三角形、正方形、五边形等)创建一个代码块。在 Snap! 中,一个代码块是一个抽象体,隐藏了具体的实现细节,代表特定的行为或意图。
以下代码块用于绘制一个指定大小的正方形:
绘制正方形的 Snap! 代码块
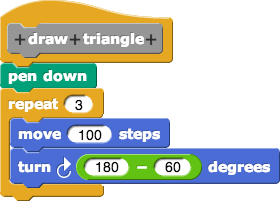
类似地,可以使用以下逻辑绘制一个等边三角形:
绘制三角形的 Snap! 代码块
该代码块通过重复三次绘制每条边,并在每次绘制后旋转 120 度来形成三角形。你是否知道为什么旋转 120 度能够形成 60 度的内角?
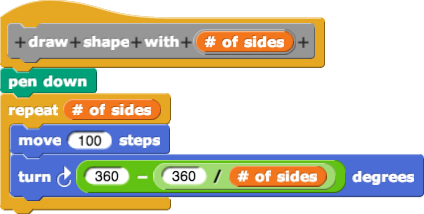
通过这种方式,我们可以进一步抽象任务,创建一个可以绘制任意等边图形的代码块:

绘制任意等边图形的 Snap! 代码块
通过此示例,我们展示了如何通过定义代码块来抽象任务的细节,并将解决方案概括为适用于更多问题的通用形式。
递归
递归是一种自相似的模式——整体由与整体结构相似的更小部分组成。例如,一棵树由看起来像小树的树枝组成。类似地,计算机文件系统的目录树和家谱的祖先树也展示了这种模式。
递归的美在于可以以更简洁和优雅的方式定义具有这种模式的概念。例如,树的定义可以是:要么是没有树枝的树干,要么是带有若干树枝(每根树枝也是一棵树)的树干。
示例:递归定义的树形结构与递归画图
通过递归思维解决问题可以简化思考过程:如果你能递归地定义一个问题,那么你也可以递归地解决它。递归解决方案优雅且易于验证,但仅适用于可以递归定义的问题。
递归是计算机科学中的一项强大技术,后续我们将通过更多示例进一步探讨其应用。
绘制三角形
我们可以使用类似的逻辑结构来绘制一个等边三角形。
此 Snap! 代码块可以绘制一个等边三角形。
该绘制三角形的代码块重复三次,每次绘制一条边并旋转 120 度。你知道为什么角色需要旋转 120 度以形成两条边之间的 60 度角吗?希望你已经注意到,相同的逻辑结构可以用来创建绘制任意等边形的代码块。与其为每种形状单独创建一个代码块,不如将任务概括为一个通用的代码块,可以绘制任意形状。这个代码块需要额外的一条信息——边的数量。
此 Snap! 代码块可以绘制任意等边形。
根据边的数量,我们可以确定形状的内角,而这正是绘制形状所需的全部信息。如果你不确定如何通过边数计算内角,可以参考相关资源。
此代码块可以作为绘制等边形(多边形)任务的抽象。你可能已经注意到边长是硬编码的(作为常量输入),如果我们希望绘制不同大小的形状怎么办?可以进一步将代码块的功能泛化,增加一个参数,用以控制边长。
此 Snap! 代码块可以绘制任意大小的等边多边形。
通过这个示例,我们展示了如何定义代码块以抽象化任务的细节,并将解决方案泛化为能够解决更多问题的通用形式。
递归
递归是一种自相似的模式——整体由与整体结构相似的更小部分组成。例如,一棵树由看起来像小树的树枝组成。同样,计算机文件系统中的目录树和家谱中的祖先树也体现了这种模式。
递归树
使用 Logo 编程语言创建的递归树形结构。
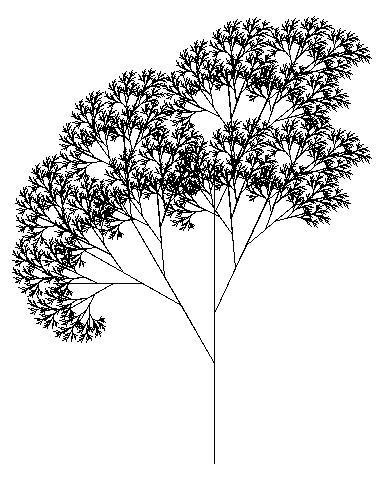
自相似性允许我们用更简洁和优雅的方式定义这种模式的概念。一棵树可以是没有树枝的树干,或者是带有若干树枝(每根树枝也是一棵树)的树干。这种定义涵盖了所有可能的树结构。
递归解决问题
如果我们正在解决的问题是自相似的——解决整个问题只需解决与整体相似的部分问题——那么我们为整体定义的解决方案就可以用于解决子问题(这就是递归)。递归解决方案的美妙之处在于,问题的定义本身就是解决方案,例如阶乘函数:
- 1!=11! = 1
- 对于所有 n>1n > 1:n!=n×(n−1)!n! = n \times (n-1)!
这种递归定义不仅定义了阶乘,还描述了计算阶乘的方法。例如,计算 5!5! 可以通过 4!4! 得出,依次类推,直到 1!1! 根据定义等于 1。
设计递归解决方案
设计递归解决方案时,我们采用“愿景思维”(wishful thinking)——在描述整体问题的解决方案时,希望其已经完全定义并可以用于解决更小的子问题。在编程中,这被称为递归思维或递归编程。
递归编程通过以下方式描述问题的解决方案:
- 将更大的问题分解为更小的问题。
- 使用当前定义的函数/过程/代码块来解决这些更小的问题。
如果问题是有限的,最终会达到一些直接可解的简单问题。这些简单问题称为基准情况(base cases)。当程序到达所有基准情况时,整个问题就得以解决,因为所有子问题,包括最初的问题,都已解决。
递归函数的两部分
任何递归函数都必须包含两个基本部分:
- 基准情况(base cases): 停止递归,通过直接解决简单问题结束递归。
- 递归情况(recursive cases): 将较大的问题分解为更小的问题。
只要这两个部分都存在且结构合理,该算法(函数)就可以通过自身克隆解决任意规模的问题。递归问题解决是一种强大的方法,因为它简化了思考过程:如果你能递归地定义一个问题,那么你也可以递归地解决它。递归解决方案通常更优雅且易于验证,但它仅适用于可以递归定义的问题。

递归示例
以下是二分查找算法的例子:
在一个已排序的列表中查找目标项(target):
- 如果列表为空,目标项无法找到。
- 考虑列表中间的项,如果它与目标项匹配,则完成查找。
- 否则,决定下一步要搜索哪一半的列表。
在已排序列表的一半中继续搜索,其实是整个问题的一个更小版本/部分,因此我们可以应用相同的算法(假设算法已经完全定义)。这个过程会一直进行,直到列表为空或找到搜索目标为止。
基准情况(base cases):
- 如果列表为空,则目标项无法找到。
- 如果目标项位于列表的中间,则目标项已找到。
递归情况(recursive cases):
- 如果列表中间的项小于搜索目标,则在列表的后半部分继续搜索。
- 否则,在列表的前半部分继续搜索。
通过递归,每次缩小搜索范围并重复同样的算法,直至满足基准情况为止。这种递归的方式使二分查找高效地处理了排序列表的搜索问题。