If you haven't previously studied 3D graphics, technical drawing, or analytic geometry, you are about to learn a new way of visualizing the world, an ability that's fundamental to working with Blender or any 3D modeling tool.
::如果你以前没有学习过3D图形,技术绘图或分析几何学,

3D modeling is based on geometry, the branch of mathematics concerned with spatial relationships, specifically analytical geometry, which expresses these relationships in terms of algebraic formulas. If you have studied geometry, some of the terminology will be familiar.
::立体模型是基于几何学,数学的分支涉及空间关系,特别是分析几何学,它用代数公式来表达这些关系. 如果你学过几何学,你会熟悉一些术语.

Coordinates And Coordinate Systems

Look around the room you’re in. The odds are it will have a cuboidal shape, with four vertical walls at right angles to each other, a flat, horizontal floor, and a flat, horizontal ceiling.
::房间的形状很可能是立方体,四个垂直的墙壁彼此直角,平坦的水平地板和平坦的水平天花板.

Now imagine there’s a fly buzzing around the room. The fly is moving in three-dimensional space. In mathematical terms, that means its position within the room at any given moment, can be expressed in terms of a unique combination of three numbers.
::现在想象一下,有一个在房间里. 它在三维空间中移动. 通过数学术语,这意味着它在房间中的位置在任何给定的时刻,都可以用三个数字的独特组合来表达.

There are an infinite number of ways — coordinate systems — in which we could come up with a convention for defining and measuring these numbers, i.e. the  coordinates . Each convention will yield different values even if the fly is in the same position. Coordinates only make sense with reference to a specific coordinate system! To narrow down the possibilities (in a purely arbitrary fashion), let us label the walls of the room with the points of the compass: in a clockwise direction, North, East, South and West. (If you know which way really is north, feel free to use that to label the walls of your room. Otherwise, choose any wall you like as north.)
::有无数种方法可以定义和测量这些数字,即坐标.即使苍蝇处于相同位置,每个规则也会产生不同的值.坐标只与特定坐标系统相关!为了缩小可能性 (以纯粹任意的方式),让我们用指南针的点标记房间的墙壁:顺时针方向,北,东,南和西. (如果你知道哪个方向是北,请随意使用它来标记你的房间的墙壁.否则,选择任何你喜欢的墙壁作为北.

Consider the point at floor level in the south-west corner of the room. We will call this (arbitrary) point the  origin  of our coordinate system, and the three numbers at this point will be  ( 0 , 0 , 0 ) . The first of the three numbers will be the distance (in some suitable units, let’s say metres) eastwards from the west wall, the second number will be the distance north from the south wall, and the third number will be the height above the floor.
::考虑一下房间西南角的地板水平的点.我们将这个 (任意) 点称为我们坐标系的起源,这个点的三个数字将是 (0,0,0).这三个数字中的第一个数字将是距离 (在一些合适的单位,比如米) 从西墙向东,第二个数字将是距离南墙向北的距离,第三个数字将是地板上的高度.

Each of these directions is called an  axis  (plural:  axes ), and they are conventionally labelled X, Y and Z, in that order. With a little bit of thought, you should be able to convince yourself that every point within the space of your room corresponds to exactly one set of  ( x , y , z )  values, and that every possible combination of  ( x , y , z )  values, with  0 ≤ x ≤ W ,  0 ≤ y ≤ L  and  0 ≤ z ≤ H  (where  W  is the east-west dimension of your room,  L  is its north-south dimension, and  H  is the height between ceiling and floor) corresponds to a point in the room.
::这些方向的每个方向被称为轴 (复数:轴),它们通常以X,Y和Z的顺序标记.有点思考,你应该能够说服自己,你的房间空间中的每个点都与 (x,y,z) 值的正确一组相对应,并且 (x,y,z) 值的每个可能组合,其中0 ≤ x ≤ W,0 ≤ y ≤ L和0 ≤ z ≤ H (其中W是你的房间的东-西维度,L是它的北-南维度,H是天花板和地板之间的高度) 与房间中的一个点相对应.

The following diagram illustrates how the coordinates are built up, using the same colour codes that Blender uses to label its axes: red for X, green for Y and blue for Z (an easy way to remember this if you're familiar with RGB is the order -- Red X, Green Y, Blue Z). In the second picture, the  x  value defines a plane parallel to the west wall of the room. In the third picture, the  y  value defines a plane parallel to the south wall, and in the fourth picture, the  z  value defines a plane parallel to the floor. Put the planes together in the fifth picture, and they intersect at a unique point.
::下图说明了坐标是如何构建的,使用相同的颜色代码,Blender使用标记它的轴:红色为X,绿色为Y和蓝色为Z (如果你熟悉RGB,一个简单的方法来记住这个是顺序 - - 红色X,绿色Y,蓝色Z).在第二张图中,x值定义了一个平面平行于房间的西墙.在第三张图中,y值定义了一个平面平行于南墙,在第四张图中,z值定义了一个平面平行于地板.在第五张图中把平面放在一起,它们交于一个独特的点.在第五张图中,x值定义了一个平面平行于房间的西墙,而z值定义了一个平面平行于地板.在第五张图中,x值

Another simple way to understand what the coordinates of a point say (x,y,z) means is, if one starts from origin and moves x, y, and z units of distance parallel to x, y, and z axes respectively, in any sequence, one will reach that point. Thus, for example, a coordinate of (3,4,5) means the point which is reached when one moves, starting from origin, 3 units of distance along x-axis, 4 units of distance along y-axis and 5 units of distance along z-axis.
::了解一个点的坐标 (x,y,z) 的意思的另一个简单方法是,如果从原点开始,并以任何顺序移动x,y和z单位的距离并行于x,y和z轴,则会到达该点.因此,例如,坐标 (3,4,5) 代表一个点在移动时达到的点,从原点开始,沿x轴走3个单位的距离,沿y轴走4个单位的距离和沿z轴走5个单位的距离.

This style of coordinate system, with the numbers corresponding to distances along perpendicular axes, is called  Cartesian coordinates , named after René Descartes, the 17th-century mathematician who first introduced the concept. Legend has it that he came up with the idea after watching a fly buzzing around his bedroom!
::这种坐标系的形式,数字与垂直轴上的距离相对应,被称为卡特斯坐标,以17 世纪数学家雷内·笛卡尔的名字命名,他首次提出了这个概念.传说说,他看到了一只在他的卧室里!

There are other ways to define coordinate systems, for example by substituting direction angles in place of one or two of the distance measurements. These can be useful in certain situations, but usually all coordinate systems in Blender are Cartesian. However, in Blender, switching between these coordinate systems is simple and easy to do.
::定义坐标系还有其他方法,例如在某种情况下可以使用方向角代替一两个距离测量.但通常在Blender中所有的坐标系都是卡特的.然而,在Blender中,在这些坐标系之间切换是简单的.

Negative Coordinates
::负坐标

Can coordinate values be negative? Depending on the situation, yes. Here we are only considering points within our room. But suppose instead of placing our origin in the bottom southwest corner, we put it in the middle of the room, halfway between the floor and ceiling. (After all, it is an arbitrary point, we can place it wherever we like, as long as we agree on its location.) If the X-coordinate is the distance  east  from the origin, how do we define a point  west  of the origin? We simply give it a negative X-coordinate. Similarly, points north of the origin have a positive Y-coordinate, those south of it, have negative Y-coordinates. Points above the origin have a positive Z-coordinate, those below it, a negative Z-coordinate.
::坐标值可以是负的吗? 取决于情况,是的. 这里我们只考虑房间内的点. 但假设我们不把我们的原点放在下面的西南角,而是把它放在房间的中间,在地板和天花板之间. (毕竟,它是一个任意的点,我们可以把它放在我们喜欢的地方,只要我们同意它的位置. 如果X坐标是从原点到东的距离,我们如何定义一个点从原点到西? 我们只是给它一个负的X坐标. 同样,原点的北方有正的Y坐标,南方的有负的Y坐标. 原点以上的点有正的Z坐标,下面的有负的Z坐标.

Handedness Of Coordinate Systems
::坐标系的手性

It is conventional for most Cartesian coordinate systems to be  right-handed . To understand this, hold the thumb, index finger and middle finger of your right hand perpendicular to each other:
::大多数笛卡尔坐标系都是右手的.为了理解这一点,请将右手的指,食指和中指垂直对齐:

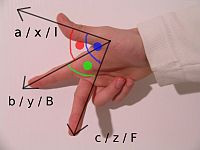
Figure 1:  The three axes form a right-handed system

Now orient your hand so your thumb points along the X-axis in the positive direction (direction of increasing coordinate numbers), your index finger along the positive Y-axis, and your middle finger along the positive Z-axis. Another way of looking at it is, if you placed your eye at the origin, and you could see the three arrows pointing in the directions of positive X, positive Y and positive Z as in Figure 1, the order X, Y, Z would go counter clockwise.
::现在把手指指向正方向沿着X轴 (增加坐标数的方向), 指向指沿着正Y轴, 中指沿着正Z轴. 另一个看法是,如果你把眼睛放在原点,你可以看到三个箭头指向正X,正Y和正Z的方向,如图1所示,X,Y,Z的顺序将与时针针针相反.

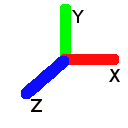
Figure 2:  Another view of right-handed system

Another way to visualize this is to make a fist with your right hand, with your curled fingers towards you. Stick out your thumb directly to the right (X). Now aim your pointer finger straight up (Y). Finally, make your middle finger point toward yourself (Z). This is the view from directly above the origin.
::另一个可视化方式是用右手拳头,把手指曲向你.把指伸向右 (X).现在把手指指向上 (Y).最后,让中指指向自己 (Z).这是从原点上方的视图.

Axes Of Rotation

Consider a spinning sphere. Every point on it is moving, except the ones along the axis. These form a motionless line around which the rest of the sphere spins. This line is called the  axis of rotation .
::想象一下旋转的球体.它上的每个点都在运动,除了沿着轴的点.这些点形成一个不动的直线,其余的球体围绕着它旋转.这个直线被称为旋转轴.

More precisely, the axis of rotation is a point or a line connecting points that do not change position while that object rotates, drawn when the observer assumes he/she does not change position relative to that object over time.
::更准确地说,旋转轴是一个点或连接点的线,在物体旋转时不改变位置,当观察者假定他/她不会随着时间的推移改变相对于该物体的位置时,他/她会画出该点.

Conventionally, the  direction  of the axis of rotation is such that if you look in that direction, the rotation appears clockwise, as illustrated below, where the yellow arrow shows the rotational movement, while the purple one shows the rotation axis:
::传统上,旋转轴的方向是这样的,如果你朝着这个方向看,旋转就会以时针方向出现,如下图所示,黄色箭头显示旋转运动,而紫色的箭头显示旋转轴:

To remember this convention, hold your right hand in a thumbs-up gesture:
::为了记住这个惯例,请举起右手,举起指:

If the rotation follows the direction of your curled fingers, then the direction of the axis of rotation is considered to be the same as the direction which the thumb is pointing in.
::如果旋转跟随曲的手指的方向,则旋转轴的方向被认为与指指向的方向相同.

This gesture is a different form of the right-hand rule and is sometimes called  the right-hand grip rule ,  the corkscrew-rule  or  the right-hand thumb rule . From now on we will refer to it as 'the right-hand grip rule'.
::这种手势是右手规则的另一种形式,有时被称为右手握法,拉杆法或右手指法.从现在起,我们将称之为"右手握法".

When describing the direction of a rotating object, do not say that it rotates  left-to-right/clockwise , or  right-to-left/counterclockwise . Each of these on their own are meaningless, because they're relative to the observer. Instead of saying this, find the direction of the axis of rotation and draw an arrow to represent it. Those who know the right-hand grip rule will be able to figure out what the direction of rotation of the object is, by using the rule when interpreting your drawing.
::在描述旋转物体的方向时,不要说它旋转左向右/时钟针方向,或右向左/反时钟方向.这些都是无意义的,因为它们与观察者相对.而不是说这,找到旋转轴的方向并画一个箭头来表示它.那些知道右手握法的人将能够通过使用规则来解释你的图画,来弄清楚物体的旋转方向是什么.

最后修改: 2025年03月11日 星期二 16:41