Coordinate Transformations

坐标变换

A  transformation  is any operation that changes coordinate values in some way. For example, if you pick up an object and move it to a different place in the room without changing its orientation, then the coordinates of each point on the object relative to the room are adjusted by an amount that depends on the distance and direction between the old and new positions. This is called a  translation  transformation.
::转换是以某种方式改变坐标值的任何操作.例如,如果你拿起一个物体并将其移到房间的不同位置而不改变其方向,那么对象的每个点相对于房间的坐标都会根据旧位置和新位置之间的距离和方向进行调整.这被称为转换转换.

Object at original location
Object translated to new position


Simply turning the object without moving it from its original location is called  rotation .
::简单地转动一个物体而不移动它从原来的位置被称为旋转.

Object rotated 45°


If the object were to get bigger or smaller, that is a  scaling  transformation. In the real world, only a few objects can be scaled in this way. For example, a balloon can be inflated or deflated to a larger or smaller size, but a bowling ball cannot. Regardless of what can and can't be re-sized in the real world, any object can be scaled (re-sized) in the world of computer graphics. Scaling may be  uniform , i.e. apply equally in all dimensions, or  non-uniform .
::如果物体变大或变小,那就是一个缩放转换.在现实世界中,只有少数物体可以以这种方式进行缩放.例如,气球可以被膨胀或放气到更大或更小的尺寸,但保龄球不能.无论在现实世界中可以和不能重新缩放什么,任何物体都可以在计算机图形世界中进行缩放 (重新缩放).缩放可能是均的,即在所有维度中均适用,或非均.

Object uniformly scaled to 50% of original size
Object scaled vertically to 50% of original size


Linear Transformations

The main types of coordinate transformations we’re concerned with are called  linear transformations . Lines that were straight before the transformation remain straight. i.e. they do not become curved. For example, the following diagram illustrates three linear transformations applied to the square in the center: Clockwise from the left, a  shear  or  skew , a scale, and a rotation, plus one non-linear transformation that causes two sides of the box to become curved.
::我们所关注的坐标转换的主要类型称为线性转换.转换前直线的线保持直线,即它们不会变曲.例如,下图说明了三种应用到中心方形的线性转换:从左向时针方向,剪切或斜,尺度和旋转,以及导致盒子两侧变曲的非线性转换.

Multiple Transformations

多个转换

It is possible to  concatenate  or  compose  a series of transformations. The resulting transformation can do many things in one operation — translation, rotation, scaling etc. However, the order of composition of the component transformations becomes important. In general, transformations are not  commutative . For example, compare the result of moving our model some distance along the Y axis followed by rotating it about the X axis (If this doesn't make sense, consider that the axes are fixed, they aren't moving with the object. More on that later  Global and local coordinates ):
::连接或组合一系列的转换是可能的. 结果的转换可以在一个操作中做很多事情转换,旋转,缩放等. 然而,组件转换的组合顺序变得很重要. 一般来说,转换不是可换的. 例如,比较我们的模型沿Y轴移动一段距离,然后旋转它绕X轴的结果 (如果这不 masuk akal,请考虑轴是固定的,它们不是随着物体移动. 稍后更多关于全球和本地坐标):

Translation followed by rotation

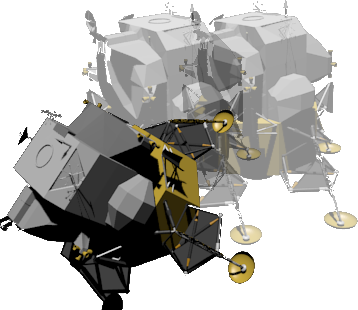
versus the result of doing the rotation first:
::与首先做旋转的结果:

Rotation followed by translation

In some instances, the three forms of transformation may be applied on a single object concurrently. Such a feature exists in Blender and is normally implemented in creating animations. For example, you can decide to pick up the object (first transformation - translation), twist it (second transformation - rotation), and, in a 3D modeling environment, increase the size of the object (third transformation - scaling).
::在某些情况下,三种形式的转换可能同时应用于单个对象.这种功能存在于混器中,通常用于创建动画.例如,您可以决定取出对象 (第一个转换 - 转换),扭曲它 (第二个转换 - 旋转),并在3D建模环境中增加对象的大小 (第三个转换 - 缩放).

Inverse Transformations

逆变换

Often there is a need to find the  inverse  of a transformation. That is, a transformation that has the opposite effect. For example, a rotation of +45° about the X axis is undone by a rotation of -45° around the same axis.
::通常需要找到一个变化的反向.即,一个具有相反效果的变化.例如,围绕X轴旋转+45°的转变被围绕同一轴旋转-45°取消.

Inverses have many uses, one of which is to simplify the construction of certain kinds of transformations.
::逆数有很多用途,其中一个是简化某些类型的变换的构造.

For example, it is easy to construct a rotation transformation about the X, Y or Z-axis of the coordinate system. But what about a rotation of Θ° around an arbitrary axis? This can be made out of the following parts:
::例如,很容易构建一个关于坐标系的X,Y或Z轴的旋转转换.但是,关于 Θ° 绕任意轴的旋转呢?这可以由以下部分构成:

  • a translation that makes the rotation axis pass through the origin.
    ::转移使旋转轴通过原点.
  • rotations about the Y and/or Z axes, as appropriate, so the rotation axis lies along the X axis.
    ::根据情况,围绕Y和/或Z轴的旋转,所以旋转轴沿着X轴.
  • a rotation of Θ° about the X axis.
    ::一个关于X轴的 Θ° 旋转.
  • the inverse of the rotations that aligned the rotation axis with the X axis.
    ::旋转轴与X轴对齐的反转.
  • the inverse of the translation that made the rotation axis pass through the origin.
    ::转移的反向使旋转轴通过原点.

Most of the transformations we deal with in 3D modelling have an inverse, but not all. See the next section for some that don’t.
::大多数我们在3D建模中处理的转换都有反向,但不是所有.请参阅下一节,以了解一些没有反向的转换.

Projections

投影

Most of our display and output devices are not three-dimensional. Thus, three-dimensional images need to be  projected  onto a two-dimensional surface (like a display screen or a printed page) before we can see them.
::我们的显示器和输出设备大多不是三维的.因此,我们需要将三维图像投射到二维表面 (如显示屏或印刷页面) 才能看到它们.

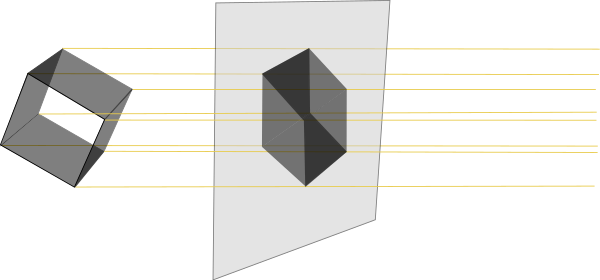
There are two main ways to perform such projections. One is  orthographic  projection, where parallel lines are drawn from all points of the three-dimensional object until they intersect a plane representing the display surface:
::进行此类投影有两种主要方法. 一种是正写投影,其中平行线从三维物体的所有点绘制,直到它们交叉表示显示表面的平面:

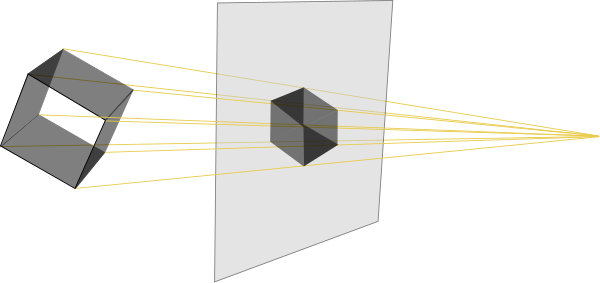
The other method is  perspective  projection, where the lines drawn are not parallel, but intersect at a point representing the location of the eye of the viewer:
::另一种方法是透视投影,画的线条不是平行,而是交于代表观众眼睛位置的点:

Projections are also linear transformations. But since they take a three-dimensional space and flatten it onto a two-dimensional surface, some information is lost. Those transformations are irreversible i.e. they cannot be undone, at least in a unique way as the depth information is gone.
::投影也是线性转换.但是由于它们占用了三维空间并将其平整到二维表面,所以一些信息会丢失.这些转换是不可逆转的,即它们不能被撤销,至少在一个独特的方式,因为深度信息已经消失了.

You will read more about both orthographic and perspective views in the following pages.
::您将在下面的页面上阅读更多关于正写和视角的观点.

The mathematics of perspective were first worked out in the 11th century by  Alhazen , and used to great effect by the Italian Renaissance painters four hundred years later.
::视角的数学首先由阿尔哈森在11世纪开发出来,四百年后,意大利文艺复兴时期的画家们也非常有效地使用它.


Last modified: Tuesday, 11 March 2025, 4:49 PM