MATLAB编程-简介
MATLAB 中的函数介绍
函数是一组顺序执行的表达式语句(也可视作伪算法),组合在一起以完成一个任务。在 MATLAB 中,函数需定义在单独的文件中,且文件名必须与函数名相同。
函数在局部工作区(local workspace)中运行,该工作区独立于命令行窗口中访问的基础工作区(base workspace)。
函数可以接受多个输入参数,也可以返回多个输出参数。
函数的语法格式如下:
function [y1,...,yN] = myfunc(x1,...,xM)
这表示定义了一个名为 myfunc 的函数,接收输入参数 x1,...,xM,返回输出 y1,...,yN。
该函数定义语句必须是函数文件中第一条可执行语句,函数名必须以字母开头,可包含字母、数字或下划线。
在单独文件中创建函数
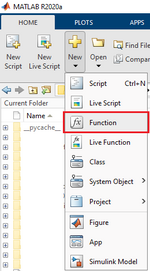 在 MATLAB "Home" 选项卡中点击 "New" → "Function",将自动生成如下模板:
在 MATLAB "Home" 选项卡中点击 "New" → "Function",将自动生成如下模板:
function [outputArg1,outputArg2] = untitled2(inputArg1,inputArg2)
%UNTITLED2 此函数的简要说明
% 更详细的说明在这里编写
outputArg1 = inputArg1;
outputArg2 = inputArg2;
end
声明一个函数示例
假设你所在的班级来了几位美国的交换生,他们抱怨天气太热,说温度高达 100 华氏度。作为习惯用摄氏度的人,你会想知道这到底是多少摄氏度?
于是我们可以写一个函数来完成华氏度到摄氏度的转换。
转换公式为:
°C = (°F - 32) * 5/9
新建函数文件,代码如下:
function [Ce] = convertTemp(Fa)
% 将华氏度转换为摄氏度
Ce = (Fa-32)*(5/9);
end
保存文件为 convertTemp.m(文件名必须与函数名相同)。
在命令窗口中调用此函数:
>> convertTemp(100)
ans =
37.7778
使用函数的好处
使用函数可以节省大量重复计算的工作,只需输入函数名和参数即可得到结果,避免重复输入公式。
MATLAB 中的函数类型
-
匿名函数(Anonymous Functions)
-
局部函数(Local Functions)
-
嵌套函数(Nested Functions)
-
私有函数(Private Functions)
-
内联函数(已废弃)
匿名函数
匿名函数不需要创建独立的 .m 文件,仅由单条表达式组成。
语法:
f = @(x) expression
示例:将华氏度转换为摄氏度:
>> convTempF = @(Fa) (Fa-32)*(5/9);
>> convTempF(88)
ans = 31.1111
示例:将分钟转换为秒:
>> convert_min_to_s = @(t) t*60;
>> convert_min_to_s(4)
ans = 240
局部函数(Local Functions)
一个 .m 文件中可以包含多个函数。第一个为主函数(main function),其余为局部函数。局部函数仅对同一个文件中的其他函数可见,类似于其他语言中的子程序(subroutines)。
示例:统计函数 statistik,输出最大值、最小值、平均值、标准差:
function [mx, mn, avg, stdv] = statistik(numbers)
% 统计函数:返回最大值、最小值、平均值和标准差
mx = getMax(numbers);
mn = getMin(numbers);
avg = getAverage(numbers);
stdv = getStd(numbers);
end
function m = getMax(x)
m = max(x);
end
function m = getMin(x)
m = min(x);
end
function a = getAverage(x)
a = sum(x)/length(x);
end
function s = getStd(x)
s = std(x);
end
然后在命令行调用:
>> [mx, mn, avg, stdv] = statistik([2, 4, 6, 8, 10])
MATLAB 函数详解翻译
创建统计函数(statistik)
首先,我们需要创建一个名为 statistik 的函数,具体步骤参考“在单独文件中创建函数”部分。
function [max,min,ave,stdev] = statistik(v)
% 主函数,调用局部函数,输入为一组数值向量 v,返回最大值、最小值、平均值和标准差
max = maxf(v);
min = minf(v);
ave = avef(v);
stdev = stdevf(v);
end
function a = maxf(v)
% 返回最大值
a = max(v);
end
function b = minf(v)
% 返回最小值
b = min(v);
end
function c = avef(v)
% 计算平均值
c = mean(v);
end
function d = stdevf(v)
% 计算标准差
d = std(v);
end
在命令窗口测试:
>> V = randi(50,1,10)
V =
25 29 12 23 49 28 27 12 25 32
>> [maximum,minimum,average,stdeviation] = statistik(V)
maximum =
49
minimum =
12
average =
26.2000
stdeviation =
10.4435
注意:虽然无法从命令行或其他文件中调用局部函数,但你可以使用 help 命令查看帮助:
>> help statistik>avef
嵌套函数(Nested Functions)
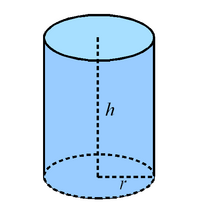 圆柱形金属锭
圆柱形金属锭

嵌套函数是定义在主函数内部的函数。与局部函数不同的是,嵌套函数可以访问其外部主函数中的变量,无需作为参数显式传入。
嵌套函数要求:
-
文件中所有函数都必须使用
end结束。 -
不能将嵌套函数定义在流程控制语句中(如
if、switch、for、while等)。 -
嵌套函数可以直接通过函数名或通过
@符号创建函数句柄调用。 -
所有变量必须在函数内部显式定义,不能依赖其他脚本设置的变量。
我们有一个假设情境:需要估算一块圆柱形金属锭的重量。
首先,在计算金属锭重量之前,我们需要将这个问题拆解为更小的步骤。
为了求出金属的重量,我们需要知道密度,而在求密度之前,我们需要先求出金属的体积。
步骤分解如下:
-
计算底面圆的面积
圆的面积公式为:
其中 是圆的半径。
-
利用底面积计算圆柱体体积
圆柱体积公式为:
其中 是圆柱的高度。
-
计算重量
重量计算公式为:
其中 是金属的密度。
MATLAB 函数缩进提示:
在 MATLAB 中编写上述公式时,**嵌套函数(Nested Functions)**必须进行缩进。
提示:可以通过 MATLAB 编辑器顶部菜单:
Editor -> Indent自动缩进嵌套函数。
示例:计算圆柱形金属锭的重量
function [] = ingot_calc()
r = 3; % 半径
h = 10; % 高度
d = 4.5;% 密度
ar = circle_area;
vo = volume;
we = weight;
function a = circle_area
a = pi*r^2;
disp(['Area of circle is ', num2str(a,'%8.2f'), ' cm2'])
end
function v = volume
v = ar * h;
disp(['Volume of the ingot is ', num2str(v,'%8.2f'), 'cm3'])
end
function w = weight
w = vo * d;
disp(['The weight of ingot is ', num2str(w,'%8.2f'), ' g'])
end
end
运行结果:
>> ingot_calc
Area of circle is 28.27 cm2
Volume of the ingot is 282.74cm3
The weight of ingot is 1272.35 g
Inline 函数(已弃用)
内联函数(inline)已逐步废弃,推荐使用匿名函数(@)。
>> convert_s_to_ms = inline('x*1000','x');
>> convert_s_to_ms(20)
ans = 20000
函数句柄(Function Handles)
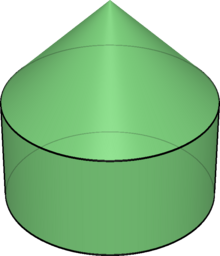 户外嘉年华帐篷
户外嘉年华帐篷

函数句柄(Function handles)是 MATLAB 中的一种双精度数据类型,用于抽象地引用函数。通过函数句柄,可以将一个函数作为参数传递给另一个函数并直接调用计算。匿名函数(Anonymous functions)通常用于命令行求值或在同一个 m 文件中进行多次快速计算。
在 MATLAB 中,使用 @ 符号可以获取一个函数(无论是内置函数还是用户定义的 M 文件函数)的句柄。
示例说明:
我们现在要设计一个嘉年华帐篷,需要计算所需篷布的面积。帐篷由一个圆锥和一个圆柱组合而成:
-
圆锥部分:给定半径 和斜高
-
圆柱部分:给定半径 和高
表面积公式回顾:
-
圆锥侧面积(不含底面):
-
圆柱侧面积 + 顶面积(忽略底面):
其中:
-
:圆锥与圆柱的公共半径
-
:圆锥斜高
-
:圆柱高度
下一步:
按照“在单独文件中创建函数”的步骤,我们将创建一个名为 totalsurftent 的函数,并定义上述两个子函数来分别计算圆锥和圆柱的表面积。
函数句柄是指向函数的引用,可以将函数作为参数传入其他函数。例如:
function [surfcone, surfcylin] = totalsurftent(r, l, h)
% 计算帐篷所需的圆锥和圆柱的表面积
surfcone = sacone(r, l);
surfcylin = sacylin(r, h);
end
function on = sacone(r, l)
on = pi * r * l;
end
function yl = sacylin(r, h)
yl = (2 * pi * r * h) + (pi * r^2);
end
调用:
>> [areacone, areasurfcylin] = totalsurftent(3, 3, 3)
areacone = 28.2743
areasurfcylin = 84.8230
接收函数句柄作为参数的函数
例如:
function result = myfunc(func, a, b)
result = func(a, b);
end
另一个文件中:
function sum = myadd(a, b)
sum = a + b;
end
调用:
>> result = myfunc(@myadd, 1, 2)
result = 3