机器学习
生成训练数据
为了训练我们的学习程序,我们需要一组训练数据,每个数据描述一个特定的棋盘状态 b 及其对应的训练值 Vtrain(b)。每个训练示例都是一个有序对 。
例如,一个训练示例可能是 。这是一个黑色获胜的例子,因为 ,即红色没有剩余棋子。然而,只有对于明确的胜、负或平局棋盘状态 b,才能获得如此清晰的 Vtrain(b) 值。
在上述情况下,对于明确的胜、负或平局棋盘状态 b,分配训练值 Vtrain(b) 是直接的,因为它们属于直接训练经验。但在间接训练经验的情况下,为中间棋盘状态分配训练值 Vtrain(b) 则很困难。在这种情况下,训练值会使用时序差分(Temporal Difference, TD)学习进行更新。时序差分学习是强化学习的核心概念,其中学习通过迭代修正估计的回报,使其更接近准确的目标回报来发生。
让 Successor(b) 表示棋盘状态 b 之后,再次轮到程序走棋的下一个棋盘状态。V^ 是学习器当前对 V 的近似。利用这些信息,将任何中间棋盘状态 b 的训练值 Vtrain(b) 分配如下:
调整权重
现在是时候定义用于选择权重并最适合训练示例集的学习算法了。一种常见的方法是将最佳假设定义为使训练值与假设 V^ 预测值之间的平方误差 E 最小化的假设。
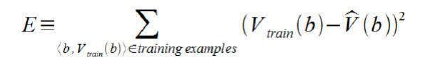
学习算法应该随着更多训练示例的可用性而逐步优化权重,并且需要对训练数据中的错误具有鲁棒性。最小均方(Least Mean Square, LMS)训练规则是一种训练算法,它会小幅调整权重,使其朝着减小误差的方向发展。
LMS 算法定义如下:

Generating training data —
To train our learning program, we need a set of training data, each describing a specific board state b and
the training value V_train (b) for b. Each training example is an ordered pair <b,V_train(b)>
For example, a training example may be <(x1 = 3, x2 = 0, x3 = 1, x4 = 0, x5 = 0, x6 = 0), +100">. This is an
example where black has won the game since x2 = 0 or red has no remaining pieces. However, such clean
values of V_train (b) can be obtained only for board value b that are clear win, loss or draw.
In above case, assigning a training value V_train(b) for the specific boards b that are clean win, loss or
draw is direct as they are direct training experience. But in the case of indirect training experience,
assigning a training value V_train(b) for the intermediate boards is difficult. In such case, the training
values are updated using temporal difference learning. Temporal difference (TD) learning is a concept
central to reinforcement learning, in which learning happens through the iterative correction of your
estimated returns towards a more accurate target return.
Let Successor(b) denotes the next board state following b for which it is again the program’s turn to
move. ^V is the learner’s current approximation to V. Using these information, assign the training value
of V_train(b) for any intermediate board state b as below :
V_train(b) ← ^V(Successor(b))
Adjusting the weights
Now its time to define the learning algorithm for choosing the weights and best fit the set of
training examples. One common approach is to define the best hypothesis as that which minimizes the
squared error E between the training values and the values predicted by the hypothesis ^V.
The learning algorithm should incrementally refine weights as more training examples become available
and it needs to be robust to errors in training data Least Mean Square (LMS) training rule is the one
training algorithm that will adjust weights a small amount in the direction that reduces the error.
The LMS algorithm is defined as follows: