机器学习
在计算机科学中,计算学习理论(或简称学习理论)是人工智能的一个子领域,致力于研究机器学习算法的设计和分析。在计算学习理论中,**概率近似正确学习(PAC 学习)**是机器学习算法数学分析的一个框架。它由 Leslie Valiant 于1984年提出。
在这个框架中,学习器(即算法)接收样本,并且必须从某个假设类别中选择一个假设。目标是以高概率(“概率”部分),所选假设将具有低泛化误差(“近似正确”部分)。在本节中,我们首先给出 PAC 可学习性的非正式定义。在引入更多概念后,我们将给出更正式的、数学导向的 PAC 可学习性定义。最后,我们将提及 PAC 可学习性的一个应用。
PAC 可学习性
为了定义 PAC 可学习性,我们需要一些特定的术语和相关符号。
-
设 X 是一个称为实例空间的集合,它可以是有限的或无限的。 例如,X 可以是平面上所有点的集合。
-
X 的概念类 C 是函数 的族。 C 的一个成员称为一个概念。一个概念也可以被认为是 X 的一个子集。如果 C 是 X 的一个子集,它定义了一个唯一的函数 ,如下所示:
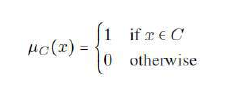
-
假设 h 也是一个函数 。 因此,与概念的情况一样,假设也可以被认为是 X 的一个子集。H 将表示一个假设集。
-
我们假设 F 是 X 上的一个任意但固定的概率分布。
-
训练示例是通过从 X 中随机抽样获得的。 我们假设样本是根据概率分布 F 从 X 中随机生成的。
现在,我们给出 PAC 可学习性的非正式定义。
定义(非正式)
设 X 是一个实例空间,C 是 X 的一个概念类,h 是 C 中的一个假设,F 是一个任意但固定的概率分布。如果存在一个算法 A,对于以任何概率分布 F 和任何概念 抽取的样本,它将以高概率产生一个误差小的假设 ,则称概念类 C 是 PAC 可学习的。
示例
为了说明 PAC 可学习性的定义,让我们考虑一些具体示例。
示例
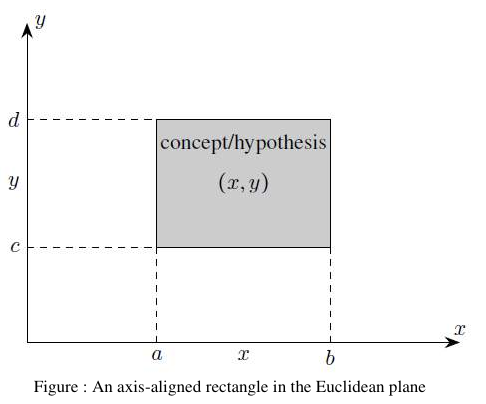
图:欧几里得平面上的轴对齐矩形
- 设实例空间为欧几里得平面中所有点的集合 X。 每个点由其坐标 (x,y) 表示。因此,实例的维度或长度为 2。
- 设概念类 C 为平面中所有“轴对齐矩形”的集合;也就是说,其边与平面中坐标轴平行的所有矩形的集合(见图)。
- 由于轴对齐矩形可以由以下形式的一组不等式定义,该不等式有四个参数:
- 概念的大小为 4。
- 我们将所有假设的集合 H 等同于概念的集合 C,即 。
给定一组标记为正或负的样本点,设 L 是一个算法,它输出由对正例进行最紧密拟合的轴对齐矩形定义的假设(即包含所有正例且不包含任何负例的最小面积矩形)(见下图)。
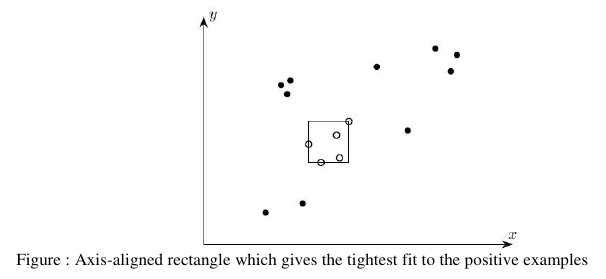
图:对正例进行最紧密拟合的轴对齐矩形
可以证明,在上面引入的符号中,概念类 C 可以通过算法 L 使用所有轴对齐矩形的假设空间 H 进行 PAC 可学习。
In computer science, computational learning theory (or just learning theory) is a subfield of
artificial intelligence devoted to studying the design and analysis of machine learning algorithms. In
computational learning theory, probably approximately correct learning (PAC learning) is a framework
for mathematical analysis of machine learning algorithms. It was proposed in 1984 by Leslie Valiant.
In this framework, the learner (that is, the algorithm) receives samples and must select a
hypothesis from a certain class of hypotheses. The goal is that, with high probability (the “probably”
part), the selected hypothesis will have low generalization error (the “approximately correct” part). In
this section we first give an informal definition of PAC-learnability. After introducing a few nore notions,
we give a more formal, mathematically oriented, definition of PAC-learnability. At the end, we mention
one of the applications of PAC-learnability.
PAC-learnability
To define PAC-learnability we require some specific terminology and related notations.
Let X be a set called the instance space which may be finite or infinite. For example, X may be
the set of all points in a plane.
A concept class C for X is a family of functions c : X {0; 1}. A member of C is called a concept.
A concept can also be thought of as a subset of X. If C is a subset of X, it defines a unique
function μc : X {0; 1} as follows:
A hypothesis h is also a function h : X {0; 1}. So, as in the case of concepts, a hypothesis can
also be thought of as a subset of X. H will denote a set of hypotheses.
We assume that F is an arbitrary, but fixed, probability distribution over X.
Training examples are obtained by taking random samples from X. We assume that the samples
are randomly generated from X according to the probability distribution F.
Now, we give below an informal definition of PAC-learnability.
Definition (informal)
Let X be an instance space, C a concept class for X, h a hypothesis in C and F an arbitrary, but fixed,
probability distribution. The concept class C is said to be PAC-learnable if there is an algorithm A which,
for samples drawn with any probability distribution F and any concept c Є C, will with high probability
produce a hypothesis h Є C whose error is small.
Examples
To illustrate the definition of PAC-learnability, let us consider some concrete examples .
Example
Figure : An axis-aligned rectangle in the Euclidean plane
21
Let the instance space be the set X of all points in the Euclidean plane. Each point is represented
by its coordinates (x; y). So, the dimension or length of the instances is 2.
Let the concept class C be the set of all “axis-aligned rectangles” in the plane; that is, the set of
all rectangles whose sides are parallel to the coordinate axes in the plane (see Figure).
Since an axis-aligned rectangle can be defined by a set of inequalities of the following form
having four parameters
a ≤ x ≤ b, c ≤ y ≤ d
the size of a concept is 4.
We take the set H of all hypotheses to be equal to the set C of concepts, H = C.
Given a set of sample points labeled positive or negative, let L be the algorithm which outputs the
hypothesis defined by the axis-aligned rectangle which gives the tightest fit to the positive examples
(that is, that rectangle with the smallest area that includes all of the positive examples and none of the
negative examples) (see Figure bleow).
Figure : Axis-aligned rectangle which gives the tightest fit to the positive examples
It can be shown that, in the notations introduced above, the concept class C is PAC-learnable by the
algorithm L using the hypothesis space H of all axis-aligned rectangles.