机器学习
ID3 算法将递归执行以下任务:
- 创建树的根节点。
- 如果所有示例都是正例,返回叶节点“positive”。
- 否则,如果所有示例都是负例,返回叶节点“negative”。
- 计算当前状态的熵 H(S)。
- 对于每个属性,计算相对于属性“x”的熵,记为 H(S,x)。
- 选择具有最大 IG(S,x) 值的属性。
- 从属性集中移除提供最高信息增益的属性。
- 重复此过程,直到所有属性都用完,或者决策树的所有节点都是叶节点。
现在我们开始构建决策树。第一步是计算当前状态的熵 H(S)。
在上面的例子中,我们可以看到总共有 5 个“否”和 9 个“是”。
| 是 | 否 | 总计 |
| 9 | 5 | 14 |
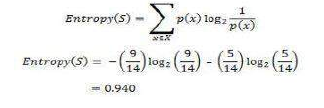
其中“x”是属性的可能值。在这里,属性“Wind”(风)在样本数据中取两个可能的值,因此 ,我们必须计算:

在所有 14 个示例中,我们有 8 个风力“弱”的例子和 6 个风力“强”的例子。
| 风力 = 弱 | 风力 = 强 | 总计 |
| 8 | 6 | 14 |
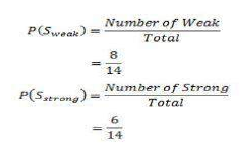
现在,在 8 个风力“弱”的例子中,有 6 个“Play Golf”(打高尔夫)是“是”,2 个“Play Golf”是“否”。所以我们有:
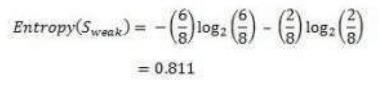
类似地,在 6 个风力“强”的例子中,我们有 3 个“Play Golf”是“是”,3 个“Play Golf”是“否”。
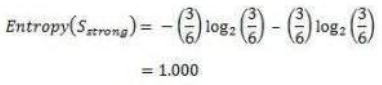
请记住,这里一半项目属于一个类别,另一半属于另一个类别。因此我们具有完美的随机性。
现在我们拥有计算信息增益所需的所有要素:
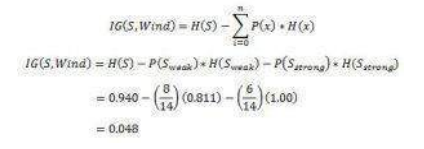
它告诉我们考虑“Wind”作为特征所获得的信息增益为 0.048。
现在我们必须类似地计算所有特征的信息增益。
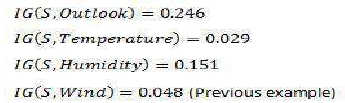
我们可以清楚地看到,IG(S,Outlook) 具有最高的信息增益 0.246,因此我们选择 Outlook 属性作为根节点。此时,决策树看起来像这样:
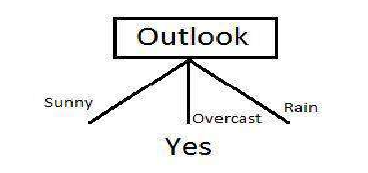
在这里我们观察到,每当 Outlook(天气)是“Overcast”(阴天)时,“Play Golf”总是“Yes”(是),这并非巧合,简单树之所以形成,是因为 Outlook 属性提供了最高的信息增益。现在我们如何从这一点继续?我们可以简单地应用递归,您可能想看看前面描述的算法步骤。现在我们已经使用了 Outlook,还剩下 Humidity(湿度)、Temperature(温度)和 Wind(风)三个。并且,Outlook 有三个可能的值:Sunny(晴朗)、Overcast(阴天)、Rain(下雨)。其中 Overcast 节点已经是一个叶节点“Yes”,所以我们剩下两个子树需要计算:Sunny 和 Rain。
![]()
Outlook 值为 Sunny 的表格如下所示:
| Temperature | Humidity | Wind | Play Golf |
| Hot | High | Weak | No |
| Hot | High | Strong | No |
| Mild | High | Weak | No |
| Cool | Normal | Weak | Yes |
| Mild | Normal | Strong | Yes |
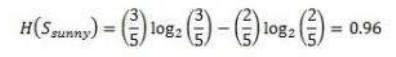
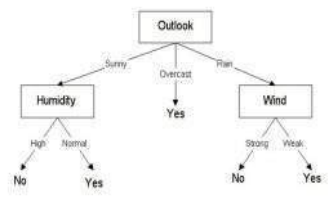
我们可以看到,最高的信息增益是由 Humidity(湿度)提供的。以同样的方式继续![]() ,Wind(风)将是信息增益最高的属性。最终的决策树看起来像这样。最终的决策树看起来像这样。
,Wind(风)将是信息增益最高的属性。最终的决策树看起来像这样。最终的决策树看起来像这样。
ID3 Algorithm will perform following tasks recursively
1.
2.
3.
4.
5.
6.
7.
8.
Create root node for the tree
If all examples are positive, return leaf node „positive‟
Else if all examples are negative, return leaf node „negative‟
Calculate the entropy of current state H(S)
For each attribute, calculate the entropy with respect to the attribute „x‟ denoted by H(S, x)
Select the attribute which has maximum value of IG(S, x)
Remove the attribute that offers highest IG from the set of attributes
Repeat until we run out of all attributes, or the decision tree has all leaf nodes.
Now we‟ll go ahead and grow the decision tree. The initial step is to calculate H(S), the Entropy of the current state.
In the above example, we can see in total there are 5 No‟s and 9 Yes‟s.
Yes
No
Total
9
5
14
where „x‟ are the possible values for an attribute. Here, attribute „Wind‟ takes two possible values in the sample
data, hence x = {Weak, Strong} we‟ll have to calculate:
Amongst all the 14 examples we have 8 places where the wind is weak and 6 where the wind is Strong.
Wind = Weak
Wind = Strong
Total
8
6
14
Now out of the 8 Weak examples, 6 of them were „Yes‟ for Play Golf and 2 of them were „No‟ for „Play Golf‟. So,
we have,
Similarly, out of 6 Strong examples, we have 3 examples where the outcome was „Yes‟ for Play Golf and 3
where we had „No‟ for Play Golf.
Remember, here half items belong to one class while other half belong to other. Hence we have perfect randomness.
Now we have all the pieces required to calculate the Information Gain,
Which tells us the Information Gain by considering „Wind‟ as the feature and give us information gain of 0.048.
Now we must similarly calculate the Information Gain for all the features.
We can clearly see that IG(S, Outlook) has the highest information gain of 0.246, hence we chose Outlook
attribute as the root node. At this point, the decision tree looks like.
27
Here we observe that whenever the outlook is Overcast, Play Golf is always ‘Yes’, it’s no coincidence by
any chance, the simple tree resulted because of the highest information gain is given by the attribute
Outlook. Now how do we proceed from this point? We can simply apply recursion, you might want to
look at the algorithm steps described earlier. Now that we’ve used Outlook, we’ve got three of them
remaining Humidity, Temperature, and Wind. And, we had three possible values of Outlook: Sunny,
Overcast, Rain. Where the Overcast node already ended up having leaf node ‘Yes’, so we’re left with
two subtrees to compute: Sunny and Rain.
Table where the value of Outlook is Sunny looks like:
Temperature
Humidity
Wind
Play Golf
Hot
High
Weak
No
Hot
High
Strong
No
Mild
High
Weak
No
Cool
Normal
Weak
Yes
Mild
Normal
Strong
Yes
As we can see the highest Information Gain is given by Humidity. Proceeding in the same way with
will give us Wind as the one with highest information gain. The final Decision Tree looks something like
this. The final Decision Tree looks something like this.