机器学习
-
线性回归是一种用于预测分析的统计回归方法。
-
它是非常简单易懂的算法之一,适用于回归问题并显示连续变量之间的关系。
-
它用于解决机器学习中的回归问题。
-
线性回归显示自变量(X轴)与因变量(Y轴)之间的线性关系,因此被称为线性回归。
-
如果只有一个输入变量(X),则这种线性回归称为简单线性回归。如果有一个以上的输入变量,则这种线性回归称为多元线性回归。
-
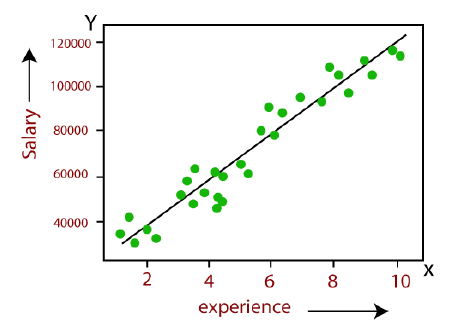
线性回归模型中变量之间的关系可以用下图解释。
在这里,我们根据员工的工作经验年限来预测其薪资。
以下是线性回归的数学方程:
Y=aX+b
其中:
- Y = 因变量(目标变量)
- X = 自变量(预测变量)
- a 和 b 是线性系数
线性回归的一些流行应用包括:
- 分析趋势和销售预测
- 薪资预测
- 房地产预测
- 计算交通中的预计到达时间(ETA)
o Linear regression is a statistical regression method which is used for predictive analysis.
o It is one of the very simple and easy algorithms which works on regression and shows the relationship
between the continuous variables.
o It is used for solving the regression problem in machine learning.
o Linear regression shows the linear relationship between the independent variable (X-axis) and the
dependent variable (Y-axis), hence called linear regression.
o
o
If there is only one input variable (x), then such linear regression is called simple linear regression. And if
there is more than one input variable, then such linear regression is called multiple linear regression.
The relationship between variables in the linear regression model can be explained using the below image.
Here we are predicting the salary of an employee on the basis of the year of experience.
Below is the mathematical equation for Linear regression:
Y= aX+b
Here, Y = dependent variables (target variables),
X= Independent variables (predictor variables),
a and b are the linear coefficients
Some popular applications of linear regression are:
o Analyzing trends and sales estimates
o
Salary forecasting
o
Real estate prediction
o
Arriving at ETAs in traffic.