机器学习
多层感知器(MLP) 是一种监督学习算法,它通过在数据集上训练来学习一个函数 ,其中 m 是输入的维度, o 是输出的维度。给定一组特征 和一个目标 y,它可以学习一个用于分类或回归的非线性函数逼近器。它与逻辑回归不同之处在于,在输入层和输出层之间,可以有一个或多个非线性层,称为隐藏层。下图显示了一个带有一个标量输出的单隐藏层 MLP。
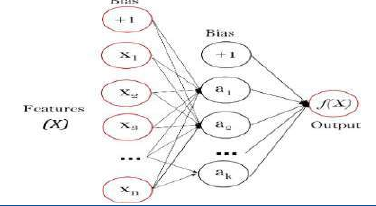
最左边的层,称为输入层,由一组神经元 {xi∣x1,x2,...,xm} 组成,代表输入特征。隐藏层中的每个神经元将前一层的值进行加权线性求和 ,然后通过一个非线性激活函数 (例如双曲正切函数)进行转换。输出层接收来自最后一个隐藏层的值,并将其转换为输出值。
该模块包含公共属性 coefs_ 和 intercepts_。coefs_ 是一个权重矩阵列表,其中索引 i 处的权重矩阵表示层 i 和层 之间的权重。intercepts_ 是一个偏置向量列表,其中索引 i 处的向量表示添加到层 的偏置值。
多层感知器的优点是:
- 能够学习非线性模型。
- 能够使用
partial_fit进行实时学习(在线学习)。
多层感知器(MLP)的缺点包括:
- 具有隐藏层的 MLP 具有非凸损失函数,其中存在多个局部最小值。因此,不同的随机权重初始化可能导致不同的验证准确性。
- MLP 需要调整多个超参数,例如隐藏神经元的数量、层数和迭代次数。
- MLP 对特征缩放敏感。
Multi-layer Perceptron (MLP) is a supervised learning algorithm that learns a
function f(⋅):Rm→Ro by training on a dataset, where m is the number of dimensions for input and o is the
number of dimensions for output. Given a set of features X=x1 ,x2,...,xm and a target y, it can learn a non-
linear function approximator for either classification or regression. It is different from logistic
regression, in that between the input and the output layer, there can be one or more non-linear layers,
called hidden layers. Figure shows a one hidden layer MLP with scalar output.
The leftmost layer, known as the input layer, consists of a set of neurons {xi|x 1,x2,...,xm} representing the
input features. Each neuron in the hidden layer transforms the values from the previous layer with a
weighted linear summation w1x1+w2x 2+...+wmxm, followed by a non-linear activation function g(⋅):R→R -
like the hyperbolic tan function. The output layer receives the values from the last hidden layer and
transforms them into output values.
The module contains the public attributes coefs_ and intercepts_. coefs_ is a list of weight matrices,
where weight matrix at index i represents the weights between layer i and layer i+1. intercepts_ is a list
of bias vectors, where the vector at index i represents the bias values added to layer i+1.
The advantages of Multi-layer Perceptron are:
Capability to learn non-linear models.
Capability to learn models in real-time (on-line learning) using partial_fit.
The disadvantages of Multi-layer Perceptron (MLP) include:
MLP with hidden layers have a non-convex loss function where there exists more than one local
minimum. Therefore different random weight initializations can lead to different validation
accuracy.
MLP requires tuning a number of hyperparameters such as the number of hidden neurons,
layers, and iterations.
MLP is sensitive to feature scaling.