机器学习
支持向量机(SVM) 是最受欢迎的监督学习算法之一,它既可用于分类问题,也可用于回归问题。然而,它主要应用于机器学习中的分类问题。SVM 算法的目标是创建最佳直线或决策边界,该边界能够将 n 维空间划分为不同的类别,以便我们将来能轻松地将新数据点放入正确的类别。这个最佳决策边界称为超平面。
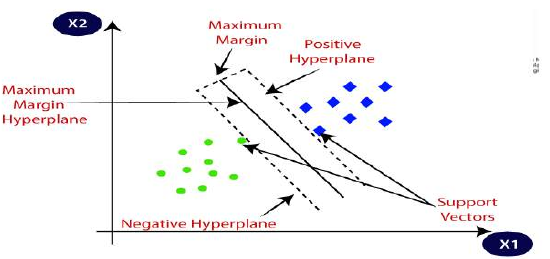
SVM 会选择有助于创建超平面的极端点/向量。这些极端案例被称为支持向量,因此该算法被称为支持向量机。请看下图,其中两个不同的类别通过决策边界或超平面进行分类:
示例:我们可以用 KNN 分类器中使用过的例子来理解 SVM。假设我们看到一只既有猫的特征也有狗的特征的奇怪动物,如果我们想创建一个模型来准确识别它是猫还是狗,那么就可以使用 SVM 算法来创建这样的模型。我们将首先用大量的猫和狗的图片训练我们的模型,以便它能够学习猫和狗的不同特征,然后用这个奇怪的生物来测试它。由于支持向量会在猫和狗这两个数据之间创建一个决策边界,并选择极端案例(支持向量),它会观察猫和狗的极端案例。根据支持向量,它会将其分类为猫。请看下图:
SVM 算法可用于人脸识别、图像分类、文本分类等。
SVM 的类型
SVM 可以分为两种类型:
- 线性 SVM:线性 SVM 用于线性可分数据,这意味着如果一个数据集可以使用一条直线分成两类,那么这种数据被称为线性可分数据,使用的分类器被称为线性 SVM 分类器。
- 非线性 SVM:非线性 SVM 用于非线性可分数据,这意味着如果一个数据集不能用一条直线进行分类,那么这种数据被称为非线性数据,使用的分类器被称为非线性 SVM 分类器。
SVM 算法中的超平面和支持向量:
-
超平面:在 n 维空间中可以有多条线/决策边界来分隔类别,但我们需要找出有助于分类数据点的最佳决策边界。这个最佳边界被称为 SVM 的超平面。
超平面的维度取决于数据集中存在的特征数量,这意味着如果有 2 个特征(如图片所示),则超平面将是一条直线。如果有 3 个特征,则超平面将是一个 2 维平面。
我们总是创建一个具有最大间隔的超平面,这意味着数据点之间的距离最大。
-
支持向量:
最接近超平面并影响超平面位置的数据点或向量被称为支持向量。由于这些向量支持超平面,因此被称为支持向量。SVM 是如何工作的?
Support Vector Machine or SVM is one of the most popular Supervised Learning algorithms,
which is used for Classification as well as Regression problems. However, primarily, it is used for
Classification problems in Machine Learning. The goal of the SVM algorithm is to create the best line or
decision boundary that can segregate n-dimensional space into classes so that we can easily put the
new data point in the correct category in the future. This best decision boundary is called a hyperplane.
SVM chooses the extreme points/vectors that help in creating the hyperplane. These extreme cases are
called as support vectors, and hence algorithm is termed as Support Vector Machine. Consider the
below diagram in which there are two different categories that are classified using a decision boundary
or hyperplane:
Example: SVM can be understood with the example that we have used in the KNN classifier. Suppose
we see a strange cat that also has some features of dogs, so if we want a model that can accurately
identify whether it is a cat or dog, so such a model can be created by using the SVM algorithm. We will
first train our model with lots of images of cats and dogs so that it can learn about different features of
cats and dogs, and then we test it with this strange creature. So as support vector creates a decision
boundary between these two data (cat and dog) and choose extreme cases (support vectors), it will see
the extreme case of cat and dog. On the basis of the support vectors, it will classify it as a cat. Consider
the below diagram:
SVM algorithm can be used for Face detection, image classification, text categorization, etc.
Types of SVM
SVM can be of two types:
o
Linear SVM: Linear SVM is used for linearly separable data, which means if a dataset can be
classified into two classes by using a single straight line, then such data is termed as linearly
separable data, and classifier is used called as Linear SVM classifier.
o
Non-linear SVM: Non-Linear SVM is used for non-linearly separated data, which means if a
dataset cannot be classified by using a straight line, then such data is termed as non-linear data
and classifier used is called as Non-linear SVM classifier.
Hyperplane and Support Vectors in the SVM algorithm:
Hyperplane: There can be multiple lines/decision boundaries to segregate the classes in n-
dimensional space, but we need to find out the best decision boundary that helps to classify the data
points. This best boundary is known as the hyperplane of SVM.
The dimensions of the hyperplane depend on the features present in the dataset, which means if there
are 2 features (as shown in image), then hyperplane will be a straight line. And if there are 3 features,
then hyperplane will be a 2-dimension plane.
We always create a hyperplane that has a maximum margin, which means the maximum distance
between the data points.
Support Vectors:
The data points or vectors that are the closest to the hyperplane and which affect the position of the
hyperplane are termed as Support Vector. Since these vectors support the hyperplane, hence called a
Support vector. How does SVM works?