机器学习
我们可以通过一个例子来理解 SVM 算法的工作原理。假设我们有一个数据集,它有两个标签(绿色和蓝色),并且数据集有两个特征 x1 和 x2。我们想要一个分类器,能够将坐标对 (x1,x2) 分类为绿色或蓝色。请看下图:
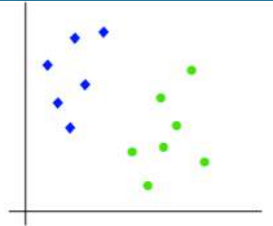
由于这是一个二维空间,我们只需使用一条直线就可以轻松地将这两个类别分开。但是,可能有多条直线可以分隔这些类别。请看下图:
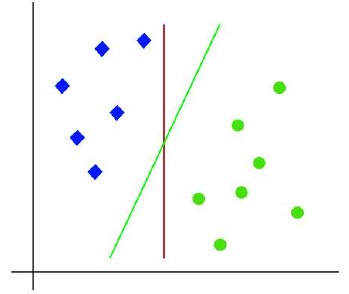
因此,SVM 算法帮助我们找到最佳直线或决策边界;这个最佳边界或区域被称为超平面。SVM 算法找到距离这条直线最近的来自两个类别的点。这些点被称为支持向量。支持向量与超平面之间的距离被称为间隔。SVM 的目标就是最大化这个间隔。具有最大间隔的超平面被称为最优超平面。
The working of the SVM algorithm can be understood by using an example. Suppose we have a dataset
that has two tags (green and blue), and the dataset has two features x1 and x2. We want a classifier
that can classify the pair(x1, x2) of coordinates in either green or blue. Consider the below image:
So as it is 2-d space so by just using a straight line, we can easily separate these two classes. But there
can be multiple lines that can separate these classes. Consider the below image:
Hence, the SVM algorithm helps to find the best line or decision boundary; this best boundary or region
is called as a hyperplane. SVM algorithm finds the closest point of the lines from both the classes. These
points are called support vectors. The distance between the vectors and the hyperplane is called
as margin. And the goal of SVM is to maximize this margin. The hyperplane with maximum margin is
called the optimal hyperplane.