机器学习
堆叠泛化 (Stacked generalization) 是 Wolpert (1992) 提出的一种技术,它扩展了投票法的概念。与投票法不同的是,基学习器输出的组合方式不一定局限于线性组合,而是通过一个组合器系统 f(⋅∣Φ) 来学习。这个组合器本身也是一个学习器,其参数 Φ 同样需要训练。(请看下图)
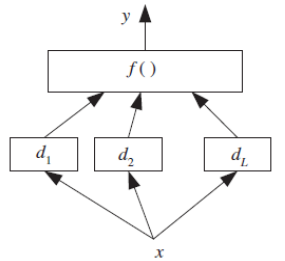
图:在堆叠泛化中,组合器是另一个学习器,并不像投票法那样局限于线性组合。
组合器学习的是当基学习器给出某种输出组合时,正确的输出应该是什么。我们不能在训练数据上训练组合函数,因为基学习器可能已经记住了训练集;实际上,组合器系统应该学习基学习器是如何犯错误的。堆叠泛化是一种估计并纠正基学习器偏差的方法。因此,组合器应该在训练基学习器时未曾使用过的数据上进行训练。
如果 f(⋅∣w1,...,wL) 是一个带有约束 的线性模型,那么最优权重可以通过约束回归找到。但当然,我们不需要强制执行这些约束;在堆叠泛化中,对组合函数没有限制,与投票法不同,f(⋅) 可以是非线性的。例如,它可以实现为具有其连接权重 Φ 的多层感知器。
基学习器 dj 的输出定义了一个新的 L 维空间,在这个空间中,输出判别/回归函数由组合函数学习。
在堆叠泛化中,我们希望基学习器尽可能不同,以便它们能够相互补充。为此,最好是它们基于不同的学习算法。如果我们将能够生成连续输出(例如后验概率)的分类器进行组合,那么最好是组合它们而不是硬性决策。
当我们比较堆叠泛化中的经过训练的组合器与投票法中固定的规则时,我们发现两者各有优势:训练过的规则更灵活,并且可能具有更小的偏差,但它增加了额外的参数,有引入方差的风险,并且需要额外的训练时间和数据。另外请注意,在堆叠之前无需对分类器输出进行归一化。
3.5.2 Stacking - Stacked Generalization
Stacked generalization is a technique proposed by Wolpert (1992) that extends voting in that
the way the output of the base-learners is combined need not be linear but is learned through a
combiner system, f (·|Φ), which is another learner, whose parameters Φ are also trained. (see the
below given figure)
Figure: In stacked generalization, the combiner is another learner and is not restricted to being a linear
combination as in voting.
y = f (d1, d2, . . . , dL |Φ)
The combiner learns what the correct output is when the base-learners give a certain output
combination. We cannot train the combiner function on the training data because the base-learners
may be memorizing the training set; the combiner system should actually learn how the baselearners
make errors. Stacking is a means of estimating and correcting for the biases of the base-learners.
Therefore, the combiner should be trained on data unused in training the base-learners.
If f (·|w1, . . . , wL) is a linear model with constraints, wi ≥ 0, jWj = 1, the optimal weights can be found
by constrained regression, but of course we do not need to enforce this; in stacking, there is no
restriction on the combiner function and unlike voting, f (·) can be nonlinear. For example, it may be
implemented as a multilayer perceptron with Φ its connection weights.
The outputs of the base-learners dj define a new L-dimensional space in which the output
discriminant/regression function is learned by the combiner function.
In stacked generalization, we would like the base-learners to be as different as possible so that they will
complement each other, and, for this, it is best if they are based on different learning algorithms. If we
are combining classifiers that can generate continuous outputs, for example, posterior probabilities, it is
better that they be the combined rather than hard decisions.
When we compare a trained combiner as we have in stacking, with a fixed rule such as in
voting, we see that both have their advantages: A trained rule is more flexible and may have less bias,
but adds extra parameters, risks introducing variance, and needs extra time and data for training. Note
also that there is no need to normalize classifier outputs before stacking.