机器学习
遗传算法 (GAS) 可以被视为一种通用的优化方法,它在庞大的候选对象空间中搜索,以期找到一个根据适应度函数表现最佳的对象。虽然不能保证找到最优对象,但 GAS 通常能成功找到具有高适应度的对象。遗传算法已应用于机器学习之外的许多优化问题,包括电路布局和作业车间调度等问题。在机器学习领域,它们已被应用于函数逼近问题以及为人工神经网络学习系统选择网络拓扑等任务。
为了说明遗传算法在概念学习中的应用,我们简要总结由 DeJong 等人 (1993) 描述的 GABIL 系统。GABIL 使用遗传算法来学习由命题规则的析取集表示的布尔概念。在针对多个概念学习问题进行的实验中,GABIL 在泛化准确性方面被发现与决策树学习算法 C4.5 和规则学习系统 AQ14 等其他学习算法大致相当。本研究中的学习任务既包括旨在探索系统泛化准确性的人工学习任务,也包括乳腺癌诊断的真实世界问题。
GABIL 中遗传算法的具体实现可以总结如下:
表示方法:GABIL 中的每个假设都对应于一个命题规则的析取集,按照 9.2.1 节中的描述进行编码。具体来说,规则前置条件的假设空间是由固定属性集上的约束的合取组成,如前面章节所述。为了表示一组规则,单个规则的位串表示被连接起来。为了说明,考虑一个假设空间,其中规则前置条件是对两个布尔属性 a1 和 a2 的约束合取。规则后置条件由一个表示目标属性 c 的预测值的单一位描述。因此,由以下两条规则组成的假设:
![]()
如果 a1=T ∧ a2=F 则 c=T;如果 a2=T 则 c=F
将由以下字符串表示:
| a1 | a2 | c |
| 10 | 01 | 1 |
| a1 | a2 | c |
| 11 | 01 | 0 |
请注意,位串的长度随着假设中规则数量的增加而增长。这种可变位串长度需要对交叉操作符进行轻微修改,如下所述。
遗传操作符:GABIL 使用上表中标准的变异操作符,其中随机选择一个位并替换为其补码。它使用的交叉操作符是表 9.2 中描述的两点交叉操作符的相当标准的扩展。特别是,为了适应编码规则集的可变长度位串,并限制系统使交叉仅发生在编码规则的位串的同类部分之间,采取了以下方法:对两个父代进行交叉操作时,首先在第一个父代字符串中随机选择两个交叉点。设 d1 (d2) 表示这两个交叉点中最左侧(最右侧)的交叉点到其左侧紧邻的规则边界的距离。现在在第二个父代中随机选择交叉点,但受限于它们必须具有相同的 d1 和 d2 值。例如,如果两个父代字符串是:
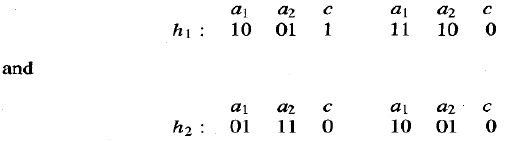
并且为第一个父代选择的交叉点是位位置 1 和 8 之后的点,
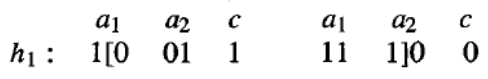
其中 "[" 和 "]" 表示交叉点,那么 和 。因此,第二个父代允许的交叉点对包括位位置 (1,3)、(1,8) 和 (6,8)。如果恰好选择了 (1,3) 对,则生成的两个子代将是:

正如这个例子所示,这种交叉操作使得子代可以包含与父代不同数量的规则,同时确保以这种方式生成的所有位串都表示定义明确的规则集。
适应度函数:每个假设规则集的适应度都基于其在训练数据上的分类准确性。具体来说,用于衡量适应度的函数是:
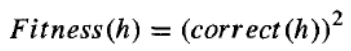
其中 correct(h) 是假设 h 正确分类的所有训练样本的百分比。
在将 GABIL 的行为与决策树学习算法(如 C4.5 和 ID5R)以及规则学习算法 AQ14 进行比较的实验中,报告称这些系统在各种学习问题上表现大致相当。例如,在一组 12 个合成问题上,GABIL 实现了 92.1% 的平均泛化准确性,而其他系统的表现范围从 91.2% 到 96.6%。
扩展
在一组实验中,他们探索了增加两种新的遗传操作符,这些操作符受到了许多符号学习方法中常见的泛化操作符的启发。第一个操作符 AddAlternative 通过将对应于该属性的子串中的 0 更改为 1 来泛化对特定属性的约束。例如,如果对某个属性的约束由字符串 10010 表示,则此操作符可能会将其更改为 10110。此操作符在每代中以 0.01 的概率应用于种群中选定的成员。第二个操作符 Dropcondition 执行更彻底的泛化步骤,通过将特定属性的所有位替换为 1。此操作符对应于通过完全删除对该属性的约束来泛化规则,并在每代中以 0.60 的概率应用。作者报告称,这个修订后的系统在上述合成学习任务集上的平均性能达到了 95.2%,而基本遗传算法为 92.1%。
在上述实验中,这两个新操作符在每代中以相同的概率应用于种群中的每个假设。在第二个实验中,假设的位串表示被扩展,以包含两个位,用于确定哪些操作符可以应用于该假设。在这种扩展表示中,典型规则集假设的位串将是:
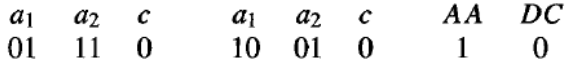
其中最后两位在这种情况下表示 AddAlternative 操作符可以应用于此位串,但 Dropcondition 操作符不能。这两个新位定义了遗传算法使用的搜索策略的一部分,它们本身也使用作用于字符串中其他位的相同交叉和变异操作符进行改变和进化。虽然作者报告了这种方法的混合结果(即,在某些问题上性能有所提高,在另一些问题上性能有所下降),但它提供了一个有趣的例子,说明遗传算法原则上可以如何用于进化自己的假设搜索方法。
A genetic algorithm can be viewed as a general optimization method that searches a large space
of candidate objects seeking one that performs best according to the fitness function. Although not
guaranteed to find an optimal object, GAS often succeed in finding an object with high fitness. GAS have
been applied to a number of optimization problems outside machine learning, including problems such
as circuit layout and job-shop scheduling. Within machine learning, they have been applied both to
function-approximation problems and to tasks such as choosing the network topology for artificial
neural network learning systems.
To illustrate the use of GAS for concept learning, we briefly summarize the GABIL system
described by DeJong et al. (1993). GABIL uses a GA to learn boolean concepts represented by a
disjunctive set of propositional rules. In experiments over several concept learning problems, GABIL was
found to be roughly comparable in generalization accuracy to other learning algorithms such as the
decision tree learning algorithm C4.5 and the rule learning system AQ14. The learning tasks in this study
included both artificial learning tasks designed to explore the systems' generalization accuracy and the
real world problem of breast cancer diagnosis.
The specific instantiation of the GA algorithm in GABIL can be summarized as follows:
Representation. Each hypothesis in GABIL corresponds to a disjunctive set of propositional rules,
encoded as described in Section 9.2.1. In particular, the hypothesis space of rule preconditions consists
of a conjunction of constraints on a fixed set of attributes, as described in that earlier section. To
represent a set of rules, the bit-string representations of individual rules are concatenated. To illustrate,
consider a hypothesis space in which rule preconditions are conjunctions of constraints over two
Boolean attributes, a1 and a2.The rule postcondition is described by a single bit that indicates the
predicted value of the target attribute c. Thus, the hypothesis consisting of the two rules
IF al=T^a2=F THEN c=T; IF a2=T THEN c=F
would be represented by the string
a1 a2 c
10 01 1
a1 a2 c
11 01 0
Note the length of the bit string grows with the number of rules in the hypothesis. This variable bit-
string length requires a slight modification to the crossover operator, as described below.
Genetic operators. GABIL uses the standard mutation operator of above Table in which a single
bit is chosen at random and replaced by its complement. The crossover operator that it uses is a fairly
standard extension to the two-point crossover operator described in Table 9.2. In particular, to
accommodate the variable-length bit strings that encode rule sets, and to constrain the system so that
crossover occurs only between like sections of the bit strings that encode rules, the following approach
is taken. To perform a crossover operation on two parents, two crossover points are first chosen at
random in the first parent string. Let dl (dz) denote the distance from the leftmost (rightmost) of these
two crossover points to the rule boundary immediately to its left. The crossover points in the second
parent are now randomly chosen, subject to the constraint that they must have the same dl and d2
value. For example, if the two parent strings are
and the crossover points chosen for the first parent are the points following bit positions 1 and 8,
where "[" and "1" indicate crossover points, then dl = 1 and dz = 3. Hence the allowed pairs of crossover
points for the second parent include the pairs of bit positions (1,3), (1,8), and (6,8). If the pair (1,3)
happens to be chosen,
then the two resulting offspring will be
As this example illustrates, this crossover operation enables offspring to contain a different number of
rules than their parents, while assuring that all bit strings generated in this fashion represent well-
defined rule sets.
Fitness function. The fitness of each hypothesized rule set is based on its classification accuracy over
the training data. In particular, the function used to measure fitness is
where correct is the percent of all training examples correctly classified by hypothesis h.
In experiments comparing the behavior of GABIL to decision tree learning algorithms such as
C4.5 and ID5R, and to the rule learning algorithm AQ14report roughly comparable performance among
these systems, tested on a variety of learning problems. For example, over a set of 12 synthetic
problems, GABIL achieved an average generalization accuracy of 92.1 %, whereas the performance of
the other systems ranged from 91.2 % to 96.6 %.
Extensions
106
In one set of experiments they explored the addition of two new genetic operators that were
motivated by the generalization operators common in many symbolic learning methods. The first of
these operators, AddAlternative, generalizes the constraint on a specific attribute by changing a 0 to a
1 in the substring corresponding to the attribute. For example, if the constraint on an attribute is
represented by the string 10010, this operator might change it to 101 10. This operator was applied
with probability .O1 to selected members of the population on each generation. The second operator,
Dropcondition performs a more drastic generalization step, by replacing all bits for a particular attribute
by a 1. This operator corresponds to generalizing the rule by completely dropping the constraint on the
attribute, and was applied on each generation with probability .60. The authors report this revised
system achieved an average performance of 95.2% over the above set of synthetic learning tasks,
compared to 92.1% for the basic GA algorithm.
In the above experiment, the two new operators were applied with the same probability to each
hypothesis in the population on each generation. In a second experiment, the bit-string representation
for hypotheses was extended to include two bits that determine which of these operators may be
applied to the hypothesis. In this extended representation, the bit string for a typical rule set hypothesis
would be
where the final two bits indicate in this case that the AddAlternative operator may be applied to this bit
string, but that the Dropcondition operator may not. These two new bits define part of the search
strategy used by the GA and are themselves altered and evolved using the same crossover and mutation
operators that operate on other bits in the string. While the authors report mixed results with this
approach (i.e., improved performance on some problems, decreased performance on others), it
provides an interesting illustration of how GAS might in principle be used to evolve their own
hypothesis search methods.