机器学习
遗传编程 (GP) 是一种进化计算形式,其中进化种群中的个体是计算机程序,而不是位串。基本的遗传编程方法展现了可以通过 GP 成功学习的各种简单程序。
程序表示
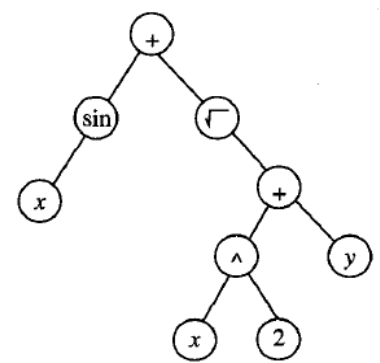
GP 操作的程序通常由对应于程序语法树的树来表示。每个函数调用都由树中的一个节点表示,函数的参数由其子节点给出。例如,下图展示了函数 的树表示。要将遗传编程应用于特定领域,用户必须定义要考虑的原始函数(例如,sin、cos、×、+、-、指数等),以及终结符(例如,x、y、常数如 2)。然后,遗传编程算法使用进化搜索来探索可以使用这些原始函数描述的庞大程序空间。与遗传算法类似,典型的遗传编程算法维护一个个体种群(在这种情况下是程序树)。在每次迭代中,它通过选择、交叉和变异产生新一代个体。种群中给定个体程序的适应度通常通过在一组训练数据上执行程序来确定。交叉操作通过用另一个父代程序的子树替换一个父代程序的随机选择的子树来执行。
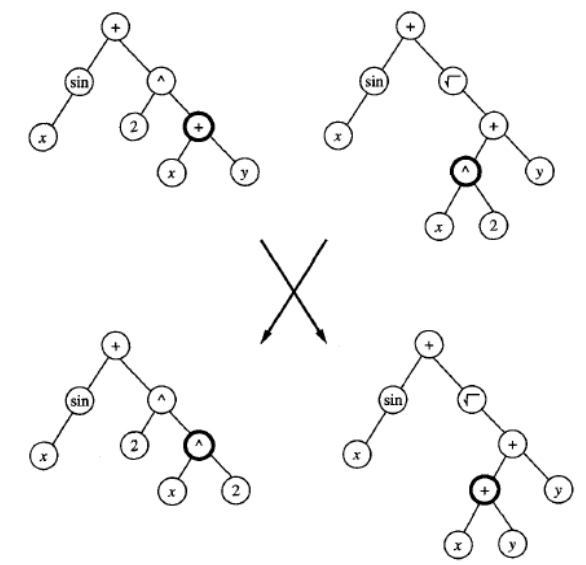
上图展示了一个典型的交叉操作。它描述了一组将 GP 应用于多个应用的实验。在他的实验中,10% 的当前种群(根据适应度概率性选择)在下一代中保持不变。新一代的其余部分通过对当前代中的程序对应用交叉来创建,同样是根据它们的适应度概率性选择。这组特定的实验中没有使用变异操作符。
示例说明
Koza (1992) 提出的一个说明性例子涉及学习一种堆叠图示方块的算法。任务是开发一种通用算法,将方块堆叠成一个拼写“universal”单词的单一堆栈,而与方块在世界中的初始配置无关。
可用于操作方块的动作只允许一次移动一个方块。特别是,堆栈顶部的方块可以移动到桌面,或者桌面上的方块可以移动到堆栈顶部。

在大多数 GP 应用中,问题表示的选择对解决问题的难易程度有显著影响。在 Koza 的公式中,用于为该任务组合程序的原始函数包括以下三个终结符参数:
- CS (current stack):指代堆栈顶部方块的名称,如果当前没有堆栈则为 F。
- TB (top correct block):指代堆栈上最顶部的方块的名称,使得它及其下方的方块都处于正确的顺序。
- NN (next necessary):指代堆栈中 TB 上方所需的下一个方块的名称,以拼写单词“universal”,如果不再需要方块则为 F。
可以看出,这种特定的终结符参数选择为描述用于此任务的方块操作程序提供了一种自然表示。相比之下,如果我们将终结符参数定义为每个方块的 x 和 y 坐标,那么任务的相对难度可想而知。
除了这些终结符参数,此应用程序中的程序语言还包括以下原始函数:
- (MS x) (move to stack):如果方块 x 在桌面上,此操作符将 x 移动到堆栈顶部并返回 T 值。否则,它不执行任何操作并返回 F 值。
- (MT x) (move to table):如果方块 x 在堆栈中的某个位置,这将堆栈顶部的方块移动到桌面并返回 T 值。否则,它返回 F 值。
- (EQ x y) (equal):如果 x 等于 y 则返回 T,否则返回 F。
- (NOT x):如果 x = F 则返回 T,如果 x = T 则返回 F。
- (DU x y) (do until):重复执行表达式 x 直到表达式 y 返回 T 值。
为了允许系统评估任何给定程序的适应度,Koza 提供了一组 166 个训练示例问题,代表了各种初始方块配置,包括不同难度的问题。任何给定程序的适应度被视为算法解决这些示例的数量。种群被初始化为 300 个随机程序。在 10 代之后,系统发现了以下程序,它解决了所有 166 个问题。
(EQ (DU (MT CS)(NOT CS)) (DU (MS NN)(NOT NN)) )
请注意,此程序包含两个 DU 或“Do Until”语句的序列。第一个语句重复地将堆栈的当前顶部移动到桌面,直到堆栈变空。第二个“Do Until”语句然后重复地将下一个必要的方块从桌面移动到堆栈。这里顶层 EQ 表达式的作用是提供一种语法上合法的方式来按顺序执行这两个“Do Until”循环。
令人有些惊讶的是,仅仅经过几代,这个 GP 就能够发现一个解决所有 166 个训练问题的程序。当然,系统完成此任务的能力强烈依赖于提供的原始参数和函数,以及用于评估适应度的训练示例集。
关于遗传编程的评论
如上例所示,遗传编程将遗传算法扩展到完整计算机程序的进化。尽管它必须搜索的假设空间巨大,但遗传编程已被证明在许多应用中产生了引人入胜的结果。O'Reilly 和 Oppacher (1994) 对 GP 与其他搜索计算机程序空间的方法(如爬山法和模拟退火)进行了比较。
虽然上述 GP 搜索示例相当简单,但 Koza 等人 (1996) 总结了 GP 在几个更复杂任务中的应用,例如设计电子滤波器电路和分类蛋白质分子片段。滤波器电路设计问题提供了一个复杂得多的例子。在这里,程序被进化以将一个简单的固定种子电路转换为最终电路设计。GP 用于构建其程序的原始函数是通过插入或删除电路组件和布线连接来编辑种子电路的函数。每个程序的适应度通过模拟其输出电路(使用 SPICE 电路模拟器)来计算,以确定该电路与所需滤波器的设计规范的匹配程度。更准确地说,适应度分数是所需和实际电路输出在 101 个不同输入频率下误差幅度的总和。在这种情况下,维持了大小为 640,000 的种群,选择产生 10% 的后代种群,交叉产生 89%,变异产生 1%。系统在 64 节点并行处理器上执行。在最初随机生成的种群中,产生的电路是如此不合理,以至于 SPICE 模拟器甚至无法模拟 98% 的电路行为。不可模拟电路的百分比在第一代后下降到 84.9%,在第二代后下降到 75.0%,并在后续世代平均下降到 9.6%。初始种群中最佳电路的适应度分数为 159,而 20 代后为 39,137 代后为 0.8。在 137 代后产生的最佳电路表现出与所需行为非常相似的性能。
在大多数情况下,遗传编程的性能关键取决于表示的选择和适应度函数的选择。因此,当前一个活跃的研究领域旨在自动发现和整合改进原始函数集子程序,从而允许系统动态改变它构建个体的原始函数。例如,参见 Koza (1994)。
Genetic programming (GP) is a form of evolutionary computation in which the individuals in the
evolving population are computer programs rather than bit strings. The basic genetic programming
approach and presents a broad range of simple programs that can be successfully learned by GP.
Representing Programs
Programs manipulated by a GP are typically represented by trees corresponding to the parse tree of the
program. Each function call is represented by a node in the tree, and the arguments to the function are
given by its descendant nodes. For example, below Figure illustrates this tree representation for the
function sin(x) +
x2
y . To apply genetic programming to a particular domain, the user must define
the primitive functions to be considered (e.g., sin, cos,
, +, -, exponential~), as well as the terminals
(e.g., x, y, constants such as 2). The genetic programming algorithm then uses an evolutionary search to
explore the vast space of programs that can be described using these primitives. As in a genetic
algorithm, the prototypical genetic programming algorithm maintains a population of individuals (in this
case, program trees). On each iteration, it produces a new generation of individuals using selection,
crossover, and mutation. The fitness of a given individual program in the population is typically
determined by executing the program on a set of training data. Crossover operations are performed by
replacing a randomly chosen subtree of one parent program by a subtree from the other parent
program.
Above Figure illustrates a typical crossover operation. It describes a set of experiments applying
a GP to a number of applications. In his experiments, 10% of the current population, selected
probabilistically according to fitness, is retained unchanged in the next generation. The remainder of
the new generation is created by applying crossover to pairs of programs from the current generation,
again selected probabilistically according to their fitness. The mutation operator was not used in this
particular set of experiments.
Illustrative Example
One illustrative example presented by Koza (1992) involves learning an algorithm for stacking the blocks
shown in below Figure The task is to develop a general algorithm for stacking the blocks into a single
stack that spells the word "universal," independent of the initial configuration of blocks in the world.
The actions available for manipulating blocks allow moving only a single block at a time. In particular,
the top block on the stack can be moved to the table surface, or a block on the table surface can be
moved to the top of the stack.
111
As in most GP applications, the choice of problem representation has a significant impact on the
ease of solving the problem. In Koza's formulation, the primitive functions used to compose programs
for this task include the following three terminal arguments:
CS (current stack), which refers to the name of the top block on the stack, or F if there is no
current stack.
TB (top correct block), which refers to the name of the topmost block on the stack, such that it
and those blocks beneath it are in the correct order.
NN (next necessary), which refers to the name of the next block needed above TB in the stack,
in order to spell the word "universal," or F if no more blocks are needed.
As can be seen, this particular choice of terminal arguments provides a natural representation for
describing programs for manipulating blocks for this task. Imagine, in contrast, the relative difficulty of
the task if we were to instead define the terminal arguments to be the x and y coordinates of each
block.
In addition to these terminal arguments, the program language in this application included the
following primitive functions:
(MS x) (move to stack), if block x is on the table, this operator moves x to the top of the stack
and returns the value T. Otherwise, it does nothing and returns the value F.
(MT x) (move to table), if block x is somewhere in the stack, this moves the block at the top of
the stack to the table and returns the value T. Otherwise, it returns the value F.
(EQ x y) (equal), which returns T if x equals y, and returns F otherwise.
(NOT x), which returns T if x = F, and returns F if x = T.
(DU x y) (do until), which executes the expression x repeatedly until expressiony returns the
value T.
To allow the system to evaluate the fitness of any given program, Koza provided a set of 166 training
example problems representing a broad variety of initial block configurations, including problems of
differing degrees of difficulty. The fitness of any given program was taken to be the number of these
examples solved by the algorithm. The population was initialized to a set of 300 random programs.
After 10 generations, the system discovered the following program, which solves all 166 problems.
(EQ (DU (MT CS)(NOT CS)) (DU (MS NN)(NOT NN)) )
Notice this program contains a sequence of two DU, or "Do Until" statements. The first repeatedly
112
moves the current top of the stack onto the table, until the stack becomes empty. The second "Do
Until" statement then repeatedly moves the next necessary block from the table onto the stack. The
role played by the top level EQ expression here is to provide a syntactically legal way to sequence these
two "Do Until" loops.
Somewhat surprisingly, after only a few generations, this GP was able to discover a program that solves
all 166 training problems. Of course the ability of the system to accomplish this depends strongly on the
primitive arguments and functions provided, and on the set of training example cases used to evaluate
fitness.
Remarks on Genetic Programming
As illustrated in the above example, genetic programming extends genetic algorithms to the
evolution of complete computer programs. Despite the huge size of the hypothesis space it must
search, genetic programming has been demonstrated to produce intriguing results in a number of
applications. A comparison of GP to other methods for searching through the space of computer
programs, such as hillclimbing and simulated annealing, is given by O'Reilly and Oppacher (1994).
While the above example of GP search is fairly simple, Koza et al. (1996) summarize the use of a GP in
several more complex tasks such as designing electronic filter circuits and classifying segments of
protein molecules. The filter circuit design problem provides an example of a considerably more
complex problem. Here, programs are evolved that transform a simple fixed seed circuit into a final
circuit design. The primitive functions used by the GP to construct its programs are functions that edit
the seed circuit by inserting or deleting circuit components and wiring connections. The fitness of each
program is calculated by simulating the circuit it outputs (using the SPICE circuit simulator) to determine
how closely this circuit meets the design specifications for the desired filter. More precisely, the fitness
score is the sum of the magnitudes of errors between the desired and actual circuit output at 101
different input frequencies. In this case, a population of size 640,000 was maintained, with selection
producing 10% of the successor population, crossover producing 89%, and mutation producing 1%. The
system was executed on a 64-node parallel processor. Within the first randomly generated population,
the circuits produced were so unreasonable that the SPICE simulator could not even simulate the
behavior of 98% of the circuits. The percentage of unsimulatable circuits dropped to 84.9% following
the first generation, to 75.0% following the second generation, and to an average of 9.6% over
succeeding generations. The fitness score of the best circuit in the initial population was 159, compared
to a score of 39 after 20 generations and a score of 0.8 after 137 generations. The best circuit, produced
after 137 generations, exhibited performance very similar to the desired behavior.
In most cases, the performance of genetic programming depends crucially on the choice of
representation and on the choice of fitness function. For this reason, an active area of current research
is aimed at the automatic discovery and incorporation of subroutines that improve on the original set of
primitive functions, thereby allowing the system to dynamically alter the primitives from which it
constructs individuals. See, for example, Koza (1994).