Python机器学习项目
神经网络的架构指的是网络的层数、每层中的单元数量以及单元之间如何连接等元素。由于神经网络松散地受到人脑工作方式的启发,这里**“单元 (unit)”**一词代表了我们生物学上所说的神经元。
就像神经元在大脑中传递信号一样,单元从先前的单元接收一些值作为输入,执行计算,然后将新值作为输出传递给其他单元。这些单元分层形成网络,最少从一个输入值层和一个输出值层开始。**“隐藏层 (hidden layer)”**一词用于指代输入层和输出层之间的所有层,即那些“隐藏”于现实世界之外的层。
不同的架构可以产生截然不同的结果,因为性能可以被认为是架构、参数、数据和训练持续时间等因素的函数。
将以下代码行添加到你的文件中,以全局变量的形式存储每层的单元数量。这允许我们在一个地方更改网络架构,并且在本教程结束时,你可以亲自测试不同数量的层和单元将如何影响我们模型的结果:
main.py
...
n_input = 784 # 输入层 (28x28 像素)
n_hidden1 = 512 # 第 1 个隐藏层
n_hidden2 = 256 # 第 2 个隐藏层
n_hidden3 = 128 # 第 3 个隐藏层
n_output = 10 # 输出层 (0-9 数字)
下图展示了我们设计的架构的视觉表示,每层都与周围层完全连接:
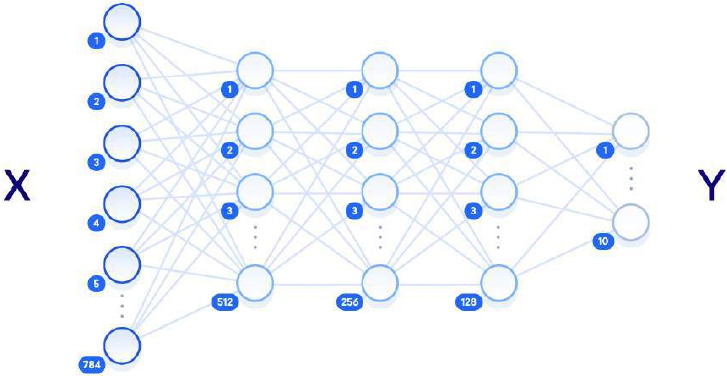
神经网络图
“深度神经网络 (deep neural network)”这个术语与隐藏层的数量有关,“浅层 (shallow)”通常意味着只有一个隐藏层,“深度 (deep)”则指多个隐藏层。在有足够训练数据的情况下,一个拥有足够数量单元的浅层神经网络理论上应该能够表示任何深度神经网络可以表示的函数。但通常使用一个较小的深度神经网络来完成相同的任务会更具计算效率,而浅层网络则需要指数级更多的隐藏单元。浅层神经网络也经常遇到过拟合 (overfitting),即网络基本上记住了它所见过的训练数据,并且无法将知识泛化到新数据。这就是深度神经网络更常用的原因:原始输入数据和输出标签之间的多层允许网络学习不同抽象级别的特征,使网络本身能够更好地泛化。
这里还需要定义的神经网络的其他元素是超参数 (hyperparameters)。与在训练期间更新的参数不同,这些值是最初设置的,并在整个过程中保持不变。在你的文件中,设置以下变量和值:
main.py
...
learning_rate = 1e-4
n_iterations = 1000
batch_size = 128
dropout = 0.5
学习率 (learning rate) 表示在学习过程的每个步骤中参数将调整多少。这些调整是训练的关键组成部分:每次通过网络后,我们会稍微调整权重,试图减少损失。较大的学习率可以更快收敛,但也可能在更新时超出最优值。迭代次数 (n_iterations) 指的是我们执行训练步骤的次数,批量大小 (batch_size) 指的是我们在每个步骤中使用的训练示例数量。Dropout (dropout) 变量表示我们随机消除一些单元的阈值。我们将在最终隐藏层中使用 dropout,使每个单元在每个训练步骤中都有 50% 的机会被消除。这有助于防止过拟合。
我们现在已经定义了神经网络的架构以及影响学习过程的超参数。下一步是将网络构建为 TensorFlow 图。
准备好进入下一步,将网络构建为 TensorFlow 图了吗?
Step 3 — Defining the Neural Network Architecture
The architecture of the neural network refers to elements such as the
number of layers in the network, the number of units in each layer, and
how the units are connected between layers. As neural networks are
loosely inspired by the workings of the human brain, here the term unit
is used to represent what we would biologically think of as a neuron.
Like neurons passing signals around the brain, units take some values
from previous units as input, perform a computation, and then pass on
the new value as output to other units. These units are layered to form
the network, starting at a minimum with one layer for inputting values,
and one layer to output values. The term hidden layer is used for all of
the layers in between the input and output layers, i.e. those “hidden”
from the real world.
Different architectures can yield dramatically different results, as the
performance can be thought of as a function of the architecture among
other things, such as the parameters, the data, and the duration of
training.
Add the following lines of code to your file to store the number of
units per layer in global variables. This allows us to alter the network
architecture in one place, and at the end of the tutorial you can test for
yourself how different numbers of layers and units will impact the
results of our model:
main.py
...
n_input = 784
# input layer (28x28 pixels)
n_hidden1 = 512
# 1st hidden layer
n_hidden2 = 256
# 2nd hidden layer
n_hidden3 = 128
# 3rd hidden layer
n_output = 10
# output layer (0-9 digits)
The following diagram shows a visualization of the architecture we’ve
designed, with each layer fully connected to the surrounding layers:
Diagram of a neural network
The term “deep neural network” relates to the number of hidden
layers, with “shallow” usually meaning just one hidden layer, and
“deep” referring to multiple hidden layers. Given enough training data, a
shallow neural network with a sufficient number of units should
theoretically be able to represent any function that a deep neural network
can. But it is often more computationally efficient to use a smaller deep
neural network to achieve the same task that would require a shallow
network with exponentially more hidden units. Shallow neural networks
also
often
encounter
overfitting,
where
the network essentially
memorizes the training data that it has seen, and is not able to generalize
the knowledge to new data. This is why deep neural networks are more
commonly used: the multiple layers between the raw input data and the
output label allow the network to learn features at various levels of
abstraction, making the network itself better able to generalize.
Other elements of the neural network that need to be defined here are
the hyperparameters. Unlike the parameters that will get updated during
training, these values are set initially and remain constant throughout the
process. In your file, set the following variables and values:
main.py
...
learning_rate = 1e-4
n_iterations = 1000
batch_size = 128
dropout = 0.5
The learning rate represents how much the parameters will adjust at
each step of the learning process. These adjustments are a key component
of training: after each pass through the network we tune the weights
slightly to try and reduce the loss. Larger learning rates can converge
faster, but also have the potential to overshoot the optimal values as they
are updated. The number of iterations refers to how many times we go
through the training step, and the batch size refers to how many training
examples we are using at each step. The dropout variable represents a
threshold at which we eliminate some units at random. We will be using
dropout in our final hidden layer to give each unit a 50% chance of
being eliminated at every training step. This helps prevent overfitting.
We have now defined the architecture of our neural network, and the
hyperparameters that impact the learning process. The next step is to
build the network as a TensorFlow graph.