引言

当我们谈论“神经网络”时，我们指的是人工神经网络（ANN）。ANN 的思想基于生物神经网络，例如生物的大脑。

神经网络的基本结构——无论是人工的还是生物的——都是神经元。生物学中的神经元由三个主要部分组成：胞体（细胞体）、树突和轴突。

树突以树状方式从胞体分支出来，并且随着每次分支而变细。它们在突触处接收来自其他神经元的信号（脉冲）。轴突——总是只有一个——也从胞体发出，通常比树突延伸得更长。轴突用于将神经元的输出发送到其他神经元，或者更确切地说，发送到其他神经元的突触。

生物神经元

以下图片由 Quasar Jarosz 提供，经维基百科授权，对此进行了说明：

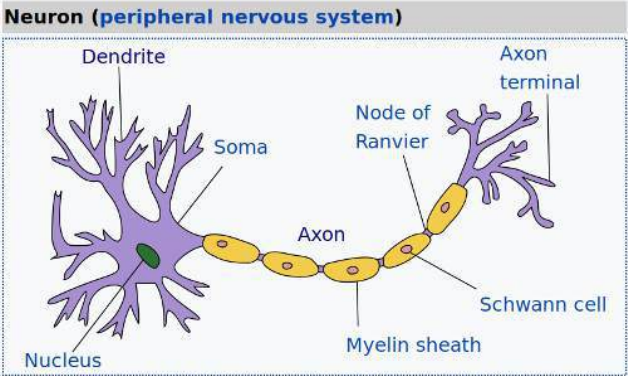
（图片：一个生物神经元的示意图，显示了胞体、树突和轴突）

生物神经元和人工神经元的抽象

尽管上面的图片对于生物学家来说已经是一种抽象，我们仍然可以进一步抽象它：

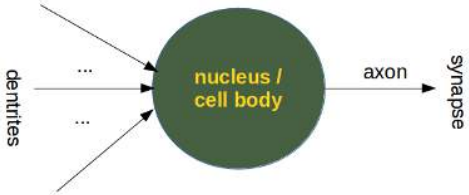
人工神经网络的感知器模拟了生物神经元。

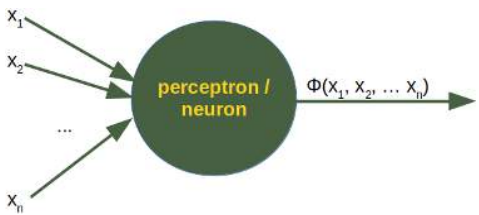
感知器或神经元内部发生的事情非常简单。输入信号乘以权重值，即每个输入都有其对应的权重。通过这种方式，可以为每个 xi​ 单独调整输入。我们可以将所有输入视为输入向量，将相应的权重视为权重向量。

当信号进入时，它会乘以分配给该特定输入的权重值。也就是说，如果一个神经元有三个输入，那么它就有三个可以单独调整的权重。这些权重通常在学习阶段进行调整。

此后，修改后的输入信号被求和。也可以额外向这个和中添加一个所谓的偏置（bias） “b”。偏置是一个值，也可以在学习阶段进行调整。

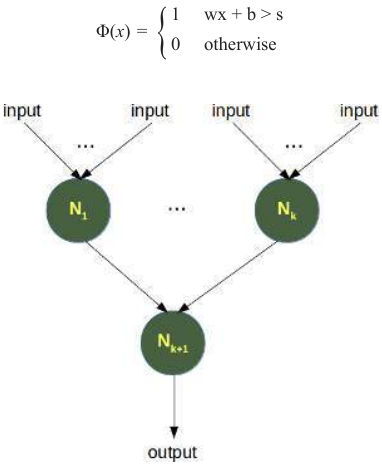
最后，必须确定实际输出。为此，将激活函数或阶跃函数 Φ 应用于输入值的加权和。

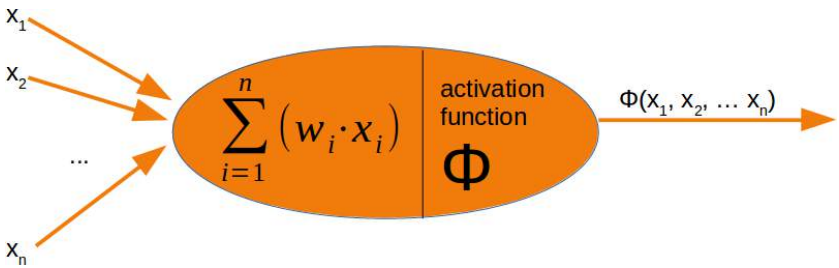
激活函数最简单的形式是二元函数。如果求和结果大于某个阈值 s，则 Φ 的结果将为 1，否则为 0。

动物神经元数量

我们将在接下来的章节中研究各种大小和结构的人工神经网络。了解一些动物的神经元总数是很有趣的：

  • 蛔虫：302

  • 水母：

（内容截断）

INTRODUCTION
When we say "Neural Networks", we
mean artificial Neural Networks (ANN).
The idea of ANN is based on biological
neural networks like the brain of living
being.
The basic structure of a neural network -
both an artificial and a living one - is the
neuron. A neuron in biology consists of
three major parts: the soma (cell body),
the dendrites and the axon.
The dendrites branch of from the soma in
a tree-like way and become thinner with
every branch. They receive signals
(impulses) from other neurons at synapses. The axon - there is always only one - also leaves the soma and
usually tend to extend for longer distances than the dentrites. The axon is used for sending the output of the
neuron to other neurons or better to the synapsis of other neurons.
BIOLOGICAL NEURON
The following image by Quasar Jarosz, courtesy of Wikipedia, illustrates this:
92
ABSTRACTION OF A BIOLOGICAL NEURON AND ARTIFICIAL NEURON
Even though the above image is already an abstraction for a biologist, we can further abstract it:
A perceptron of artificial neural networks is simulating a biological neuron.
It is amazingly simple, what is going on inside the body of a perceptron or neuron. The input signals get
multiplied by weight values, i.e. each input has its corresponding weight. This way the input can be adjusted
individually for every x i. We can see all the inputs as an input vector and the corresponding weights as the
weights vector.
When a signal comes in, it gets multiplied by a weight value that is assigned to this particular input. That is, if
a neuron has three inputs, then it has three weights that can be adjusted individually. The weights usually get
adjusted during the learn phase.
After this the modified input signals are summed up. It is also possible to add additionally a so-called bias 'b'
to this sum. The bias is a value which can also be adjusted during the learn phase.
Finally, the actual output has to be determined. For this purpose an activation or step function Φ is applied to
the weighted sum of the input values.
93
The simplest form of an activation function is a binary function. If the result of the summation is greater than
some threshold s, the result of Φ will be 1, otherwise 0.
Φ(x) =
 {
 1
 0
 wx otherwise
 + b > s
NUMBER OF NEURON IN ANIMALS
We will examine in the following chapters artificial neuronal networks of various sizes and structures. It is
interesting to have a look at the total numbers of neurons some animals have:
• Roundworm: 302
• Jellyfish
94
In [ ]:

最后修改: 2025年06月30日 星期一 10:02