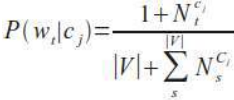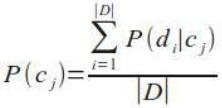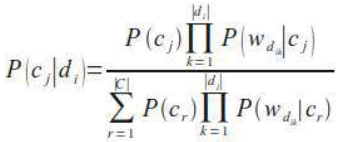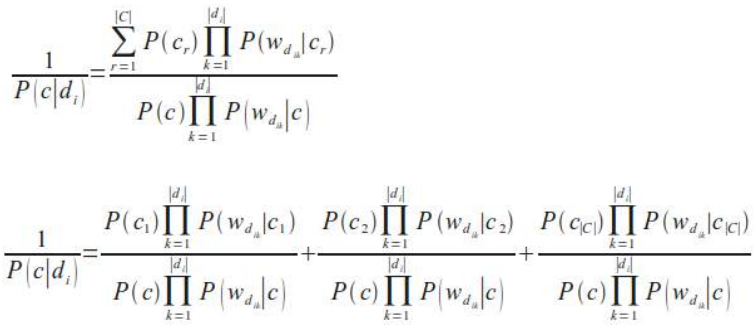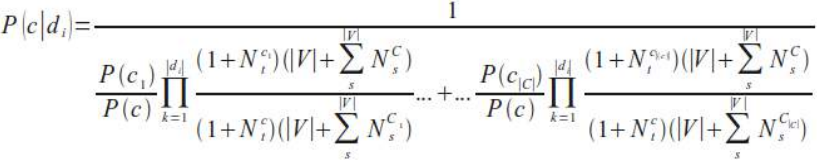机器学习Python教程
引言
文档分类/归类是信息科学中的一个主题,信息科学涉及信息的收集、分析、分类、归类、处理、检索、存储和传播。
这听起来可能非常抽象,但如今有很多情况,公司需要对文档进行自动分类或归类。试想一家大型公司,每天有成千上万份纸质或电子形式的邮件涌入。其中许多邮件没有具体的收件人姓名或部门。
必须有人阅读这些文本,并决定这封信属于哪种类型(“更改地址”、“投诉信”、“产品咨询”等等),以及该文档应该发送给谁。这个“某人”可以是一个自动化文本分类系统。
自动化文本分类,也称为文本归类,其历史可以追溯到 20 世纪 60 年代初。但过去二十年里,由于互联网的扩展,可用在线文档的惊人增长,重新激化了人们对自动化文档分类和数据挖掘的兴趣。最初,文本分类侧重于启发式方法,即通过应用基于专家知识的一系列规则来解决任务。这种方法被证明效率低下,因此现在焦点已转向全自动学习和聚类方法。
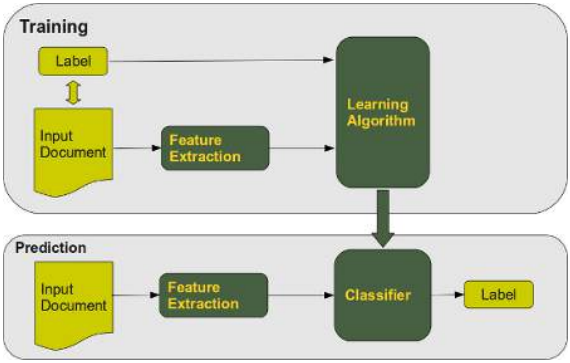 文本分类的任务在于根据文档的语义内容,将文档分配给一个或多个类别。文档(或文本)分类以两种模式运行:
文本分类的任务在于根据文档的语义内容,将文档分配给一个或多个类别。文档(或文本)分类以两种模式运行:
-
训练阶段
-
预测(或分类)阶段
训练阶段可以分为三种:
-
有监督文档分类:由外部机制(通常是人工反馈)执行,提供文档正确分类所需的信息。
-
半监督文档分类:有监督和无监督分类的混合:一些文档或文档的部分由外部辅助进行标记。
-
无监督文档分类:完全在没有参考外部信息的情况下执行。
我们将使用朴素贝叶斯在 Python 中实现一个文本分类器。朴素贝叶斯是最常用的文本分类器,也是文本分类研究的重点。朴素贝叶斯分类器基于应用贝叶斯定理,并带有强独立性假设。“强独立性”意味着:某个类别的特定特征的存在或缺失与任何其他特征的存在或缺失不相关。朴素贝叶斯非常适合多类别文本分类。
形式定义
令 \(C={c_1,c_2 \text{,…} c_m}\) 为一组类别
令 \(D={d_1,d_2,\text{…} d_n}\) 为一组文档。
文本分类的任务在于为 的每对 (\(c_i\),\(d_j\))(其中 且 )分配一个 0 或 1 的值,即如果文档 \(d_j\) 不属于 \(c_i\),则值为 0。
这种映射有时被称为决策矩阵:

解决此任务的主要方法有:
-
朴素贝叶斯
-
支持向量机
-
最近邻
朴素贝叶斯分类器
贝叶斯分类器是一种简单的概率分类器,基于应用带有强(朴素)独立性假设的贝叶斯定理,即“独立特征模型”。换句话说:朴素贝叶斯分类器假设某个类别的特定特征的存在(或缺失)与任何其他特征的存在(或缺失)不相关。
朴素贝叶斯分类器的形式推导:

令 \(C={c_1,c_2 \text{,…} c_m}\) 为一组类别
令 \(D={d_1,d_2,\text{…} d_n}\) 为一组文档。
每个文档都用一个类别标记。
文档集 D 用于训练分类器。
分类在于为一个未知文档选择最可能的类别。
单词\(w_t\)在文档 \(d_i\) 中出现的次数将表示为 \(N_{it}\)。\(N_t^C\) 表示单词 \(w_t\) 在给定类别 C 的所有文档中出现的次数。
如果 \(d_i\) 被标记为 \(c_j\),则 \(P(d_i∣c_j)\) 为 1,否则为 0。
给定类别 \(c_j\) 的单词 \(w_t\) 的概率为:
类别 \(c_j\) 的概率是 \(c_j\) 的文档数量与所有类别文档数量(即学习集)的商:
最后,我们得到了对未知文档进行分类所需的公式,即给定文档 \(d_i\) 的类别 \(c_j\) 的概率:
不幸的是,我们刚刚给出的 P(c∣\(d_i\)) 公式在数值上不稳定,因为分母可能由于舍入误差而为零。我们通过计算倒数并将其重新表述为稳定商的和来改变这一点:
我们可以将前面的公式改写成以下形式,即我们最终的朴素贝叶斯分类公式,也是我们将在下一章的 Python 实现中使用的公式:
延伸阅读
关于文本分类的文章有很多。我们只列举了一些我们工作中使用的文章:
-
Fabrizio Sebastiani. "A tutorial on automated text categorisation." In Analia Amandi and Alejandro Zunino (eds.), Proceedings of the 1st Argentinian Symposium on Artificial Intelligence (ASAI'99), Buenos Aires, AR, 1999, pp. 7-35.
-
Lewis, David D. "Naive (Bayes) at Forty: The independence assumption in informal retrieval." Lecture Notes in Computer Science (1998), 1398, Issue: 1398, Publisher: Springer, Pages: 4-15.
-
K. Nigam, A. McCallum, S. Thrun and T. Mitchell. "Text classification from labeled and unlabeled documents using EM." Machine Learning 39 (2000) (2/3), pp. 103-134.
INTRODUCTION
Document classification/categorization is a topic in information science, a
science dealing with the collection, analysis, classification, categorization,
manipulation, retrieval, storage and propagation of information.
This might sound very abstract, but there are lots of situations nowadays,
where companies are in need of automatic classification or categorization
of documents. Just think about a large company with thousands of
incoming mail pieces per day, both electronic or paper based. Lot's of these
mail pieces are without specific addressee names or departments.
Somebody has to read these texts and has to decide what kind of a letter it is ("change of address", "complaints
letter", "inquiry about products", and so on) and to whom the document should be proceeded. This
"somebody" can be an automated text classification system.
Automated text classification,
also called categorization of texts,
has a history, which dates back to
the beginning of the 1960s. But
the incredible increase in
available online documents in the
last two decades, due to the
expanding internet, has
intensified and renewed the
interest in automated document
classification and data mining. In
the beginning text classification
focussed on heuristic methods,
i.e. solving the task by applying a
set of rules based on expert
knowledge. This approach proved
to be highly inefficient, so
nowadays the focus has turned to
fully automatic learning and clustering methods.
The task of text classification consists in assigning a document to one or more categories, based on the
semantic content of the document. Document (or text) classification runs in two modes:
••The training phase and the
prediction (or classification) phase.
322
The training phase can be divided into three kinds:
•••supervised document classification is performed by an external mechanism, usually human
feedback, which provides the necessary information for the correct classification of documents,
semi-supervised document classification, a mixture between supervised and unsupervised
classification: some documents or parts of documents are labelled by external assistance,
unsupervised document classification is entirely executed without reference to external
information.
We will implement a text classifier in Python using Naive Bayes. Naive Bayes is the most commonly used text
classifier and it is the focus of research in text classification. A Naive Bayes classifier is based on the
application of Bayes' theorem with strong independence assumptions. "Strong independence" means: the
presence or absence of a particular feature of a class is unrelated to the presence or absence of any other
feature. Naive Bayes is well suited for multiclass text classification.
FORMAL DEFINITION
Let C = { c1, c2, ... cm} be a set of categories (classes) and D = { d1, d2, ... dn} a set of documents.
The task of the text classification consists in assigning to each pair ( ci, dj ) of C x D (with 1 ≤ i ≤ m and 1 ≤ j
≤ n) a value of 0 or 1, i.e. the value 0, if the document dj doesn't belong to ci
This mapping is sometimes referred to as the decision matrix:
d 1
...
d j
...
d n
c 1
a 11
...
a 1j
...
a1n
...
...
...
...
...
...
c i
a i1
...
aij
...
ain
...
...
...
...
...
...
cm
am1
...
a mj
...
a mn
The main approaches to solve this task are:
• Naive Bayes
• Support Vector Machine
▪ Nearest Neighbour
323
NAIVE BAYES CLASSIFIER
A Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong (naïve)
independence assumptions, i.e. an "independent feature model". In other words: A naive Bayes classifier
assumes that the presence (or absence) of a particular feature of a class is unrelated to the presence (or
absence) of any other feature.
FORMAL DERIVATION OF THE NAIVE BAYES CLASSIFIER:
Let C = { c1, c2, ... cm} be a set of classes or categories
and D = { d1, d2, ... dn} be a set of documents.
Each document is labeled with a class.
The set D of documents is used to train the classifier.
Classification consists in selecting the most probable class
for an unknown document.
The number of times a word wt occurs within a document
di will be denoted as Nit. NtC denotes the number of times
a word wt ocurs in all documents of a given class C.
P(di|cj) is 1, if di is labelled as cj, 0 otherwise
The probability for a word w t given a class c j :
The probability for a class cj is the quotient of the number of Documents of cj and the number of documents of
all classes, i.e. the learn set:
Finally, we come to the formula we need to classify an unknown document, i.e. the probability for a class cj
given a document di:
324
Unfortunately, the formula of P(c|di) we have just given is numerically not stable, because the denominator
can be zero due to rounding errors. We change this by calculating the reciprocal and reformulate the
expression as a sum of stable quotients:
We can rewrite the previous formula into the following form, our final Naive Bayes classification formula, the
one we will use in our Python implementation in the following chapter:
FURTHER READING
There are lots of articles on text classification. We just name a few, which we have used for our work:
• Fabrizio Sebastiani. A tutorial on automated text categorisation. In Analia Amandi and
325
••Alejandro Zunino (eds.), Proceedings of the 1st Argentinian Symposium on Artificial
Intelligence (ASAI'99), Buenos Aires, AR, 1999, pp. 7-35.
Lewis, David D., Naive (Bayes) at Forty: The independence assumption in informal retrieval,
Lecture Notes in Computer Science (1998), 1398, Issue: 1398, Publisher: Springer, Pages: 4-15
K. Nigam, A. McCallum, S. Thrun and T. Mitchell, Text classification from labeled and
unlabeled documents using EM, Machine Learning 39 (2000) (2/3), pp. 103-134.