节: 多边函数的特征 | 4.5 多元函数的特点-interactive

章节大纲

Lesson Objectives
::经验教训目标

Identify the end behavior of a function based on the degree and coefficient .
::根据程度和系数确定函数的最终行为。

Understand how the multiplicity of a factor affects the behavior of the graph of a polynomial at its $\begin{aligned} x - \end{aligned}$ intercept .
::了解一个因素的多重性如何影响多面形图 X 界面的图形行为。

Determine the intervals where a polynomial is positive and negative.
::确定多面体为正和负的间隔。

Graph a polynomial function .
::图形多面函数。

Compare the properties of two quadratics in the different forms.
::比较两种不同形式的二次方位的特性。

Introduction: Characteristics of Polynomial Functions
::导言:多功能的特点

Use the interactive below to explore how the $\begin{aligned} a \end{aligned}$ coefficient and the degree determine the shape of a polynomial.
::利用下面的交互作用来探讨系数和程度如何决定多元数值的形状。

INTERACTIVE

Graphing Polynomials

Use the sliders to change the leading coefficient $(a)$ and degree $\left(n\right)$ .
::使用滑动符改变主要系数(a)和程度。

Notice how using the sliders to change the values of $a$ and $n$ impacts the shape and position of the graph.
::注意使用滑动符改变 n 和 n 的值如何影响图形的形状和位置。

Drag the screen to pan and zoom the graph.
::拖曳屏幕以调色板并缩放图形。

Progress

0 / 2

Complete the table to describe the end behavior rules of polynomials ("up" or "down"):
::完成用于描述多面形(“上”或“下”)最终行为规则的表格 :

@$\begin{align*}a\end{align*}@$ is positive

@$\begin{align*}a\end{align*}@$ is negative

degree is even

left side: Enter your answer
::左左侧:输入答案

right side: Enter your answer
::右侧右侧:输入您的答复

left side: Enter your answer
::左左侧:输入答案

right side: Enter your answer
::右侧右侧:输入您的答复

degree is odd

left side: Enter your answer
::左左侧:输入答案

right side: Enter your answer
::右侧右侧:输入您的答复

left side: Enter your answer
::左左侧:输入答案

right side: Enter your answer
::右侧右侧:输入您的答复

Activity 1: End Behavior of Polynomial Graphs
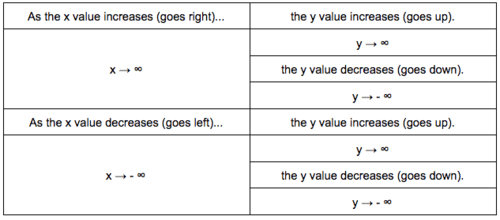
::活动1:多面图的结束行为

In the introduction , the terms “up” and “down” were used to describe the end behavior of a polynomial function. However, terms like “increases” and “decreases” are more mathematically precise . Additionally, to describe whether a function is increasing or decreasing, you should describe the direction along the $\begin{aligned} x - \end{aligned}$ axis in which you are moving. To say that the right side of a polynomial points up means that as the $\begin{aligned} x - \end{aligned}$ value increases ( as you go to the right ), the $\begin{aligned} y - \end{aligned}$ value increases (points up).
::在导言中,“上”和“下”两词用来描述多边函数的结束行为。然而,“增加”和“减少”等词在数学上更为精确。此外,为了描述一个函数在增加还是减少,您应该描述您移动的 x 轴方向。如果说一个多元点的右侧意味着随着X 值的增加(您向右),Y 值的增加(您向右),y 值的增加( 向上点) 。

This can also be stated using mathematical notation. When the $\begin{aligned} x - \end{aligned}$ value increases , it is written as $\begin{aligned} x \to \infty \end{aligned}$ because it is increasing toward infinity. When the $\begin{aligned} x - \end{aligned}$ value decreases , it is written as $\begin{aligned} x \to - \infty \end{aligned}$ because it is decreasing toward negative infinity.
::也可以用数学符号来表示。当 x 值增加时, 它被写成 x , 因为它正在向无穷度增长。当 x 值减少时, 它被写成 x , 因为它正在向负无穷度下降。

lesson content

T his notation can be used to write the rules for the end behavior of a polynomial function, as derived in the introduction.
::此标记可用于写入导言中导出的多边函数结束行为的规则。

lesson content

Answer the questions below to practice using these rules.
::回答以下使用这些规则的实践问题。

Discussion Question : Is it possible for a function with an odd degree to have no real roots? Is it possible for a polynomial with an even degree to have no real roots?
::讨论问题:具有奇特程度的函数是否可能没有真正的根?具有同等程度的多元婚姻是否可能没有真正的根?

Activity 2: Multiplicities
::活动2:多种用途

T he previous section, Roots of a Polynomial Equation , introduced zeros of a higher degree polynomial function, representing the x- intercepts , that repeated. T he number of times a zero repeats is referred to using the term multiplicity . Use the interactive below to explore how multiplicity affects a graph.
::上一节“多元等式的根”中引入了代表重复的 X 拦截的更高度多元函数的零。重复的零次数是指使用多重性这一术语的次数。使用下面的交互性来探索多重性如何影响一个图形。

INTERACTIVE

Multiplicities of Polynomials

See the graph of function, $f(x) = a(x - 1)(x - 4)^n(x - 7)$

::见函数图, f(x) =a(x-1)(x-4)n(x-7)

Drag the sliders to change the values of $a$ and $n$
::拖动滑动滑动器以更改 n 和 a 的值

When a zero has a multiplicity of 1, the function normally passes through the x-intercept.
::当零有多个 1 时,函数通常通过 X 界面。

When a zero has a multiplicity of 2, the function bounces off the x-intercept forming a parabola-like shape.
::当一个零的多重值为2时,函数会从形成类似抛物线形状的 X 界面中反弹。

When a zero has a multiplicity of 3, the function passes through x-intercept, forming a shape that the function $\begin{aligned} f (x) = x^{3} \end{aligned}$ has.
::当零的多重值为 3 时,函数通过 x 界面,形成函数 f( x) =x3 的形状。

Make and test a conjecture about how multiplicity relates to the shape formed when the graph passes through the x-intercept.
::设定并测试一个猜想,即当图形通过 X 界面时,多重性与形状的形成有何关联。

Coupl ed with your knowledge of end behavior, it makes it possible to predict whether the graph of a function will be positive or negative over specific intervals. Use the interactive below to explore another trick to figure this out.
::结合你对最终行为的了解, 它可以预测函数的图形是正的还是负的, 在特定的时间间隔内。使用下面的交互功能来探索另一个技巧来解决这个问题。

INTERACTIVE

Positive or Negative over an Interval

Type a number in the given interval.
::在给定间隔中键入数字。

Determine whether each factor will be positive or negative when substituting that number for $x.$
::确定在将数字替换为 x 时,每个因素是正的还是负的。

From that, you can determine if that entire interval is positive or negative.
::从中,您可以确定整个间隔是正或负。

Press "Next Interval" to repeat the process for each interval.
::按下“ 下一个间隔” 来重复每个间隔的过程。

Answer the questions below to practice identifying the positivity of a function over intervals defined by the x-intercepts.
::回答下述问题,以便从实践上确定一项职能在X调查确定的时间间隔内是否具有积极性。

Activity 3: Using Characteristics to Graph Polynomial Functions
::活动3:在图形多面函数中使用特征

Use the interactive below to practice graphing polynomial functions using their characteristics.
::使用下方的交互功能,使用其特性进行多面函数的图形绘制。

INTERACTIVE

Finding Polynomials

Enter the $x$ values for the roots of the equation in the input box.
::在输入框中输入方程式根的 x 值。

They will appear on the grid.
::他们会出现在网格上

Once you have all of the roots, choose the box that the graph would be in based on the interval.
::一旦您拥有了全部根, 请根据间隔选择图形所在的框。

If you get it right, the graph will appear where the box was and you can move to the next interval.
::如果正确的话, 图形将出现在框所在的位置, 您可以移动到下一个间隔。

Wrap-Up: Review Questions
::总结:审查问题

Summary
::摘要

For even functions:
::对于偶数函数 :

If the leading coefficient is positive: as $\begin{aligned} x \to + \infty, y \to + \infty \end{aligned}$
::如果主要系数是正数: as x, y

If the leading coefficient is positive: as $\begin{aligned} x \to - \infty, y \to + \infty \end{aligned}$
::如果主要系数是正数: as x, y

If the leading coefficient is negative: as $\begin{aligned} x \to + \infty, y \to - \infty \end{aligned}$
::如果主要系数为负: x,y。

If the leading coefficient is negative: as $\begin{aligned} x \to - \infty, y \to - \infty \end{aligned}$
::如果主要系数为负: x,y。

For odd functions:
::对于奇数函数 :

If the leading coefficient is positive: as $\begin{aligned} x \to + \infty, y \to + \infty \end{aligned}$
::如果主要系数是正数: as x, y

If the leading coefficient is positive: as $\begin{aligned} x \to - \infty, y \to - \infty \end{aligned}$
::如果主要系数是正数: as x, y

If the leading coefficient is negative: as $\begin{aligned} x \to + \infty, y \to - \infty \end{aligned}$
::如果主要系数为负: x,y。

If the leading coefficient is negative: as $\begin{aligned} x \to - \infty, y \to + \infty \end{aligned}$
::如果主要系数为负: x,y。

The multiplicity is the number of times a factor appears in the factors of a polynomial.
::多重性是多元性因素中一个因素出现的次数。

When a zero has a multiplicity of 1, the function passes through the x-intercept.
::当零有多个 1 时,函数通过 X 界面。

When a zero has a multiplicity of 2, the function bounces off the x-axis at the value of the zero.
::当一个零的乘积为2时,函数从X轴反弹,其值为零。

When a zero has a multiplicity of 3, the function passes through the x-intercept, forming a shape that the function $\begin{aligned} f (x) = x^{3} \end{aligned}$ has.
::当零的多重值为 3 时,函数通过 x 界面,形成函数 f( x) =x3 的形状。

章节大纲

Introduction: Characteristics of Polynomial Functions ::导言:多功能的特点

Activity 1: End Behavior of Polynomial Graphs ::活动1:多面图的结束行为

Activity 2: Multiplicities ::活动2:多种用途

Activity 3: Using Characteristics to Graph Polynomial Functions ::活动3:在图形多面函数中使用特征

Wrap-Up: Review Questions ::总结:审查问题

Summary ::摘要

Introduction: Characteristics of Polynomial Functions
::导言:多功能的特点

Activity 1: End Behavior of Polynomial Graphs
::活动1:多面图的结束行为

Activity 2: Multiplicities
::活动2:多种用途

Activity 3: Using Characteristics to Graph Polynomial Functions
::活动3:在图形多面函数中使用特征

Wrap-Up: Review Questions
::总结:审查问题

Summary
::摘要