4.5 多元函数的特点-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 多边函数的特征

  Collapse Expand

  多边函数的特征

  播放段落

  Lesson Objectives
  ::经验教训目标

  播放段落
  • Identify the end behavior of a function based on the degree and coefficient .
    ::根据程度和系数确定函数的最终行为。
  播放段落
  • Understand how the multiplicity of a factor affects the behavior of the graph of a polynomial at its $\begin{array}{r}x\text{-}\end{array}$ intercept .
    ::了解一个因素的多重性 如何影响多面形图 X 界面的图形行为 。
  播放段落
  • Determine the intervals where a polynomial is positive and negative.
    ::确定多面体为正和负的间隔。
  播放段落
  • Graph a polynomial function .
    ::图形多面函数。
  播放段落
  • Compare the properties of two quadratics in the different forms.  
    ::比较两种不同形式的二次方位的特性。

  ---

  播放段落

  Introduction: Characteristics of Polynomial Functions
  ::导言:多功能的特点

  播放段落

  Use the interactive below to explore how the $\begin{array}{r}a\end{array}$  coefficient and the degree determine the shape of a polynomial.
  ::利用下面的交互作用来探讨系数和程度如何决定多元数值的形状。

  

  INTERACTIVE

  Graphing Polynomials

  

  播放段落
  • Use the sliders to change the leading coefficient  $(a)$  and degree  $\left(n\right)$  .
    ::使用滑动符改变主要系数(a)和程度。
  播放段落
  • Notice how  using the sliders to change the values of   $a$  and   $n$  impacts the shape and position of the graph.
    ::注意使用滑动符改变 n 和 n 的值如何影响图形的形状和位置。
  播放段落
  • Drag the screen to pan and zoom the graph.
    ::拖曳屏幕以调色板并缩放图形。

  
  

  
  

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

  Progress

  0 / 2

  1.

  播放段落

  Complete the table to describe the end behavior rules of polynomials ("up" or "down"):
  ::完成用于描述多面形(“上”或“下”)最终行为规则的表格 :

  	@$\begin{align*}a\end{align*}@$ is positive	@$\begin{align*}a\end{align*}@$ is negative
  degree is even	播放段落 left side: Enter your answer ::左左侧:输入答案 播放段落 right side: Enter your answer ::右侧右侧:输入您的答复	播放段落 left side: Enter your answer ::左左侧:输入答案 播放段落 right side: Enter your answer ::右侧右侧:输入您的答复
  degree is odd	播放段落 left side: Enter your answer ::左左侧:输入答案 播放段落 right side: Enter your answer ::右侧右侧:输入您的答复	播放段落 left side: Enter your answer ::左左侧:输入答案 播放段落 right side: Enter your answer ::右侧右侧:输入您的答复

   

  ---

  播放段落

  Activity 1: End Behavior of Polynomial Graphs
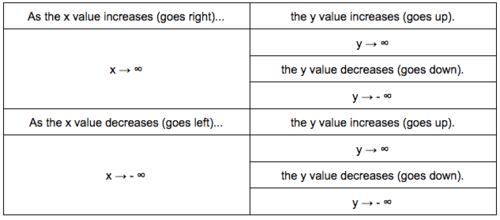
  ::活动1:多面图的结束行为

  播放段落

  In the introduction , the terms “up” and “down” were used to describe the end behavior  of a polynomial function. However, terms like “increases” and “decreases” are more mathematically precise . Additionally, to describe whether a function is increasing or decreasing, you should describe the direction along the $\begin{array}{r}x\text{-}\end{array}$ axis in which you are moving.  To say that the right side of a polynomial points up means that as the $\begin{array}{r}x\text{-}\end{array}$ value increases ( as you go to the right ), the $\begin{array}{r}y\text{-}\end{array}$ value increases (points up).
  ::在导言中,“上”和“下”两词用来描述多边函数的结束行为。然而,“增加”和“减少”等词在数学上更为精确。此外,为了描述一个函数在增加还是减少,您应该描述您移动的 x 轴方向。如果说一个多元点的右侧意味着随着X 值的增加(您向右),Y 值的增加(您向右),y 值的增加( 向上点) 。

  播放段落

  This can also be  stated using mathematical notation.  When the   $\begin{array}{r}x\text{-}\end{array}$ value increases , it is  written as  $\begin{array}{r}x\to \mathrm{\infty }\end{array}$  because it is increasing toward infinity.  When the $\begin{array}{r}x\text{-}\end{array}$ value decreases ,  it is written as  $\begin{array}{r}x\to -\mathrm{\infty }\end{array}$  because it is decreasing toward negative infinity.
  ::也可以用数学符号来表示。 当 x 值增加时, 它被写成 x , 因为它正在向无穷度增长。 当 x 值减少时, 它被写成 x , 因为它正在向负无穷度下降 。

  

  播放段落

  T his notation can be used to write the rules for the end behavior of a polynomial function, as derived in the introduction.
  ::此标记可用于写入导 言中导出的多边函数结束行为的规则 。

  

  播放段落

  Answer the questions  below to practice using these rules.
  ::回答以下使用这些规则的实践问题。

  播放段落

  Discussion Question : Is it possible for a function with an odd degree to have no real roots? Is it possible for a polynomial with an even degree to have no real roots?
  ::讨论问题:具有奇特程度的函数是否可能没有真正的根?具有同等程度的多元婚姻是否可能没有真正的根?

   

  ---

  播放段落

  Activity 2: Multiplicities
  ::活动2:多种用途

  播放段落

  T he previous section, Roots of a Polynomial Equation , introduced zeros of a higher degree polynomial function, representing the x- intercepts , that repeated. T he number of times a zero repeats is referred to using the term multiplicity . Use the interactive below to explore how multiplicity affects a graph.
  ::上一节“多元等式的根”中引入了代表重复的 X 拦截的更高度多元函数的零。重复的零次数是指使用多重性这一术语的次数。使用下面的交互性来探索多重性如何影响一个图形。

  

  INTERACTIVE

  Multiplicities of Polynomials

  

  播放段落
  • See the graph of function,  $f(x) = a(x - 1)(x - 4)^n(x - 7)$  
    
    ::见函数图, f(x) =a(x-1)(x-4)n(x-7)
  播放段落
  • Drag the sliders to change the values of  $a$  and  $n$  
    ::拖动滑动滑动器以更改 n 和 a 的值

  
  

  
  

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

  播放段落
  • When a zero has a multiplicity of 1, the function normally passes through the x-intercept.
    ::当零有多个 1 时,函数通常通过 X 界面。
  播放段落
  • When a zero has a multiplicity of 2, the function bounces off the x-intercept forming a parabola-like shape.
    ::当一个零的多重值为2时,函数会从形成类似抛物线形状的 X 界面中反弹。
  播放段落
  • When a zero has a multiplicity of 3, the function passes through x-intercept, forming a shape that the function  $\begin{array}{r}f(x)=x^3\end{array}$  has. 
    ::当零的多重值为 3 时,函数通过 x 界面,形成函数 f( x) =x3 的形状。

  播放段落

  Make and test a conjecture about how multiplicity relates to the shape formed when the graph passes through the x-intercept.
  ::设定并测试一个猜想,即当图形通过 X 界面时,多重性与形状的形成有何关联。

  播放段落

  Coupl ed  with your knowledge of end behavior, it makes it possible to predict whether the graph of a function will be positive or negative over specific intervals. Use the interactive below to explore another trick to figure this out.
  ::结合你对最终行为的了解, 它可以预测函数的图形是正的还是负的, 在特定的时间间隔内。 使用下面的交互功能来探索另一个技巧来解决这个问题 。

  

  INTERACTIVE

  Positive or Negative over an Interval

  

  播放段落
  • Type a number in the given interval.
    ::在给定间隔中键入数字。
  播放段落
  • Determine whether each factor will be positive or negative when substituting that number for  $x.$  
    ::确定在将数字替换为 x 时,每个因素是正的还是负的。
  播放段落
  • From that, you can determine if that entire interval is positive or negative.
    ::从中,您可以确定整个间隔是正或负。
  播放段落
  • Press "Next Interval" to repeat the process for each interval.
    ::按下“ 下一个间隔” 来重复每个间隔的过程 。

  
  

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

  播放段落

  Answer the questions  below to practice identifying the positivity of a function over intervals defined by the x-intercepts.
  ::回答下述问题,以便从实践上确定一项职能在X调查确定的时间间隔内是否具有积极性。

   

  ---

  播放段落

  Activity 3: Using Characteristics to Graph Polynomial Functions
  ::活动3:在图形多面函数中使用特征

  播放段落

  Use the interactive below to practice graphing polynomial functions using their characteristics.
  ::使用下方的交互功能,使用其特性进行多面函数的图形绘制。

  

  INTERACTIVE

  Finding Polynomials

  

  播放段落
  • Enter the  $x$  values for the roots of the equation in the input box.
    ::在输入框中输入方程式根的 x 值。
  播放段落
  • They will appear on the grid.
    ::他们会出现在网格上
  播放段落
  • Once you have all of the roots, choose the box that the graph would be in based on the interval. 
    ::一旦您拥有了全部根, 请根据间隔选择图形所在的框 。
  播放段落
  • If you get it right, the graph will appear where the box was and you can move to the next interval. 
    ::如果正确的话, 图形将出现在框所在的位置, 您可以移动到下一个间隔 。

  
  

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

   

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题

  播放段落

     Summary
  ::摘要

  播放段落

  For even functions:
  ::对于偶数函数 :

  播放段落
  • If the leading coefficient is positive: as $\begin{array}{r}x\to +\mathrm{\infty },y\to +\mathrm{\infty }\end{array}$  
    ::如果主要系数是正数: as x, y
  播放段落
  • If the leading coefficient is positive: as $\begin{array}{r}x\to -\mathrm{\infty },y\to +\mathrm{\infty }\end{array}$  
    ::如果主要系数是正数: as x, y
  播放段落
  • If the leading coefficient is negative: as $\begin{array}{r}x\to +\mathrm{\infty },y\to -\mathrm{\infty }\end{array}$  
    ::如果主要系数为负: x,y。
  播放段落
  • If the leading coefficient is negative: as $\begin{array}{r}x\to -\mathrm{\infty },y\to -\mathrm{\infty }\end{array}$  
    ::如果主要系数为负: x,y。

  播放段落

  For odd functions:
  ::对于奇数函数 :

  播放段落
  • If the leading coefficient is positive: as $\begin{array}{r}x\to +\mathrm{\infty },y\to +\mathrm{\infty }\end{array}$  
    ::如果主要系数是正数: as x, y
  播放段落
  • If the leading coefficient is positive: as $\begin{array}{r}x\to -\mathrm{\infty },y\to -\mathrm{\infty }\end{array}$  
    ::如果主要系数是正数: as x, y
  播放段落
  • If the leading coefficient is negative: as $\begin{array}{r}x\to +\mathrm{\infty },y\to -\mathrm{\infty }\end{array}$  
    ::如果主要系数为负: x,y。
  播放段落
  • If the leading coefficient is negative: as $\begin{array}{r}x\to -\mathrm{\infty },y\to +\mathrm{\infty }\end{array}$  
    ::如果主要系数为负: x,y。

  播放段落

  The multiplicity is the number of times a factor  appears in the factors of a polynomial.
  ::多重性是多元性因素中一个因素出现的次数。

  播放段落
  • When a zero has a multiplicity of 1, the function passes through the x-intercept.
    ::当零有多个 1 时,函数通过 X 界面。
  播放段落
  • When a zero has a multiplicity of 2, the function bounces off the x-axis at the value of the zero.
    ::当一个零的乘积为2时,函数从X轴反弹,其值为零。
  播放段落
  • When a zero has a multiplicity of 3, the function passes through the x-intercept, forming a shape that the function $\begin{array}{r}f(x)=x^3\end{array}$  has.
    ::当零的多重值为 3 时,函数通过 x 界面,形成函数 f( x) =x3 的形状。