基本绝对值函数

播放段落

While on vacation, you go scuba diving. The surface of the water is at an unknown altitude. You descend to a depth of 90 feet below the surface of the water. What is the vertex of the absolute value function that represents your maximum possible distance from sea level?
::度假时,你去潜水。 水的表面高度未知。 你沉到水表面下方90英尺的深处。 绝对值函数的顶部是什么, 代表你与海平面的最大距离?

播放段落

Graphing Absolute Value Functions
::绝对值函数

播放段落

You  have already learned how to solve and define . N ow take this idea one step further and graph absolute value equations.
::您已经学会了如何解析和定义 。 现在把这个想法再向前一步, 绘制绝对值方程式 。

播放段落

Graphing the Parent Graph of an Absolute Value Function
::绝对值函数的父图形图

播放段落

Let's follow the  steps below to learn about the parent graph of absolute value functions.
::让我们遵循下面的步骤 来了解绝对值函数的母图。

播放段落

Step 1:  G raph $\begin{array}{r}y=|x|\end{array}$ . Draw a table for $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ , with the $\begin{array}{r}x-\end{array}$ values ranging from -3 to 3.
::第1步: 图表 yx 。 绘制 x 和 y 的表格, x - 值介于 - 3 至 3 之间 。

$\begin{array}{r}x\end{array}$	$\begin{array}{r}|x|\end{array}$	$\begin{array}{r}y\end{array}$
$\begin{array}{r}-3\end{array}$	$\begin{array}{r}|-3|\end{array}$	$\begin{array}{r}3\end{array}$
$\begin{array}{r}-2\end{array}$	$\begin{array}{r}|-2|\end{array}$	$\begin{array}{r}2\end{array}$
$\begin{array}{r}-1\end{array}$	$\begin{array}{r}|-1|\end{array}$	$\begin{array}{r}1\end{array}$
	$\begin{array}{r}|0|\end{array}$
$\begin{array}{r}1\end{array}$	$\begin{array}{r}|1|\end{array}$	$\begin{array}{r}1\end{array}$
$\begin{array}{r}2\end{array}$	$\begin{array}{r}|2|\end{array}$	$\begin{array}{r}2\end{array}$
$\begin{array}{r}3\end{array}$	$\begin{array}{r}|3|\end{array}$	$\begin{array}{r}3\end{array}$

播放段落

Step 2: Recall that the absolute value of a number is always positive. P lot each of the seven coordinate pairs  and graph the function.
::步骤2:回顾一个数字的绝对值总是正数。绘制七个坐标对中的每一个,并绘制函数图。

播放段落

Step 3: Notice that this function is very similar to the linear function , $\begin{array}{r}y=x\end{array}$ . Draw this line on the graph in a different color or with a dashed line.
::第3步:注意此函数与 y=x 线性函数非常相似。 在图形上以不同颜色或破折线绘制此线条。

播放段落

Step 4: Now, fold the  graph on the $\begin{array}{r}x-\end{array}$ axis. What do you notice?
::第4步:现在,折叠 X - 轴上的图表。你注意到什么了?

播放段落

Y ou should notice  that when you fold your graph on the $\begin{array}{r}x-\end{array}$ axis, the line $\begin{array}{r}y=x\end{array}$ becomes the absolute value equation  $\begin{array}{r}y=|x|\end{array}$ . That is because the absolute value of a number can never be below zero; therefore the range will always be positive.  $\begin{array}{r}y=|x|\end{array}$  is considered the parent graph because it is the most basic of all the absolute value functions. All linear absolute value functions have this “V” shape.
::您应该注意到, 当您在 x - 轴折叠您的图形时, 线 y=x 将变成绝对值方程式 y x 。 这是因为数字的绝对值永远不能低于零; 因此, 范围将永远是正的。 y x 将被视为母图, 因为它是所有绝对值函数中最基本的函数。 所有线性绝对值函数都具有此“ V” 形状 。

播放段落

In general, you  can define the graph of $\begin{array}{r}y=|x|\end{array}$ as $\begin{array}{r}y=\{\begin{array}{ll}x;& x\ge 0\\ -x;& x<0\end{array}\end{array}$ . E ach side is the mirror image of the other, over a vertical line through the vertex.
::一般而言,您可以将 yx 的图形定义为 yx;x0-x;x<0。 每一面都是另一面的镜像, 穿过顶端的垂直线。

播放段落

Now, let's use a table to graph the following functions.
::现在,让我们用一个表格来绘制以下函数的图形。

播放段落
1. Graph $\begin{array}{r}y=|x-3|\end{array}$ . Determine the domain and range.
   ::图形 yx-3. 确定域和范围。

播放段落

In general, when you use a table to graph a function, pick some positive and negative numbers, as well as zero. Use the equation to help you determine which $\begin{array}{r}x-\end{array}$ values to pick. Setting what is inside the absolute value equal to zero yields  $\begin{array}{r}x=3\end{array}$ . Pick three values on either side of $\begin{array}{r}x=3\end{array}$ and then graph.
::一般而言,当您使用表格来绘制函数时,请选择一些正数和负数,以及零。使用方程式来帮助您确定要选择的 x- 值。设置绝对值内值等于零收益x=3。在 x=3 的两侧选择三个值,然后绘制图形。

$\begin{array}{r}x\end{array}$	$\begin{array}{r}|x-3|\end{array}$	$\begin{array}{r}y\end{array}$
0	$\begin{array}{r}|-3|\end{array}$	3
1	$\begin{array}{r}|-2|\end{array}$	2
2	$\begin{array}{r}|-1|\end{array}$	1
3	$\begin{array}{r}|0|\end{array}$	0
4	$\begin{array}{r}|1|\end{array}$	1
5	$\begin{array}{r}|2|\end{array}$	2
6	$\begin{array}{r}|3|\end{array}$	3

播放段落

Notice that this graph shifts to the right 3 when compared to the parent graph. The domain will be all real numbers, $\begin{array}{r}x\in \mathbb{R}\end{array}$ , and the range will be all positive real numbers, including zero, $\begin{array}{r}y\in [0,\mathrm{\infty }).\end{array}$
::请注意, 此图表与父图形比较时向右移到右 3 。 域名将全部为真实数字 xR, 范围将全部为正数, 包括零, y_ {0} 。

播放段落
2. G raph $\begin{array}{r}y=|x|-5\end{array}$ . Determine the domain and range.
   ::5. 确定域域和范围。

播放段落

Be careful! Here, the minus 5 is not inside the absolute value. So, first take the absolute value of the $\begin{array}{r}x-\end{array}$ value and then subtract 5. In cases like these, where a value is subtracted after taking the absolute value,  the range may include negative numbers.
::注意! 在这里, 负 5 不在绝对值之内。 所以, 首先取 x- value 的绝对值, 然后减去 5 。 在这样的情况下, 如果在计算绝对值后减去一个数值, 则范围可能包括负数 。

$\begin{array}{r}x\end{array}$	$\begin{array}{r}|x|-5\end{array}$	$\begin{array}{r}y\end{array}$
$\begin{array}{r}-3\end{array}$	$\begin{array}{r}|-3|-5\end{array}$	$\begin{array}{r}-2\end{array}$
$\begin{array}{r}-2\end{array}$	$\begin{array}{r}|-2|-5\end{array}$	$\begin{array}{r}-3\end{array}$
$\begin{array}{r}-1\end{array}$	$\begin{array}{r}|-1|-5\end{array}$	$\begin{array}{r}-4\end{array}$
	$\begin{array}{r}|0|-5\end{array}$	$\begin{array}{r}-5\end{array}$
$\begin{array}{r}1\end{array}$	$\begin{array}{r}|1|-5\end{array}$	$\begin{array}{r}-4\end{array}$
$\begin{array}{r}2\end{array}$	$\begin{array}{r}|2|-5\end{array}$	$\begin{array}{r}-3\end{array}$
$\begin{array}{r}3\end{array}$	$\begin{array}{r}|3|-5\end{array}$	$\begin{array}{r}-2\end{array}$

播放段落

Here, the graph shifts down 5 when compared to the parent graph. The domain will be all real numbers, $\begin{array}{r}x\in \mathbb{R}\end{array}$ , and the range will be all real numbers greater than or equal to -5, $\begin{array}{r}y\in [\text{-}5,\mathrm{\infty }).\end{array}$
::这里, 图形与父图形相比向下移动 5 。 域将全部为真实数字 xR, 区域将全部为实际数字大于或等于 5 y y y {-5} 。

播放段落

In these t wo absolute value graphs, you may have noticed that there is a minimum point. This point is called the vertex. For instance , in the previous problem, the vertex is (0, -5). The vertex can also be a maximum. See the next  problem.
::在这两个绝对值图形中,您可能注意到有一个最小点。这个点被称为顶点。例如,在上一个问题中,顶点为 0, - 5。顶点也可以是一个最大值。请看下一个问题。

播放段落
3. Use a table to graph $\begin{array}{r}y=-|x-1|+2.\end{array}$  Determine the vertex, domain, and range.
   ::使用表格绘制 yx- 12. 确定顶点、 域和范围 。

播放段落

Determine the  $\begin{array}{r}x\end{array}$ -value that  makes the inside of the absolute value equation zero  $\begin{array}{r}(x=1)\end{array}$ . Then make a table of values, including a couple values on either side of that $\begin{array}{r}x\end{array}$ -value.
::确定使绝对值方程式零(x=1)内部成为绝对值方程式零(x=1)的 x 值,然后绘制一个数值表,包括该X 值两侧的一对数值。

$\begin{array}{r}x\end{array}$	$\begin{array}{r}-|x-1|+2\end{array}$	$\begin{array}{r}y\end{array}$
-2	$\begin{array}{r}-|-2-1|+2\end{array}$	-1
-1	$\begin{array}{r}-|-1-1|+2\end{array}$	0
0	$\begin{array}{r}-|0-1|+2\end{array}$	1
1	$\begin{array}{r}-|1-1|+2\end{array}$	2
2	$\begin{array}{r}-|2-1|+2\end{array}$	1
3	$\begin{array}{r}-|3-1|+2\end{array}$	0
4	$\begin{array}{r}-|4-1|+2\end{array}$	-1

播放段落

The vertex is (1, 2) and in this case, it is the maximum value. The domain is $\begin{array}{r}x\in \mathbb{R}\end{array}$ , and the range is $\begin{array}{r}y\in (-\mathrm{\infty },2].\end{array}$
::顶点是(1, 2) , 在此情况下, 是最大值 。 域是 xR, 范围是 y( , 2) 。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were asked to identify the vertex of an  absolute value function that represents your possible distance from sea level after diving.
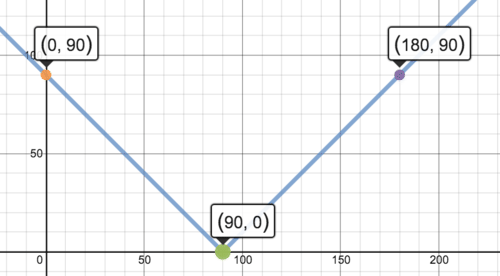
::早些时候,有人要求你确定 绝对值函数的顶点 代表你潜入后 可能距离海平面的距离

播放段落

The absolute value function that represents this situation is  $\begin{array}{r}y=\left|x-90\right|,\end{array}$ where  $\begin{array}{r}x\end{array}$  is your altitude above or below  sea level before diving. By graphing this function, you can see that the vertex occurs at the point (90, 0).
::表示此状态的绝对值函数是 yx- 90 , x 是潜水前海平面以上或以下的高度。 通过图形化此函数, 您可以看到顶点( 90, 0) 发生于点( 90, 0) 。

播放段落

Example 2
::例2

播放段落

Graph $\begin{array}{r}y=\text{-}\left|x-5\right|\end{array}$  using a table. Determine the vertex, domain, and range.
::使用表格确定顶点、域和范围。

播放段落

Determine what makes the inside of the absolute value equation zero, $\begin{array}{r}x=5\end{array}$ . Then, to make a  table of values, pick a couple values on either side of $\begin{array}{r}x=5\end{array}$ .
::确定绝对值零的内值, x=5 。 然后,要绘制一个数值表,请在 x=5 的两侧选择一对数值。

$\begin{array}{r}x\end{array}$	$\begin{array}{r}-|x-5|\end{array}$	$\begin{array}{r}y\end{array}$
2	$\begin{array}{r}-|2-5|\end{array}$	-3
3	$\begin{array}{r}-|3-5|\end{array}$	-2
-4	$\begin{array}{r}-|4-5|\end{array}$	-1
5	$\begin{array}{r}-|5-5|\end{array}$	0
6	$\begin{array}{r}-|6-5|\end{array}$	-1
7	$\begin{array}{r}-|7-5|\end{array}$	-2
8	$\begin{array}{r}-|8-5|\end{array}$	-3

播放段落

The vertex is (5, 0) and in this case, it is the maximum value. The domain is $\begin{array}{r}x\in \mathbb{R}\end{array}$ , and the range is $\begin{array}{r}y\in (-\mathrm{\infty },0].\end{array}$
::顶点是 (5, 0) , 在此情况下, 是最大值 。 域是 xR, 范围是 y( , 0) 。

播放段落

Example 3
::例3

播放段落

Use a table to graph $\begin{array}{r}y=\left|x+4\right|-2.\end{array}$  Determine the vertex, domain, and range.
::使用表格绘制 yx+42. 确定顶点、 域和范围 。

播放段落

Determine what makes the inside of the absolute value equation zero, $\begin{array}{r}x=-4\end{array}$ . Then make a  table of values, including  a couple values on either side of $\begin{array}{r}x=-4\end{array}$ .
::确定绝对值零的内值, x4。 然后绘制一个数值表, 包括 x4 的两面的数值 。

$\begin{array}{r}x\end{array}$	$\begin{array}{r}|x+4|-2\end{array}$	$\begin{array}{r}y\end{array}$
$\begin{array}{r}-1\end{array}$	$\begin{array}{r}|-1+4|-2\end{array}$	1
-2	$\begin{array}{r}|-2+4|-2\end{array}$	0
-3	$\begin{array}{r}|-3+4|-2\end{array}$	-1
-4	$\begin{array}{r}|-4+4|-2\end{array}$	-2
-5	$\begin{array}{r}|-5+4|-2\end{array}$	-1
-6	$\begin{array}{r}|-6+4|-2\end{array}$	0
-7	$\begin{array}{r}|-7+4|-2\end{array}$	1

播放段落

The vertex is (-4, -2) and in this case, it is the minimum value. The domain is $\begin{array}{r}x\in \mathbb{R}\end{array}$ , and the range is $\begin{array}{r}y\in [-2,\mathrm{\infty }).\end{array}$
::顶点是 (4, 4, 2) , 在此情况下, 这是最小值 。 域是 x R, 范围是 y [ - 2, ] 。

播放段落

Review
::回顾

播放段落

Graph the following functions using a table. Determine the vertex, domain, and range of each function.
::用表格绘制以下函数的图。确定每个函数的顶点、域和范围。

播放段落
1. $\begin{array}{r}y=|x+6|\end{array}$
   ::yx+6________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
播放段落
2. $\begin{array}{r}y=|x-4|\end{array}$
   ::~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
播放段落
3. $\begin{array}{r}y=-|x|+3\end{array}$
   ::yx3
播放段落
4. $\begin{array}{r}y=|x|-2\end{array}$
   ::y'x%2
播放段落
5. $\begin{array}{r}y=-|x+3|+7\end{array}$
   ::yx+3+7
播放段落
6. $\begin{array}{r}y=|x-1|-6\end{array}$
   ::yx - 16
播放段落
7. $\begin{array}{r}y=2|x|\end{array}$
   ::y=2x
播放段落
8. $\begin{array}{r}y=-3|x|\end{array}$
   ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
播放段落
9. $\begin{array}{r}y=\frac{1}{3}|x|\end{array}$
   ::y=13=x*}Y=13=x*}Y=13=x*}Y=13=x*}Y=13=x*}Y=13=x*

播放段落

Reference  problems 1-9 as needed to fill in the blanks in problems 10-15.
::需要参考问题1-9,以填补问题10-15中的空白。

播放段落
10. If there is a negative sign in front of the absolute value, the graph is ________________ (when compared to the parent graph).
    ::如果绝对值前面有一个负符号,则图表为 _______(与母图比较时)。
播放段落
11. If the equation is $\begin{array}{r}y=|x-h|+k\end{array}$ , the vertex will be ___________________.
    ::如果等式是yx-hk,顶点将是。
播放段落
12. The domain of an absolute value function is always ____________________________.
    ::绝对值函数的域始终是 {} {} 。
播放段落
13. For $\begin{array}{r}y=a|x|\end{array}$ , if $\begin{array}{r}a>1\end{array}$ , then the graph will be ___________________ than the parent graph.
    ::对于 y=ax, 如果 a>1, 则图形将比 父图形为 \\\ 。
播放段落
14. For $\begin{array}{r}y=a|x|\end{array}$ , if $\begin{array}{r}0<a<1\end{array}$ , then the graph will be ___________________ than the parent graph.
    ::y=ax,如果 0<a<1, 则图形将比父图形为 \\\\ 。
播放段落
15. Without making a table, what is the vertex of $\begin{array}{r}y=\left|x-9\right|+7?\end{array}$
    ::不做桌子,你-9-7的顶点是什么?

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。