16.2 答复 -- -- 第2章:函数和图表

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 答复 - Ch 2:函数和图表

  Collapse Expand

  答复 - Ch 2:函数和图表

  播放段落

  Section 2.2: Domain and Range
  ::第2.2节:面积和范围

  播放段落
  1. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-} \infty, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}[\text{-}1, 1]\end{align*}$  
     ::域 : x (- , ) 范围 : y [-1, 1]
  播放段落
  2. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-} \infty, 2) \cup{} [3, \infty)\end{align*}$    Range: $\begin{align*}y\end{align*}$ ∈  $\begin{align*}[\text{-}8, \infty)\end{align*}$  
     ::域 : x
  播放段落
  3. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-} \infty, \infty)\end{align*}$   Range: $\begin{align*}y\end{align*}$ ∈  $\begin{align*}[0, 2]\end{align*}$  
     ::域 : x (- , ) 范围 : y [0, 2]
  播放段落
  4. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-} \infty, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}[\text{-}3, \infty)\end{align*}$  
     ::域 : x (- , ) 范围 : y [-3, ]
  播放段落
  5. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-} \infty, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}(\text{-}\infty, 2]\end{align*}$  
     ::域 : x (- , ) 范围 : y (- , 2)
  播放段落
  6. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-} \infty, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}(\text{-}1, \infty)\end{align*}$  
     ::域 : x (- , ) 范围 : y (-1, )
  播放段落
  7. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-}3, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}(\text{-} \infty, \infty)\end{align*}$
     ::域 : x (3, ) 域 : y (- , )
  播放段落
  8. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}\left\{\text{-}2, \tfrac{3}{4}, \tfrac{\pi}{2}, 2, 3\right\}\end{align*}$  Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}\left\{1, \pi, 5, 7\right\}\end{align*}$  
     ::域 : x { { 2, 34, 2, 2, 3} 范围 : y { { 1, , 5,7}
  播放段落
  9. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-} \infty, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}(\text{-}\infty, 4]\end{align*}$  
     ::域 域 : x (- , ) 域 : y (- , ) 4
  播放段落
  10. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}\left(\tfrac{1}{2}, \infty \right)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}(\text{-} \infty, \infty)\end{align*}$
      ::域 : x (12, ) 范围 : y (-, , )
  播放段落
  11. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-}\infty, 1) \cup (1, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}(\text{-}\infty, 0) \cup (0, \infty)\end{align*}$  
      ::域 : x (- , 1, ) (1, ) 范围 : y (- , 0) (0, ) 。
  播放段落
  12. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}[\text{-}4, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}(\text{-}\infty, \text{-}1]\end{align*}$  
      ::域 : x [ 4 ] 范围 : y (- , -1)
  播放段落
  13. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-}\infty, \text{-}6) \cup (\text{-}6, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}(\text{-}\infty, \text{-}1) \cup (\text{-}1, \infty)\end{align*}$  
      ::域 : x (- , , , , , , , , , ) 范围 : y (- , , , , , , , , , ) 范围 : y (- , , , , , )
  播放段落
  14. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-}\infty, \text{-}1) \cup (1, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}(\text{-} \infty, \infty)\end{align*}$
      ::域 : x (- ,-1, ) 域 : y (- , )
  播放段落
  15. Domain:  $\begin{align*}x\end{align*}$  ∈  $\begin{align*}(\text{-}\infty, \text{-}1.5] \cup [1.5, \infty)\end{align*}$   Range:  $\begin{align*}y\end{align*}$ ∈  $\begin{align*}[6, \infty)\end{align*}$  
      ::域 : x (- ,- 1.5] [1.5, ] 范围 : y [6, ]
  播放段落
  16. The independent variable is  $\begin{align*}h\end{align*}$ , the hours he worked. Domain: $\begin{align*}x\end{align*}$  ∈  $\begin{align*}[20, 25]\end{align*}$   Range: $\begin{align*}y\end{align*}$ ∈  $\begin{align*}[200, 250]\end{align*}$  
      ::独立的变量是h, 他工作的时间。 域 : x [ 20, 25] 范围 : y [ 200, 250]
  播放段落
  17. Domain: $\begin{align*}x\end{align*}$  ∈  $\begin{align*}[10, 12]\end{align*}$   Range: $\begin{align*}y\end{align*}$ ∈  $\begin{align*}[300, 360]\end{align*}$   She can drive between 300 and 360 miles.
      ::域 : x [10,12] 范围 : y [300,360] 她可以驾驶300至360英里。
  播放段落
  18. Domain: $\begin{align*}x\end{align*}$  ∈  $\begin{align*}[4, 8]\end{align*}$   Range: $\begin{align*}y\end{align*}$ ∈  $\begin{align*}[11, 22]\end{align*}$   The evening cost between $11 and $22.
      ::域: x [4,8] 范围: y [11,22] 晚间费用在11美元至22美元之间。

  播放段落

  Section 2.3: Maximums and Minimums
  ::第2.3节:最高和最低

  播放段落
  1. There is a global minimum at (3, 0).
     ::全球最低值(3 0)为全球最低值。
  播放段落
  2. There  is a local minimum at (3, 0).
     ::当地最低限额为3 0。
  播放段落
  3. Global minimum at  $\begin{align*}\left(\text{-}\tfrac{\pi}{2}, \text{-}1\right)\!,\end{align*}$  and global maximum at $\begin{align*}\left(\tfrac{\pi}{2}, 1\right)\end{align*}$
     ::全球最低值(-__2,-1),全球最高值(-2,-1),全球最高值(-2,1)
  播放段落
  4. Local minimum at  $\begin{align*}\left(\text{-}\tfrac{\pi}{2}, \text{-}1\right)\!,\end{align*}$  and local maximum at  $\begin{align*}\left(\tfrac{\pi}{2}, 1\right)\end{align*}$
     ::当地最低值(-%2,-1),当地最高值(-%2,-1),当地最高值(-%2,1)
  播放段落
  5. There are no global extrema.
     ::没有全球极端现象。
  播放段落
  6. There are no local extrema.
     ::当地没有直径。
  播放段落
  7. There are no global extrema.
     ::没有全球极端现象。
  播放段落
  8. Local minimums: (0.4, -1), (2.5, -13). Local maximums: (-1.5, 22), (1, 0). [Note: Points are approximate.]
     ::当地最低数值0.4)-1,(2.5,-13),当地最高数值-1.5,22),(1,0),[注:要点大致相同。 ]
  播放段落
  9. There are no global extrema.
     ::没有全球极端现象。
  播放段落
  10. Local minimum: (3, 0). Local maximum: (0.5, 9.5). [Note: Points are approximate.]
      ::当地最低比率3 0) 当地最高比率0.5,9.5) [注:要点大致相同。 ]
  播放段落
  11. A global maximum is the overall highest point on the graph, while the local maximum is the highest point within a certain neighborhood of the graph.
      ::全球最大值是图中的总最高点,而本地最高值是图中某个区域的最高点。
  播放段落
  12. Answers vary. Graph should show a global minimum, a local maximum, and no global maximum. (There can be a local minimum.)
      ::答案各有不同。图表应显示全球最低值、地方最高值、全球最高值。 (当地最低值可以是当地最低值。 )
  播放段落
  13. Answers vary. Graph should have no global extrema, but both types of local extrema.
      ::答案各有不同。图中不应有全球性的外形,但两种类型的局部外形。
  播放段落
  14. Local maximum: (-1.16, 36.24). Local minimum: (-4, 0). No global maximum. Global minimum: (2,16, -18.49).
      ::当地最高额-1.16, 36.24) 当地最低额4, 0) 全球最高额; 全球最低额2,16, 18.49)。
  播放段落
  15. Local maximum: (-1,0). Local minimum: (0.22, -3.23). Global maximum: (2.28, 9.91). No global minimum.
      ::当地最高值-1,0)当地最低值0.22,-3.23)全球最高值2.28,9.91)没有全球最低值。
  播放段落
  16. A length and width of approximately 4.472 will minimize the perimeter. The perimeter would be approximately 17.889 inches.
      ::长度和宽度约为4.472,将最大限度地缩小周界,周界约为17.889英寸。
  播放段落
  17. $\begin{align*}A = w\cdot \left(\tfrac{P-2w}{2}\right) \ \text{or} \ A = \text{-}w^2 + \tfrac{1}{2}Pw.\end{align*}$  The rectangle with the maximum area would be the one where the width is 1/4 of the perimeter.
      ::A=w(P- 2w2) 或 A=-w2+12Pw。 最大面积的矩形将是宽度为周界四分之一的矩形。
  播放段落
  18.  800 square feet
      ::800平方英尺

   

  播放段落

  Section 2.4: Symmetry
  ::第2.4节:对称

  播放段落
  1. Even
     ::偶偶偶
  播放段落
  2. Odd
     ::奇数
  播放段落
  3. Neither
     ::中 无
  播放段落
  4. Neither
     ::中 无
  播放段落
  5. Odd
     ::奇数
  播放段落
  6. Neither
     ::中 无
  播放段落
  7. Neither
     ::中 无
  播放段落
  8. Even
     ::偶偶偶
  播放段落
  9.   $\begin{align*}f(\text{-}x) = h(\text{-}x)-g(\text{-}x) = h(x) + g(x) \ne f(x) \ \mathrm{or} \ \text{-}f(x)\end{align*}$
     :f-x) =h(-x) -g(-x) =h(x) +g(x) +g(x) f(x) 或-f(x)
  播放段落
  10.   $\begin{align*}f(\text{-}x) = \frac{h(\text{-}x)}{g(\text{-}x)} = \text{-}\frac{h(x)}{g(x)} = \text{-}f(x)\end{align*}$
      :f-x)=h(x)g(x)=-h(x)g(x)=-h(x)g(x)g(x)=-f(x)
  播放段落
  11.   $\begin{align*}f(\text{-}x) = h(\text{-}x)g(\text{-}x) = \text{-}h(x)g(x) = \text{-}f(x)\end{align*}$
      :f-x)=h(x)g(x)=-h(x)g(x)=-h(x)g(x)g(x)=-f(x)
  播放段落
  12. Yes. If $\begin{align*}h(x)\end{align*}$  and $\begin{align*}g(x)\end{align*}$  are both even and $\begin{align*}f(x)=\end{align*}$   $\begin{align*}h(x)+g(x)\end{align*}$ , then  $\begin{align*}f(-x)=h(-x)+g(-x)\end{align*}$ $\begin{align*}=h(x)+g(x)=f(x)\end{align*}$ .
      ::是。如果 h(x) 和 g(x) 是偶数 和 f(x) = h(x)+g(x),那么 f(x) = h(x) = h(x) +g(x) = h(x) = h(x)+g(x) = h(x)+g(x)= f(x)。
  播放段落
  13. Yes. If $\begin{align*}h(x)\end{align*}$  and $\begin{align*}g(x)\end{align*}$  are both odd and $\begin{align*}f(x)=h(x)+g(x)\end{align*}$ , then  $\begin{align*}f(-x)=h(-x)+g(-x)=-h(x)-g(x)=-[h(x)+g(x)]=-f(x)\end{align*}$  
      ::是 。 如果 h( x) 和 g( x) 既为奇数, 且 f( x) = h( x) +g( x) , 那么 f( x) = h( x) = h( x) +g( - x) +g( x) - x) \ (x) \ (x) \ [h( x) +g( x)]\ f( x)
  播放段落
  14. There are some functions that do not have reflection symmetry across the $\begin{align*}y\end{align*}$ -axis, or rotation symmetry about the origin.
      ::有一些函数在 Y 轴之间没有反射对称,或者对原值没有旋转对称。
  播放段落
  15. If a function is even, then it is symmetrical across the $\begin{align*}y\end{align*}$ -axis. If a function is odd, then it has rotation symmetry about the origin.
      ::如果函数是偶数,则在 Y 轴之间对称。如果函数是奇数,则会对原值进行旋转对称。

   

  播放段落

  Section 2.5: Increasing and Decreasing
  ::第2.5节:增加和减少

  播放段落
  1. Increasing:  $\begin{align*}x\end{align*}$  ∈ (3, $\begin{align*}\infty \end{align*}$ )
     ::增加: x (3, )
  播放段落
  2. Decreasing:  $\begin{align*}x\end{align*}$  ∈ ( $\begin{align*}\text{-}\infty \end{align*}$ ,3)
     ::下降: x (- , 3)
  播放段落
  3. Increasing:  $\begin{align*}x\end{align*}$  ∈ ( $\begin{align*}\text{-}\frac{\pi }{2}\end{align*}$ , $\begin{align*}\frac{\pi }{2}\end{align*}$ )
     ::增加: x (- 2, 2)
  播放段落
  4. Decreasing:  $\begin{align*}x\end{align*}$  ∈ ( $\begin{align*}\text{-}\pi \end{align*}$ , $\begin{align*}\frac{\pi }{2}\end{align*}$ ) ∪ ( $\begin{align*}\frac{\pi }{2}\end{align*}$ , $\begin{align*}\pi \end{align*}$ )
     ::下降: x (- , 2) ( 2, )
  播放段落
  5. Increasing:  $\begin{align*}x\end{align*}$  ∈ ( $\begin{align*}\text{-}\infty \end{align*}$ , $\begin{align*}\infty \end{align*}$ )
     ::增加: x (- , )
  播放段落
  6. None
     ::无无无无无无无
  播放段落
  7. Increasing:  $\begin{align*}x\end{align*}$ ∈ ( $\begin{align*}\text{-}\infty \end{align*}$ , -1.4) ∪ (0.3, 1) ∪ (2.5,  $\begin{align*}\infty \end{align*}$ ) [Note: Points are approximate.]
     ::增加: x (- , - 1.4) (0.3, 1) (2.5, ) [注:要点大致相同。 ]
  播放段落
  8. Decreasing:  $\begin{align*}x\end{align*}$  ∈ (-1.4, 0.3) ∪ (1, 2.5) [Note:  P oints are approximate.]
     ::下降: x (1.4, 0.3) (1, 2.5) [注:要点大致相同。 ]
  播放段落
  9. Increasing:  $\begin{align*}x\end{align*}$  ∈ (- $\begin{align*}\infty \end{align*}$ , 0.3) ∪ (3,  $\begin{align*}\infty \end{align*}$ )
     ::增加: x (- , 0. 3) (3, )
  播放段落
  10. Decreasing:  $\begin{align*}x\end{align*}$  ∈ (0.3, 3)
      ::下降: x (0.3, 3)
  播放段落
  11. Answers vary. [Possible answer: A line with a positive slope.]
      ::[可能的答案:正斜坡线。 ]
  播放段落
  12. Answers vary. [Possible answer: A line with a negative slope.]
      ::[可能的答案:负斜度线。 ]
  播放段落
  13. Increasing: $\begin{align*}x\end{align*}$  ∈ (- $\begin{align*}\infty \end{align*}$ , 1) ∪ (3,  $\begin{align*}\infty \end{align*}$ ) & Decreasing: $\begin{align*}x\end{align*}$  ∈ (1, 3)
      ::递增: x (- , 1) (3, ) 和 递减: x (1, 3)
  播放段落
  14. Increasing: $\begin{align*}x\end{align*}$  ∈ (- $\begin{align*}\infty \end{align*}$ , 1) & Decreasing: $\begin{align*}x\end{align*}$  ∈ (1,  $\begin{align*}\infty \end{align*}$ )
      ::递增: x (- , 1) 和 递减: x (1, ) (1, )
  播放段落
  15. Increasing: $\begin{align*}x\end{align*}$  ∈ (5, $\begin{align*}\infty \end{align*}$ ) & Decreasing: $\begin{align*}x\end{align*}$ ∈ (- $\begin{align*}\infty \end{align*}$ , 5)
      ::增加: x (5, ) 和 减少: x (- , 5)
  播放段落
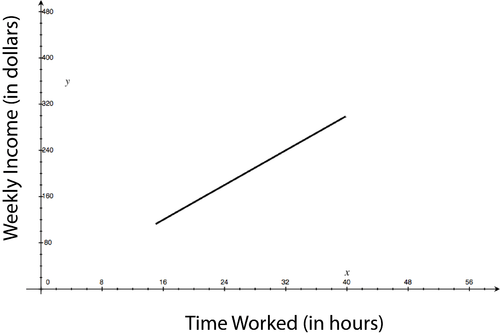
  16. Extrema are at (15, 112.5) and (40, 300).
      
      
      ::异常值为(15,112.5)和(40,300)。
  播放段落
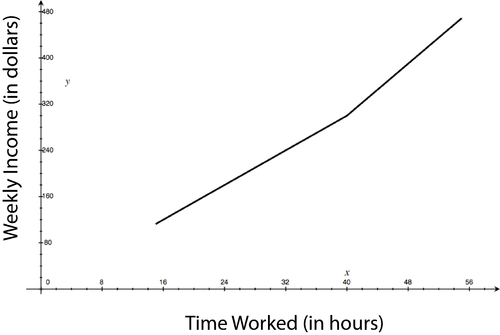
  17. Max value changes if he works overtime. The new extrema are (15, 112.5) and (55, 468.75).
      ::如果他加班,最大值会变化。新的外形是(15,112.5)和(55,468.75)。
  播放段落
  18. Extrema are (15, 112.5) and (55, 468.75).
      
      
      ::异端是(15,112.5)和(55,468.75)。

   

  播放段落

  Section 2.6: Intercepts of Graphs of Functions
  ::第2.6节:职能图图的截断

  播放段落
  1.   $\begin{align*}y\end{align*}$ -intercept: (0, -4); Zeroes: (-1,0) and (4, 0) 
     ::y 拦截: (0, - 4); 零1,0)和(4,0)
  播放段落
  2.   $\begin{align*}y\end{align*}$ -intercept: (0, -12); Roots: (-3,0), (1,0), and (2, 0)
     ::y 拦截: (0, - 12); 根 30,0, 1,0) 和(2, 0)
  播放段落
  3.   $\begin{align*}y\end{align*}$ -intercept is approximately (0, 6), $\begin{align*}x\end{align*}$ -intercepts are (-2,0) and (1, 0)
     ::y 拦截大约为( 0, 6), x 拦截是( 2, 0) 和(1, 0)
  播放段落
  4. Both $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ - intercepts are at (0,0).
     ::X 和 y 的界面都在 0,0 。
  播放段落
  5. Both $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -intercepts are at (0,0).
     ::X 和 y 的界面都在 0,0 。
  播放段落
  6. No $\begin{align*}y\end{align*}$ -intercept; $\begin{align*}x\end{align*}$ -intercept is (1, 0).
     ::没有 y 界面; x 界面是 1, 0 。
  播放段落
  7. No $\begin{align*}x\end{align*}$ - or $\begin{align*}y\end{align*}$ -intercepts
     ::无 x 或 Y 界面
  播放段落
  8.   $\begin{align*}y\end{align*}$ -intercept is (0, 1); no $\begin{align*}x\end{align*}$ -intercept
     ::y 界面是 (0, 1); 没有 x 界面
  播放段落
  9. Both $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -intercepts are (0,0).
     ::X 和 y 界面为 0,0 。
  播放段落
  10. Yes, because there are functions that are undefined when $\begin{align*}x=0\end{align*}$ .
      ::是, 因为有函数在 x=0 时未定义 。
  播放段落
  11. Yes, because there are functions with no real solutions when $\begin{align*}y=0\end{align*}$ .
      ::是的, 因为有函数在 y=0 时没有真正的解决方案 。
  播放段落
  12. The $\begin{align*}x\end{align*}$ -intercept of  $\begin{align*}f(x)\end{align*}$  is called a zero because it is the solution to $\begin{align*}f(x)=0\end{align*}$ .
      ::f( x) 的 x interview 被称为 0 , 因为它是 f( x) = 0 的解决方案 。
  播放段落
  13.   $\begin{align*}y\end{align*}$ -intercept: (0, 10); $\begin{align*}x\end{align*}$ -intercepts: (2,0), (-1,0), (5,0)
      ::y 拦截: (0, 10); x 拦截: (2,0), (1,0), (5,0)
  播放段落
  14.   $\begin{align*}y\end{align*}$ -intercept: (0, -7); $\begin{align*}x\end{align*}$ -intercepts: (-1,0), (7,0)
      ::y 拦截0, - 7); x 拦截1,0),(7,0)
  播放段落
  15.   $\begin{align*}y\end{align*}$ -intercept: (0, 5); $\begin{align*}x\end{align*}$ -intercepts: (5,0), (-1/2, 0), (1,0)
      ::y 拦截: (0, 5); x 拦截: (5,0), (1, 2, 0), (1,0)

    

  播放段落

  Section 2.7: Function Families 
  ::第2.7节:功能家庭

  播放段落
  1. $\begin{align*}y={b}^{x}\end{align*}$  
     
     ::y=bx y=bx
  播放段落
  2. $\begin{align*}y=\log_{b}{x}\end{align*}$  
     
     ::y=logbx y=logbx y=logbx logbx y=logbx logbx y=logbx y=logbx logbx y=logbx y=logbx y=logbx logbx y=logbx y=logbx y=logbx y=logbx
  播放段落
  3. $\begin{align*}y=\sin{x}\end{align*}$  
     
     ::y=sinx y=sinx y=sinx y=sinx y=inx y=sinx y=sinx y=sinx y=sinx y=sinx y=sinx y=sinx
  播放段落
  4. $\begin{align*}y={x}^{2}\end{align*}$  
     
     ::y=x2 y=x2
  播放段落
  5. $\begin{align*}y= \left|x\right|\end{align*}$  
     
     ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
  播放段落
  6. $\begin{align*}y=\tfrac{1}{x}\end{align*}$  
     
     ::y=1x y=1x
  播放段落
  7. $\begin{align*}y=\tfrac{1}{1+{b}^{\text{-}x}}\end{align*}$  
     
     ::y=11+b-x y=11+b-x
  播放段落
  8. $\begin{align*}y=\sqrt{x}\end{align*}$  
     
     ::yx
  播放段落
  9. $\begin{align*}y={x}^{3}\end{align*}$  
     
     ::y=x3 y=x3
  播放段落
  10. $\begin{align*}y=x\end{align*}$  
      
      ::y=x y=x
  播放段落
  11.   $\begin{align*}y=\tfrac{1}{x}\end{align*}$  because  $\begin{align*}\tfrac{1}{0}\end{align*}$  is undefined.
      ::y=1x 因为 10 未定义 。
  播放段落
  12.   $\begin{align*}y={e}^{x}\!,\end{align*}$   $\begin{align*}y={x}^{2}\!,\end{align*}$    $\begin{align*}y=\sqrt{x},\!\end{align*}$    $\begin{align*}y=\left|x\right|\end{align*}$   
      ::y=ex,y=x2,y=x,y=xx,y=xx
  播放段落
  13. One difference is  $\begin{align*}y={x}^{2}\end{align*}$   has a minimum value, while  $\begin{align*}y={x}^{3}\end{align*}$  doesn't.
      ::一个差异是 Y=x2 有最小值, 而 y=x3 没有 。
  播放段落
  14. The two graphs are reflections of one another across the line  $\begin{align*}y=x\end{align*}$ .
      ::这两个图表是横跨y=x线的相互反射。
  播放段落
  15.   $\begin{align*}y=\sqrt{x}\end{align*}$   is not defined for all values of $\begin{align*}x\end{align*}$  because the square root of any negative number is not a real number.
      ::yx 没有定义 x 的所有值, 因为任何负数的平方根不是实际数字 。

   

  播放段落

  Section 2.8: Graphical Transformations
  ::第2.8节:图形转换

  播放段落
  1. Reflection across the $\begin{align*}x\end{align*}$ -axis and reflection across the $\begin{align*}y\end{align*}$ -axis.
     ::反射到X轴 反射到Y轴 反射到Y轴
  播放段落
  2. Reflection across the  $\begin{align*}x\end{align*}$ -axis and a horizontal shift left 3 units.
     ::X轴反射和横向移动左倾3个单位。
  播放段落
  3. Horizontal shift left 1 unit and vertical shift down 2 units.
     ::水平向左移动 1 个单位,垂直向下移动 2 个单位。
  播放段落
  4. Reflection across the $\begin{align*}y\end{align*}$ -axis and horizontal shift right 3 units.
     ::反射到Y轴和水平向右3个单位
  播放段落
  5. Reflection across the $\begin{align*}x\end{align*}$ -axis and horizontal compression by a factor of 2.
     ::反射 X 轴和水平压缩的乘数为 2。
  播放段落
  6. Vertical stretch by a factor of 4, horizontal stretch by a factor of 2, and horizontal shift left 2 units.
     ::垂直伸展以4为因数,水平伸展以2为因数,水平移移以2为因数,水平移移以2为单位。
  播放段落
  7. A reflection across the $\begin{align*}x\end{align*}$ -axis, a horizontal shift right 2 units, vertical shift down 2 units, and a vertical stretch by a factor of 3.
     ::X轴反射, 水平向向右移 2 个单位, 垂直向下移 2 个单位, 垂直伸展 3 倍 。
  播放段落
  8. Vertical stretch by a factor of 5 and a horizontal shift left 1 unit.
     ::垂直伸展以5为因数,水平向向向左倾移1个单位。
  播放段落
  9.   $\begin{align*}2h(x-2)+3\end{align*}$  
     ::2h(x-2)+3
  播放段落
  10.   $\begin{align*}\text{-}f(x+2)-1\end{align*}$  
      ::-f(x+2)-2-1
  播放段落
  11.   $\begin{align*}\tfrac{1}{4}g(-x)\end{align*}$  
      ::14g(-x) 14g(-x)
  播放段落
  12.   $\begin{align*}3j(x-2)+3\end{align*}$  
      ::3j(x-2)+3
  播放段落
  13.   $\begin{align*}k(\tfrac{1}{4}(x+1))+3\end{align*}$  
      ::k14( x+1) +3
  播放段落
  14.   $\begin{align*}\tfrac{1}{2}h(\text{-}(x-3))\end{align*}$  
      ::12h(-(x-3)))
  播放段落
  15.   $\begin{align*}\text{-}5f(x)\end{align*}$  
      ::-5f(x)

   

  播放段落

  Section 2.9:  Transforming Functions Defined by Data
  ::第2.9节:数据界定的转换功能

  播放段落
  1. Vertical reflection across the $\begin{align*}x\end{align*}$ -axis, vertical compression by a factor of 2, horizontal shift 1 unit left.
       $\begin{align*}(x,y)\end{align*}$  → ( $\begin{align*}x-1\end{align*}$ , $\begin{align*}-\frac{y}{2}\end{align*}$ )
     
     $\begin{align*}\begin{array}{|c|c|} \hline x & y \\\hline 0 & 5 \\\hline 1 & 6 \\\hline 2 & 7 \\\hline \end{array}\end{align*}$  →  $\begin{align*}\begin{array}{|c|c|} \hline x & y \\\hline \text{-}1 & \text{-}\tfrac{5}{2} \\\hline 0 & \text{-}\tfrac{6}{2} \\\hline 1 & \text{-}\tfrac{7}{2} \\\hline \end{array}\end{align*}$  
     
     ::X轴垂直反射,垂直压缩乘以 2, 水平倾角 1 单位左转。 (x,y) (x-1,-y2) xy051627 Xy-1-520-621-72
  播放段落
  2. Vertical stretch by a factor of 2, horizontal compression by a factor of 3, and vertical shift up 2 units.
       $\begin{align*}(x,y)\end{align*}$  → ( $\begin{align*}\frac{x}{3}\end{align*}$ ,  $\begin{align*}2y+2\end{align*}$ )
     
     $\begin{align*}\begin{array}{|c|c|} \hline x & y \\\hline 0 & 5 \\\hline 1 & 6 \\\hline 2 & 7 \\\hline \end{array}\end{align*}$  →  $\begin{align*}\begin{array}{|c|c|} \hline x & y \\\hline 0 & 12 \\\hline \tfrac{1}{3} & 14 \\\hline \tfrac{2}{3} & 16 \\\hline \end{array}\end{align*}$  
     
     
     ::垂直伸展乘以 2, 垂直伸展乘以 2, 水平压缩乘以 3, 垂直向上移动 2 个单位 。 (x,y) (x3, 2y+2) (x3, 2y+2) × 051627 xy012113142316)
  播放段落
  3. Reflection across the  $\begin{align*}x\end{align*}$ -axis, horizontal shift 4 units to the right, vertical shift 3 units down.
       $\begin{align*}(x,y)\end{align*}$  → ( $\begin{align*}x+4\end{align*}$ , $\begin{align*}-y-3\end{align*}$ )
     
     $\begin{align*}\begin{array}{|c|c|} \hline x & y \\\hline 0 & 5 \\\hline 1 & 6 \\\hline 2 & 7 \\\hline \end{array}\end{align*}$  →  $\begin{align*}\begin{array}{|c|c|} \hline x & y \\\hline 4 & \text{-}8 \\\hline 5 & \text{-}9 \\\hline 6 & \text{-}10 \\\hline \end{array}\end{align*}$  
     
     
     ::反射 x 轴, 水平向向右倾移 4 个单位, 垂直向下移 3 个单位 。 (x, y) (x+4, - y- 3) xy051627 xy4- 85- 96- 10
  播放段落
  4. Vertical stretch by a factor of 3, horizontal compression by a factor of 2, horizontal shift 2 units to the right, and vertical shift up 1 unit.
       $\begin{align*}(x,y)\end{align*}$  → ( $\begin{align*}\frac{x}{2} + 2\end{align*}$ ,  $\begin{align*}3y+1\end{align*}$ )
     
     $\begin{align*}\begin{array}{|c|c|} \hline x & y \\\hline 0 & 5 \\\hline 1 & 6 \\\hline 2 & 7 \\\hline \end{array}\end{align*}$  →  $\begin{align*}\begin{array}{|c|c|} \hline x & y \\\hline 2 & 16 \\\hline 2\tfrac{1}{2} & 19 \\\hline 3 & 22 \\\hline \end{array}\end{align*}$  
     
     
     ::垂直伸展 3 乘以 3, 垂直伸展 3, 水平压缩 以 2 乘以 2 , 向右水平倾斜 2 个单位, 向上垂直向上移 1 个单位 。 (x,y) (x2+2, 3y+1, xy+1) xy051627 xy21621219322
  播放段落
  5. Reflection across the  $\begin{align*}x\end{align*}$ -axis, horizontal shift right 3 units.
       $\begin{align*}(x,y)\end{align*}$  → ( $\begin{align*}x+3\end{align*}$ , $\begin{align*}\text{-}y\end{align*}$ ) 
     
     $\begin{align*}\begin{array}{|c|c|} \hline x & y \\\hline 0 & 5 \\\hline 1 & 6 \\\hline 2 & 7 \\\hline \end{array}\end{align*}$  →  $\begin{align*}\begin{array}{|c|c|} \hline x & y \\\hline 3 & \text{-}5 \\\hline 4 & \text{-}6 \\\hline 5 & \text{-}7 \\\hline \end{array}\end{align*}$  
     
     
     ::X轴反射, 水平向向向右3 个单位。 (x,y) (x+3,-y) xy051627 xy3-54- 65-7
  播放段落
  6.   $\begin{align*}f(x)\end{align*}$  → $\begin{align*}f(2x-6)-4\end{align*}$  
     :xx) f(2x-6)-4
  播放段落
  7.   $\begin{align*}f(x)\end{align*}$ → $\begin{align*}-f(\frac{x}{2}-2)+1\end{align*}$  
     :xx)-(x2-2)+1
  播放段落
  8.   $\begin{align*}f(x)\end{align*}$  →   $\begin{align*}3f(\frac{x}{4})-5\end{align*}$  
     :xx) 3f(x4)-5
  播放段落
  9.   $\begin{align*}f(x)\end{align*}$  → $\begin{align*}-f(\frac{x}{2})+1\end{align*}$  
     :xx)-(x2)+1
  播放段落
  10.   $\begin{align*}f(x)\end{align*}$ →  $\begin{align*}-f(\frac{x}{3})+1\end{align*}$
      
      
      :xx)-(x3)+1
  播放段落
  11.   $\begin{align*}(x,y)\end{align*}$  → ( $\begin{align*}x+2\end{align*}$ , $\begin{align*}3y+1\end{align*}$ )
      :x,y) (x+2, 3y+1)
  播放段落
  12.   $\begin{align*}(x,y)\end{align*}$  → ( $\begin{align*}x+1\end{align*}$ , $\begin{align*}\text{-}4y+3\end{align*}$ )
      :x,y) (x+1,-4y+3)
  播放段落
  13.   $\begin{align*}(x,y)\end{align*}$  → ( $\begin{align*}\frac{x}{2}-1\end{align*}$ ,  $\begin{align*}\frac{y}{2}-5\end{align*}$ )
      :x,y) (x2-1,y2-5)
  播放段落
  14.   $\begin{align*}(x,y)\end{align*}$  → ( $\begin{align*}2x+4\end{align*}$ , $\begin{align*}5y-1\end{align*}$ )
      :x,y) (2x+4,5y-1)
  播放段落
  15.   $\begin{align*}(x,y)\end{align*}$  → ( $\begin{align*}\frac{x}{2}+2\end{align*}$ , $\begin{align*}\frac{y}{4}\end{align*}$ )
      :x,y) (x2+2, y4)

   

  播放段落

  Section 2.10: Asymptotes and End Behavior
  ::第2.10节:小粒子和最终行为

  播放段落
  1. There are no asymptotes. As $\begin{align*}x\end{align*}$  approaches positive infinity, $\begin{align*}y\end{align*}$  approaches positive infinity. As  $\begin{align*}x\end{align*}$  approaches negative infinity, $\begin{align*}y\end{align*}$  approaches negative infinity.
     ::没有微粒。 x 接近正无穷, y 接近正无穷。 x 接近负无穷, y 接近负无穷。
  播放段落
  2. There are no asymptotes. As $\begin{align*}x\end{align*}$  approaches both positive and negative infinity, $\begin{align*}y\end{align*}$   approaches positive infinity.
     ::不存在微粒。 x 既接近正无穷又接近负无穷, y 接近正无穷。
  播放段落
  3. There are no asymptotes. As $\begin{align*}x\end{align*}$  approaches positive infinity, $\begin{align*}y\end{align*}$  approaches positive infinity. As $\begin{align*}x\end{align*}$  approaches negative infinity, $\begin{align*}y\end{align*}$  approaches negative infinity.
     ::没有微粒。 x 接近正无穷, y 接近正无穷。 x 接近负无穷, y 接近负无穷。
  播放段落
  4. There are no asymptotes. As $\begin{align*}x\end{align*}$ approaches positive infinity, $\begin{align*}y\end{align*}$  approaches positive infinity.
     ::没有微量的微量。 x 接近正无穷, y 接近正无穷。
  播放段落
  5. There is a horizontal asymptote at $\begin{align*}y=0\end{align*}$  and a vertical asymptote at  $\begin{align*}x=0\end{align*}$ . As $\begin{align*}x\end{align*}$ approaches both positive and negative infinity, $\begin{align*}y\end{align*}$  approaches 0.
     ::y=0 有水平的同量点, x=0 有垂直的同量点。 x 接近正和负无穷, y 接近0 。
  播放段落
  6. As $\begin{align*}x\end{align*}$  approaches negative infinity, there is a horizontal asymptote at $\begin{align*}y=0\end{align*}$ . As $\begin{align*}x\end{align*}$   approaches positive infinity, $\begin{align*}y\end{align*}$  approaches positive infinity. There is no vertical asymptote.
     ::x 接近负无限度时, y=0 存在水平零点。 x 接近正无穷度时, y 接近正无穷度时, 没有垂直无穷。
  播放段落
  7. There is a vertical asymptote at $\begin{align*}x=0\end{align*}$ . As $\begin{align*}x\end{align*}$  approaches positive infinity, $\begin{align*}y\end{align*}$  approaches positive infinity. As $\begin{align*}x\end{align*}$  approaches 0, $\begin{align*}y\end{align*}$  approaches negative infinity. There is no horizontal asymptote.
     ::x=0 时有一个垂直的无线点。 当 x 接近正无线点时, y 接近正无线点。 x 接近 0 时, y 接近负无线点。 没有水平的无线点 。
  播放段落
  8. As $\begin{align*}x\end{align*}$  approaches negative infinity, there is a horizontal asymptote at $\begin{align*}y=0\end{align*}$ . As $\begin{align*}x\end{align*}$  approaches positive infinity, there is a horizontal asymptote at $\begin{align*}y=1\end{align*}$ . There is no vertical asymptote.
     ::x 接近负无限度时, y= 0 时会出现水平零星。 x 接近正无穷度时, y= 1. 没有垂直无穷。
  播放段落
  9. There is a vertical asymptote at $\begin{align*}x=0\end{align*}$ . As $\begin{align*}x\end{align*}$  approaches positive infinity, there is a horizontal asymptote at $\begin{align*}y=0\end{align*}$ . As $\begin{align*}x\end{align*}$  approaches negative infinity, there is a horizontal asymptote at $\begin{align*}y=2\end{align*}$ .
     ::x=0 时有一个垂直的静态。 x 接近正无穷, y=0 时有一个水平的静态。 x 接近负无穷, y=2 时有一个水平的静态。
  播放段落
  10. There is a vertical asymptote at $\begin{align*}x=1\end{align*}$ . As $\begin{align*}x\end{align*}$  approaches both positive and negative infinity, there is a horizontal asymptote at $\begin{align*}y=2\end{align*}$ .
      ::x=1. x接近正和负无穷时,y=2是水平的无穷状态。
  播放段落
  11. There is a vertical asymptote at $\begin{align*}x=4\end{align*}$ . As $\begin{align*}x\end{align*}$  approaches both positive and negative infinity, there is a horizontal asymptote at $\begin{align*}y=1\end{align*}$ .
      ::x=4. x接近正和负无穷时,y=1是水平的无穷状态。
  播放段落
  12. Because when $\begin{align*}x=0\end{align*}$ ,  $\begin{align*}y=\frac{1}{0},\!\end{align*}$  which is undefined.
      ::因为当 x=0, y=10, 未定义 。
  播放段落
  13. Because when $\begin{align*}x=-3\end{align*}$ ,   $\begin{align*}y=\frac{1}{0},\!\end{align*}$  which is undefined.
      ::因为当 x3, y=10, 未定义时 。
  播放段落
  14.   $\begin{align*}x=2\end{align*}$
      ::x=2x=2
  播放段落
  15.   $\begin{align*}x=\text{-}4\end{align*}$  
      ::x=-4x=-4

   

  播放段落

  Section 2.11: Continuity and Discontinuity
  ::第2.11节:连续性和中断

  播放段落
  1. This function is continuous.
     ::此函数是连续的 。
  播放段落
  2. This function is continuous.
     ::此函数是连续的 。
  播放段落
  3. This function is continuous.
     ::此函数是连续的 。
  播放段落
  4. This function is continuous on its domain.
     ::此函数在其域内是连续的 。
  播放段落
  5. Infinite discontinuity at $\begin{align*}x=0\end{align*}$ .
     ::x=0时无限不连续。
  播放段落
  6. This function is continuous.
     ::此函数是连续的 。
  播放段落
  7. This function is continuous on its domain.
     ::此函数在其域内是连续的 。
  播放段落
  8. This function is continuous.
     ::此函数是连续的 。
  播放段落
  9. There is a removable discontinuity at $\begin{align*}x=\text{-}2\end{align*}$ , infinite discontinuity at $\begin{align*}x=0\end{align*}$ , and a jump discontinuity at $\begin{align*}x=4\end{align*}$ .
     ::x=2时有可移动的不连续状态, x=0时有无限不连续状态, x=4时有跳跃不连续状态。
  播放段落
  10. There is a removable discontinuity at $\begin{align*}x=2\end{align*}$ .
      ::x=2时有可移动的不连续性。
  播放段落
  11. There is a jump discontinuity at $\begin{align*}x=0.3\end{align*}$ .
      ::x=0. 3 时有跳跃不连续状态。
  播放段落
  12. Answers vary, but should show $\begin{align*}f(x)\end{align*}$  has a jump discontinuity at $\begin{align*}x=3\end{align*}$ , a removable discontinuity at $\begin{align*}x=5\end{align*}$ , and another jump discontinuity at $\begin{align*}x=6\end{align*}$ .
      ::答案各有不同,但应显示 f(x) 在 x=3 时有跳跃不连续性, x=5 时有可移动不连续性,而在 x=6 时又有跳跃不连续性。
  播放段落
  13. Answers vary, but should show $\begin{align*}g(x)\end{align*}$ has a jump discontinuity at $\begin{align*}x=\text{-}2\end{align*}$ , an infinite discontinuity at $\begin{align*}x=1\end{align*}$ , and another jump discontinuity at $\begin{align*}x=3\end{align*}$ .
      ::答案不尽相同,但如果显示 g(x) 在 x= 2 时跳跃不连续, 在 x= 1 时无限不连续, 在 x= 3 时再次跳跃不连续, 则显示 g(x) 在 x= 3 时跳跃不连续。
  播放段落
  14. Answers vary, but should show $\begin{align*}h(x)\end{align*}$  has a removable discontinuity at $\begin{align*}x=\text{-}4\end{align*}$ , a jump discontinuity at $\begin{align*}x=1\end{align*}$ , and another jump discontinuity at $\begin{align*}x=7\end{align*}$ .
      ::答案不尽相同,但如果显示 h(x) 在 x= 4 时具有可移动的不连续性, 在 x= 1 时具有跳跃不连续性, 在 x= 7 时则具有另一个跳跃不连续性, 则显示 h(x) 在 x= 7 时具有可移动的不连续性。
  播放段落
  15. Answers vary, but should show $\begin{align*}j(x)\end{align*}$  has an infinite discontinuity at $\begin{align*}x=0\end{align*}$ , a removable discontinuity at $\begin{align*}x=1\end{align*}$ , and a jump discontinuity at  $\begin{align*}x=4\end{align*}$ .
      ::答复各有不同,但应显示j(x)在 x=0 时具有无限不连续性,在 x=1 时具有可移动不连续性,在 x=4 时具有跳跃不连续性。

   

  播放段落

  Section 2.12: Function Combinations and Composition
  ::第2.12节:职能组合和组成

  播放段落
  1. $\begin{align*}g(x) - h(x) = (x-2)^2-3 -(-x) = x^2-3x+1\end{align*}$  
     ::g(x)-h(x)=(x)-2,2-3-(x)=x2-3x+1
  播放段落
  2. $\begin{align*}f(x)=\left|x\right|\end{align*}$  
     
     $\begin{align*}h(x)=\text{-}x\end{align*}$  
     
     $\begin{align*}g(x) = {(x-2)}^{2}-3\end{align*}$  
     
     :xx)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ -\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
  播放段落
  3.   $\begin{align*}f(g(x))=\left|{(x-2)}^{2}-3\right| = \left|x^2-4x+1\right|\end{align*}$
     :g(xx)) (x-2) 2 - 3x2 - 4x+1
  播放段落
  4. The absolute value from $\begin{align*}f(x)\end{align*}$  made all negative $\begin{align*}y\end{align*}$  values for $\begin{align*}g(x)\end{align*}$  positive.
     
     
     ::f( x) 的绝对值使 g( x) 的所有负值为正值。
  播放段落
  5. $\begin{align*}g(f(x))={(\left|x\right|-2)}^{2}-3\end{align*}$  
     ::g(f(x)) = (x%2) 2- 3
  播放段落
  6. Since the absolute value function is even, it created a similar reflection in  $\begin{align*}g(x)\end{align*}$ .
     
     ::由于绝对值函数是偶数,它在 g(x) 中产生了类似的反射。
  播放段落
  7.   $\begin{align*}h(g(x))=\text{-}[(x-2)^2-3] = \text{-}(x-2)^2+3\end{align*}$  
     ::h(g(xx))=-[(x-2)2-2-3]=-(x-2)2+3
  播放段落
  8. The negative from  $\begin{align*}h(x)\end{align*}$  reflects  $\begin{align*}g(x)\end{align*}$  across the  $\begin{align*}x\end{align*}$ -axis.
     
     ::h( x) 的负数反映 X 轴横跨的 g( x) 。
  播放段落
  9.   $\begin{align*}g(h(x))=x^2+4x+1\end{align*}$  
     ::g( h(x)) =x2+4x+1
  播放段落
  10.  The negative from  $\begin{align*}h(x)\end{align*}$  reflects  $\begin{align*}g(x)\end{align*}$  across the  $\begin{align*}y\end{align*}$ -axis. 
      
      ::h( x) 的负数反映 Y 轴对面的 g( x) 。
  播放段落
  11. $\begin{align*}j(x) + m(x) = x^2 + \sqrt{x}\end{align*}$  
      
      ::j(x)+m(x)=x2=x2}x
  播放段落
  12. $\begin{align*}j(x)=x^2\end{align*}$  
      
      $\begin{align*}k(x) = \left|x\right|\end{align*}$  
      
      $\begin{align*}m(x) = \sqrt{x}\end{align*}$  
      
      ::j(x) =x2 k(x) m(x) x
  播放段落
  13. $\begin{align*}j(k(x))={\left|x\right|}^{2}\end{align*}$  
      ::jj(k(x)) x2
  播放段落
  14. Since squaring a number automatically makes it positive, there is no change to the graph of  $\begin{align*}j(x)\end{align*}$ .
      
      ::由于计算数字自动使其呈正数,j(x) 的图形没有变化。
  播放段落
  15.   $\begin{align*}k(m(x))=\left|\sqrt{x}\right|\end{align*}$  
      :km(xx)) x
  播放段落
  16. The graph looks the same as $\begin{align*}m(x)\end{align*}$ .
      
      ::图形看起来与 m( x) 相同 。
  播放段落
  17.   $\begin{align*}m(k(x))=\sqrt{\left|x\right|}\end{align*}$  
      ::m(k(xx)) x
  播放段落
  18. The original square root graph is there, as well as its reflection across the $\begin{align*}y\end{align*}$ -axis. 
      
      ::原始的平方根图就在那里, 以及它在Y轴上的反射。
  播放段落
  19. $\begin{align*}r(p) = 1,\!000-\tfrac{1}{4}(30-25p)^2 = \text{-}156.25p^2+375p+775\end{align*}$  
      :p)=1,000-14(30-25p)2=-156.25p2+375p+775

   

  播放段落

  Section 2.13: Inverses of Functions
  ::第2.13节:职能的反面

  播放段落
  1. $\begin{align*}f(x) = x^3\end{align*}$  
     
     $\begin{align*}f^{\text{-}1}(x) = \sqrt[3]{x}\end{align*}$  
     
     :xx) =x3 f-1 (x) = 3x
  播放段落
  2.   $\begin{align*}f^{\text{-}1}(x)={x}^{\frac{1}{3}} = \sqrt[3]{x}\end{align*}$  
     It is a function.
     ::f-1(x) =x13=3x 这是一个函数 。
  播放段落
  3. 播放段落

       $\begin{align*}f({f}^{-1}(x))={{x}^{\frac{1}{3}}}^{(3)}=x\end{align*}$
     
     ::f( f- 1 (x)) =x13(3) =x

     播放段落

       $\begin{align*}{f}^{-1}(f(x))={{x}^{3}}^{(\frac{1}{3})}=x\end{align*}$   
     
     
     ::-1(f(xx))=x3(13)=x

     
     ::f( f- 1 (x)) =x13(3) =x f- 1 (f(x)) =x3( 13) =x
  播放段落
  4. $\begin{align*}g(x) = \sqrt{x}, \ x \ge 0\end{align*}$  
     
     $\begin{align*}g^{\text{-}1}(x) = x^2, x \ge 0\end{align*}$  
     
     ::g(x) x, x_0 g-1 (x) =x2, x_0
  播放段落
  5.   $\begin{align*}{g}^{\text{-}1}(x)={x}^{2}, x \ge 0\end{align*}$  
     It is a function.
     ::g- (x) =x2, x0, 这是一个函数 。
  播放段落
  6.   $\begin{align*}g({g}^{-1}(x))={(\sqrt{x})}^{2}=x\end{align*}$  
       $\begin{align*}{g}^{-1}(g(x))=\sqrt{{x}^{2}}=x\end{align*}$
     
     
     ::g( g- 1 (x)) = (x) 2=x g- 1 (g(x)) x2=x
  播放段落
  7. $\begin{align*}h(x)=\left|x\right|\end{align*}$  
     
     $\begin{align*}{h}^{\text{-}1}(x)\end{align*}$  
     
     : hx) h-1 (x)
  播放段落
  8. The inverse is $\begin{align*}x=\left|y\right|\end{align*}$  and is not a function.
     ::反之, x
  播放段落
  9. You can see from the graphs that they are inverses because they are symmetrical across the line $\begin{align*}y=x\end{align*}$ .
     ::您可以从图表中看到,它们是反向的,因为它们在横跨y=x线的对称。
  播放段落
  10.   $\begin{align*}j(x)=2x-5\end{align*}$
      
      $\begin{align*}{j}^{\text{-}1}(x)\end{align*}$  
      
      :x)=2x-5j-1(x)
  播放段落
  11.    $\begin{align*}{j}^{-1}(x)=\frac{x+5}{2}\end{align*}$ .
      It is a function.
      ::j- 1(x)=x+52。这是一个函数。
  播放段落
  12.   $\begin{align*}j({j}^{-1}(x))=2(\frac{x+5}{2})-5=x+5-5=x\end{align*}$  
      $\begin{align*}{j}^{-1}(j(x))=\frac{(2x-5)+5}{2}=\frac{2x}{2}=x\end{align*}$  
      ::j(j-1(xx))=2(x+52)=2(x+52)=5=x+5-5=xj-1(j(x))=(2x-5)+52=2x2=x
  播放段落
  13. The inverse is not a function since the function doesn't pass the horizontal line test.
      
      ::反向不是一个函数, 因为函数不会通过水平线测试 。
  播放段落
  14. No. The inverse of  $\begin{align*}g(x)\end{align*}$  is  $\begin{align*}{g}^{-1}(x)={e}^{x}-1\end{align*}$ .
      ::否。 g(x) 的反义值是 g- 1(x) =ex- 1 。
  播放段落
  15. You could switch the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -coordinates given in the original table to make the table for the inverse.
      ::您可以切换原表格中给定的 x 和 Y 坐标, 使表格为反向 。
  播放段落
  16. a. F(0) = 9/5(0) + 32 = 32; F(100) = 9/5(100)+32 = 212
      b. C(F) = (F-32)*5/9
      c. F(C(F) = 9/5((F-32)*5/9) + 32 = F and C(F(C)) = ((9/5C+32)-32)*5/9
      ::F(0)=9/5(0)+32=32;F(100)=9/5(100)+32=9/5(100)+32=212b.C(F)=(F-32)*5/9c.F(C(F)=9/5((F-32)*5/9)+32=F和C(F(C))=(9/5C+32-32)*5/9