Blender 3D:各种各样的教程

In  optics ,  Lambert's cosine law  says that the observed  radiant intensity  or  luminous intensity  from an ideal  diffusely reflecting  surface or ideal diffuse radiator is  directly proportional  to the  cosine  of the angle  θ  between the observer's line of sight and the  surface normal ;  I  =  I ₀  cos  θ . ^{[1] [2]}  The law is also known as the  cosine emission law ^[3]  or  Lambert's emission law . It is named after  Johann Heinrich Lambert , from his  Photometria , published in 1760. ^[4]
::在光学中,兰伯特的共弦定律说,从理想的分散反射表面或理想的分散散热器观察到的辐射强度或光强度与观察者的视线与表面正常之间的角度 θ 的共弦正比; I = I0 cos θ . [1] [2] 该定律也被称为共弦发射定律 [3] 或兰伯特的发射定律.它以约翰·海因里希·兰伯特的名字命名,来自于他在1760年出版的"光度学" (Photometria). [4]

A surface which obeys Lambert's law is said to be  Lambertian , and exhibits  Lambertian reflectance . Such a surface has a constant  radiance / luminance , regardless of the angle from which it is observed; a single human eye perceives such a surface as having a constant brightness, regardless of the angle from which the eye observes the surface. It has the same radiance because, although the emitted power from a given area element is reduced by the cosine of the emission angle, the solid angle, subtended by surface visible to the viewer, is reduced by the very same amount. Because the ratio between power and solid angle is constant, radiance (power per unit solid angle per unit projected source area) stays the same.
::遵守兰伯特定律的表面被称为兰伯特表面,并且具有兰伯特反射.这样的表面具有恒定的辐射/发光度,无论从何角度观察;单一的人类眼睛认为这样的表面具有恒定的亮度,无论从何角度观察表面.它具有相同的辐射,因为尽管从给定的区域元素发出的功率减少了辐射角度的共弦值,但对观众可见的表面加微的固体角度减少了相同的数量.由于功率和固体角度之间的比率是恒定的,辐射 (功率每单位固体角度每单位投射源区域) 保持不变.

When an area element is radiating as a result of being illuminated by an external source, the  irradiance  (energy or photons /time/area) landing on that area element will be proportional to the cosine of the angle between the illuminating source and the normal. A Lambertian scatterer will then scatter this light according to the same cosine law as a Lambertian emitter. This means that although the radiance of the surface depends on the angle from the normal to the illuminating source, it will not depend on the angle from the normal to the observer. For example, if the  moon  were a Lambertian scatterer, one would expect to see its scattered brightness appreciably diminish towards the  terminator  due to the increased angle at which sunlight hit the surface. The fact that it does not diminish illustrates that the moon is not a Lambertian scatterer, and in fact tends to scatter more light into the  oblique angles  than a Lambertian scatterer.
::当一个区域元素因被外部源照射而辐射时,该区域元素上的辐射 (能量或光子/时间/区域) 将与照射源与正常之间的角度的等比相对应.兰伯特散射器将根据兰伯特发射器相同的等比定律散射这种光.这意味着,虽然表面的辐射取决于从正常到照射源的角度,但它不会取决于从正常到观察者的角度.例如,如果月球是一个兰伯特散射器,人们会期待看到它的散射亮度明显减少到终点因太阳光撞击表面的角度增加.它没有减少说明月球不是兰伯特散射器,事实上,光往往散射到更的角度比兰伯特散射器.

The emission of a Lambertian radiator does not depend on the amount of incident radiation, but rather from radiation originating in the emitting body itself. For example, if the  sun  were a Lambertian radiator, one would expect to see a constant brightness across the entire solar disc. The fact that the sun exhibits  limb darkening  in the visible region illustrates that it is not a Lambertian radiator. A  black body  is an example of a Lambertian radiator.
::兰伯特辐射器的辐射并不取决于发生辐射的量,而是取决于发射物本身的辐射.例如,如果太阳是兰伯特辐射器,人们会期望在整个太阳盘中看到恒定的亮度.太阳在可见区域呈现肢体变暗的事实说明它不是兰伯特辐射器.黑体是兰伯特辐射器的一个例子.

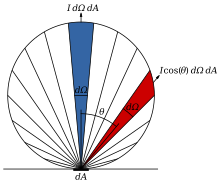
The situation for a Lambertian surface (emitting or scattering) is illustrated in Figures 1 and 2. For conceptual clarity we will think in terms of  photons  rather than  energy  or  luminous energy . The wedges in the  circle  each represent an equal angle  d Ω, of an arbitrarily chosen size, and for a Lambertian surface, the number of photons per second emitted into each wedge is proportional to the area of the wedge.
::兰伯特表面 (发射或散射) 的情况如图1和图2所示.为了概念的清晰,我们将用光子来思考,而不是能量或光能.圆中的形每个代表一个等角的dΩ,任意选择大小,对于兰伯特表面,每秒发射到每个形中的光子数量与形的面积成比例.

The length of each wedge is the product of the  diameter  of the circle and cos( θ ). The maximum rate of photon emission per unit  solid angle  is along the normal, and diminishes to zero for  θ  = 90°. In mathematical terms, the  radiance  along the normal is  I  photons/(s·m ² ·sr) and the number of photons per second emitted into the vertical wedge is  I   d Ω  dA . The number of photons per second emitted into the wedge at angle  θ  is  I  cos( θ )  d Ω  dA .
::每个的长度是圆的直径和cos{\displaystyle \mathbb {c} }θ 的乘积.每单位固角的光子发射的最大速率沿着正则,并且在θ=90°时减为零.用数学术语来说,沿着正则的辐射量是I光子/{\displaystyle \mathbb {s} }s2{\displaystyle \mathbb {s} }sr) ,而每秒发射到垂直的光子数量是IdΩ dA.在角 θ时,每秒发射到的光子数量是I cos{\displaystyle \mathbb {s} }θ) dΩ dA.

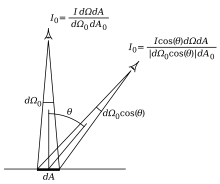
Figure 2 represents what an observer sees. The observer directly above the area element will be seeing the scene through an aperture of area  dA ₀  and the area element  dA  will subtend a (solid) angle of  d Ω ₀ , which is a portion of the observer's total angular field-of-view of the scene. Since the wedge size  d Ω was chosen arbitrarily, for convenience we may assume without loss of generality that it coincides with the solid angle subtended by the aperture when "viewed" from the locus of the emitting area element dA. Thus the normal observer will then be recording the same  I   d Ω  dA  photons per second emission derived above and will measure a radiance of
::图2表示观察者所看到的. 直接在面积元素之上的观察者将通过面积dA0的光圈看到场景,而面积元素dA将承载一个 (固体) 角度dΩ0,这是观察者对场景的总角度视野的一部分. 由于形尺寸dΩ是任意选择的,为了方便,我们可以在不损失一般性的情况下假定它与从发射面积元素dA的位置"观看"时,由光圈所承载的固体角度相吻合. 因此,正常将记录相同的I dΩ dA光子每秒发射,并将测量

${\displaystyle I_0=\frac{Id\mathrm{\Omega }dA}{d{\mathrm{\Omega }}_{0}d{A}_0}}$  photons/(s·m ² ·sr).

The observer at angle  θ  to the normal will be seeing the scene through the same aperture of area  dA ₀  (still corresponding to a  d Ω wedge) and from this oblique vantage the area element  dA  is foreshortened and will subtend a (solid) angle of  d Ω ₀  cos( θ ). This observer will be recording  I  cos( θ )  d Ω  dA  photons per second, and so will be measuring a radiance of
::在角 θ 与正常的观察者将通过相同的面积 dA0 的光圈看到场景 (仍然对应于 dΩ ),从这个斜视角,面积元素 dA 缩短,并将延伸 dΩ0 cos ((θ) 的 (固态) 角度. 这个观察者将记录每秒 I cos ((θ) dΩ dA 光子,因此将测量出

${\displaystyle I_0=\frac{I\cos (\theta )d\mathrm{\Omega }dA}{d{\mathrm{\Omega }}_0\cos (\theta )d{A}_0}=\frac{Id\mathrm{\Omega }dA}{d{\mathrm{\Omega }}_{0}d{A}_0}}$  photons/(s·m ² ·sr),

which is the same as the normal observer.
::这与正常观察者相同.

In general, the  luminous intensity  of a point on a surface varies by direction; for a Lambertian surface, that distribution is defined by the cosine law, with peak luminous intensity in the normal direction. Thus when the Lambertian assumption holds, we can calculate the total  luminous flux ,  ${\displaystyle F_{\text{tot}}}$ , from the peak  luminous intensity ,  ${\displaystyle I_{max}}$ , by integrating the cosine law: and so
::一般来说,表面上的点的光强度因方向而异;对于兰伯特表面,该分布是由共弦定律定义的,峰值光强度在正常方向.因此,当兰伯特假设成立时,我们可以通过整合共弦定律来计算总光流,F tot,从峰值光强度,I max:F tot = ∫ 0 2 π ∫ 0 π / 2 cos (θ ) I max sin (θ ) d θ d φ = 2 π ⋅ I max ∫ 0 π / 2 cos (θ ) sin (θ ) d θ = 2 π ⋅ I max ∫ 0 π / 2 cos (θ ) sin (θ ) d θ = 2 π ⋅ I max ∫ 0 π / 2 sin (θ 2) d θ 等

${\displaystyle F_{\text{tot}}=\pi \mathrm{s}\mathrm{r}\cdot I_{max}}$

where  ${\displaystyle \sin (\theta )}$  is the determinant of the  Jacobian matrix  for the  unit sphere , and realizing that  ${\displaystyle I_{max}}$  is luminous flux per  steradian . ^[5]  Similarly, the peak intensity will be  ${\displaystyle 1/(\pi \mathrm{s}\mathrm{r})}$  of the total radiated luminous flux. For Lambertian surfaces, the same factor of  ${\displaystyle \pi \mathrm{s}\mathrm{r}}$  relates  luminance  to  luminous emittance ,  radiant intensity  to  radiant flux , and  radiance  to  radiant emittance . ^{[ citation needed ]}  Radians and steradians are, of course, dimensionless and so "rad" and "sr" are included only for clarity.
::在这里,sin (θ ) 是单位球的雅可比矩阵的决定数,并意识到I max是每斯特拉第安的光流. [1] 同样,峰值强度将是总辐射光流的1/ (π s r).对于兰伯特表面,相同的π s r因子与发光率,辐射强度与辐射流,辐射到辐射发光率有关. 辐射和斯特拉第安当然是无维的,因此"rad"和"sr"仅用于清晰度.

Example: A surface with a luminance of say 100 cd/m ²  (= 100 nits, typical PC monitor) will, if it is a perfect Lambert emitter, have a luminous emittance of 100π lm/m ² . If its area is 0.1 m ²  (~19" monitor) then the total light emitted, or luminous flux, would thus be 31.4 lm.
::例如:一个表面的发光率为100 cd/m2 (=100 nits,典型的PC显示器),如果它是一个完美的兰伯特发射器,则具有100π lm/m2的发光率.如果它的面积为0.1 m2 (~19"显示器),则发射的总光量或光流将是31.4 lm.