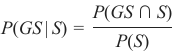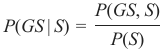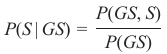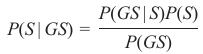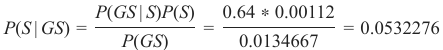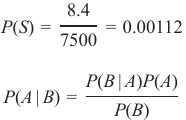Scikit朴素贝叶斯分类器(Naive Bayes Classifier with Scikit)
章节大纲
-
定义

在机器学习中,贝叶斯分类器是一种简单的概率分类器,其基础是应用贝叶斯定理。朴素贝叶斯分类器使用的特征模型做出了强独立性假设。这意味着某个类别特定特征的存在与任何其他特征的存在是独立或不相关的。
独立事件的定义:
如果事件 E 和 F 都具有正概率,并且 且 ,则事件 E 和 F 是独立的。
正如我们在定义中所述,朴素贝叶斯分类器基于贝叶斯定理。贝叶斯定理基于条件概率,我们现在将定义它:
条件概率
P(A∣B) 代表“在 B 发生的条件下 A 的条件概率”,或“在条件 B 下 A 的概率”,即在事件 B 发生的前提下,某个事件 A 发生的概率。当在随机实验中已知事件 B 已经发生时,实验的可能结果就减少到 B,因此 A 发生的概率从无条件概率变为在给定 B 条件下的条件概率。联合概率是两个事件同时发生的概率。也就是说,它是两个事件一起发生的概率。A 和 B 的联合概率有三种表示法,可以写成:
-
-
P(AB)
-
P(A,B)
条件概率定义为:
条件概率的例子
讲德语的瑞士人
瑞士约有 840 万人口。其中约 64% 讲德语。地球上约有 75 亿人口。
如果外星人随机传送一个地球人上来,他是讲德语的瑞士人的几率是多少?
我们有以下事件:
S: 成为瑞士人
GS: 讲德语
随机选择一个人是瑞士人的概率:
如果我们知道某人是瑞士人,那么他讲德语的概率是 0.64。这对应于条件概率:
所以地球人是瑞士人并且讲德语的概率可以通过以下公式计算:
代入上述值,我们得到:
从而得到:
所以我们的外星人选中一个讲德语的瑞士人的几率是 0.07168%。
假阳性和假阴性
一个医学研究实验室提议对一大群人进行疾病筛查。反对这种筛查的一个论点是假阳性筛查结果的问题。
假设这组人中有 0.1% 患有该疾病,其余人健康:
和
对于筛查测试,以下情况属实:
如果您患有该疾病,测试将有 99% 的时间呈阳性;如果您没有患病,测试将有 99% 的时间呈阴性:
和
最后,假设当测试应用于患有该疾病的人时,有 1% 的几率出现假阴性结果(和 99% 的几率获得真阳性结果),即:
和
患病
健康
总计
测试结果阳性
99
999
1098
测试结果阴性
1
98901
98902
总计
100
99900
100000
有 999 个假阳性和 1 个假阴性。
问题:
在许多情况下,即使是医疗专业人员也认为“如果你患有这种疾病,测试将在 99% 的时间里呈阳性;如果你没有患病,测试将在 99% 的时间里呈阴性”。在报告阳性结果的 1098 个案例中,只有 99 个(9%)是正确的,而 999 个案例是假阳性(91%),即如果一个人得到阳性测试结果,他或她实际患有该疾病的概率只有大约 9%。
贝叶斯定理
我们计算了条件概率 P(GS∣S),即已知某人是瑞士人的情况下,他或她讲德语的概率。为了计算这个,我们使用了以下等式:
那么计算 P(S∣GS) 又如何呢?即在已知某人讲德语的情况下,他是瑞士人的概率是多少?
这个等式看起来像这样:
让我们在两个等式中都孤立出 P(GS,S):
P(GS,S)=P(GS∣S)P(S)
P(GS,S)=P(S∣GS)P(GS)
由于左侧相等,右侧也必须相等:
这个等式可以转化为:
这个结果对应于贝叶斯定理。
要解决我们的问题——即已知某人讲德语的情况下,他是瑞士人的概率——我们只需计算右侧。我们已经从之前的练习中得知:
和
世界上讲德语的母语者人数约为 1.01 亿,所以我们知道:
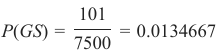
最后,我们可以通过将值代入我们的等式来计算 P(S∣GS):
瑞士约有 840 万人口。其中约 64% 讲德语。地球上约有 75 亿人口。
如果外星人随机传送一个地球人上来,他是讲德语的瑞士人的几率是多少?
我们有以下事件:
S: 成为瑞士人 GS: 讲德语
P(A∣B) 是在给定 B 的条件下 A 的条件概率(后验概率),P(B) 是 B 的先验概率,P(A) 是 A 的先验概率。P(B∣A) 是在给定 A 的条件下 B 的条件概率,称为似然。
朴素贝叶斯分类器的一个优点是,它只需要少量训练数据即可估计分类所需的参数。由于假设变量是独立的,因此只需要确定每个类别的变量方差,而不需要确定整个协方差矩阵。
DEFINITION
In machine learning, a Bayes classifier is a simple probabilistic
classifier, which is based on applying Bayes' theorem. The
feature model used by a naive Bayes classifier makes strong
independence assumptions. This means that the existence of a
particular feature of a class is independent or unrelated to the
existence of every other feature.
Definition of independent events:
Two events E and F are independent, if both E and F have
positive probability and if P(E|F) = P(E) and P(F|E) = P(F)
As we have stated in our definition, the Naive Bayes Classifier
is based on the Bayes' theorem. The Bayes theorem is based on
the conditional probability, which we will define now:
CONDITIONAL PROBABILITY
P(A | B) stands for "the conditional probability of A given B", or "the probability of A under the condition B",
i.e. the probability of some event A under the assumption that the event B took place. When in a random
experiment the event B is known to have occurred, the possible outcomes of the experiment are reduced to B,
and hence the probability of the occurrence of A is changed from the unconditional probability into the
conditional probability given B. The Joint probability is the probability of two events in conjunction. That is, it
is the probability of both events together. There are three notations for the joint probability of A and B. It can
be written as
•••P(A ∩ B)
P(AB) or
P(A, B)
The conditional probability is defined by
P(A ∩ B)
P(A | B) =
P(B)
EXAMPLES FOR CONDITIONAL PROBABILITY
GERMAN SWISS SPEAKER
There are about 8.4 million people living in Switzerland. About 64 % of them speak German. There are about
300
7500 million people on earth.
If some aliens randomly beam up an earthling, what are the chances that he is a German speaking Swiss?
We have the events
S: being Swiss
GS: German Speaking
The probability for a randomly chosen person to be Swiss:
8.4
P(S) =
= 0.00112
7500
If we know that somebody is Swiss, the probability of speaking German is 0.64. This corresponds to the
conditional probability
P(GS | S) = 0.64
So the probability of the earthling being Swiss and speaking German, can be calculated by the formula:
P(GS ∩ S)
P(GS | S) =
P(S)
inserting the values from above gives us:
P(GS ∩ S)
0.64 =
0.00112
and
P(GS ∩ S) = 0.0007168
So our aliens end up with a chance of 0.07168 % of getting a German speaking Swiss person.
FALSE POSITIVES AND FALSE NEGATIVES
A medical research lab proposes a screening to test a large group of people for a disease. An argument against
such screenings is the problem of false positive screening results.
Suppose 0,1% of the group suffer from the disease, and the rest is well:
P( " sick " ) = 0, 1
and
301
P( " well " ) = 99, 9
The following is true for a screening test:
If you have the disease, the test will be positive 99% of the time, and if you don't have it, the test will be
negative 99% of the time:
P("test positive" | "well") = 1 %
and
P("test negative" | "well") = 99 %.
Finally, suppose that when the test is applied to a person having the disease, there is a 1% chance of a false
negative result (and 99% chance of getting a true positive result), i.e.
P("test negative" | "sick") = 1 %
and
P("test positive" | "sick") = 99 %
Sick
Healthy
Totals
Test result positive
99
999
1098
Test result
1
98901
98902
negative
Totals
100
99900
100000
There are 999 False Positives and 1 False Negative.
Problem:
In many cases even medical professionals assume that "if you have this sickness, the test will be positive in 99
% of the time and if you don't have it, the test will be negative 99 % of the time. Out of the 1098 cases that
report positive results only 99 (9 %) cases are correct and 999 cases are false positives (91 %), i.e. if a person
gets a positive test result, the probability that he or she actually has the disease is just about 9 %. P("sick" |
"test positive") = 99 / 1098 = 9.02 %
BAYES' THEOREM
We calculated the conditional probability P(GS | S), which was the probability that a person speaks German, if
302
he or she is known to be Swiss. To calculate this we used the following equation:
P(GS, S)
P(GS | S) =
P(S)
What about calculating the probability P(S | GS), i.e. the probability that somebody is Swiss under the
assumption that the person speeks German?
The equation looks like this:
P(GS, S)
P(S | GS) =
P(GS)
Let's isolate on both equations P(GS, S):
P(GS, S) = P(GS | S)P(S)
P(GS, S) = P(S | GS)P(GS)
As the left sides are equal, the right sides have to be equal as well:
P(GS | S) ∗ P(S) = P(S | GS)P(GS)
This equation can be transformed into:
P(GS | S)P(S)
P(S | GS) =
P(GS)
The result corresponts to Bayes' theorem
To solve our problem, - i.e. the probability that a person is Swiss, if we know that he or she speaks German -
all we have to do is calculate the right side. We know already from our previous exercise that
P(GS | S) = 0.64
and
P(S) = 0.00112
The number of German native speakers in the world corresponds to 101 millions, so we know that
101
P(GS) =
= 0.0134667
7500
Finally, we can calculate P(S | GS) by substituting the values in our equation:
P(GS | S)P(S)
0.64 ∗ 0.00112
P(S | GS) =
=
= 0.0532276
P(GS)
0.0134667
303
There are about 8.4 million people living in Switzerland. About 64 % of them speak German. There are about
7500 million people on earth.
If the some aliens randomly beam up an earthling, what are the chances that he is a German speaking Swiss?
We have the events
S: being Swiss GS: German Speaking
8.4
P(S) =
= 0.00112
7500
P(B | A)P(A)
P(A | B) =
P(B)
P(A | B) is the conditional probability of A, given B (posterior probability), P(B) is the prior probability of B
and P(A) the prior probability of A. P(B | A) is the conditional probability of B given A, called the likely-hood.
An advantage of the naive Bayes classifier is that it requires only a small amount of training data to estimate
the parameters necessary for classification. Because independent variables are assumed, only the variances of
the variables for each class need to be determined and not the entire covariance matrix. -